▷ Производная тангенса (формула и решенные упражнения)

Здесь вы узнаете, как получается функция тангенса. Кроме того, вы сможете увидеть примеры производной касательной и даже потренироваться, решая упражнения шаг за шагом. Наконец, мы также продемонстрируем формулу производной тангенса и покажем вам формулу производной обратного тангенса.

Что является производной тангенса?

Производная тангенса x равна 1 по квадрату косинуса x. Производная тангенса x также эквивалентна квадрату секущего x и 1 плюс квадрат тангенса x.

$\begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}$

Все выражения эквивалентны, поэтому для получения функции тангенса есть три возможные формулы.

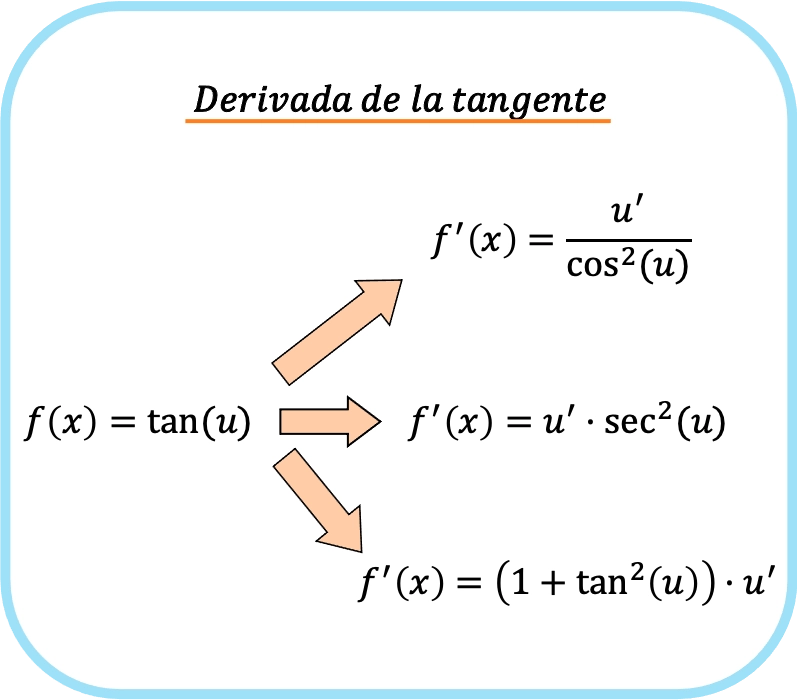
С другой стороны, когда в аргументе касательной у нас есть функция, отличная от x (назовем ее u), мы должны применить правило цепочки. Таким образом, производная тангенса u равна:

$\begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}$

Вкратце правило касательной производной можно резюмировать следующим образом:

Примеры касательной производной

Учитывая формулу производной тангенса, в этом разделе мы решим несколько примеров тригонометрических производных этого типа, чтобы вы поняли, как вывести функцию тангенса.

Пример 1: Производная тангенса 2x

$f(x)=\text{tan}(2x)$

Чтобы вычислить производную тангенса, вы можете использовать одну из трех формул, которые мы видели выше. В данном случае воспользуемся формулой косинуса:

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

Функция 2x линейна, поэтому ее производная равна 2. Таким образом, производная тангенса 2x равна 2 по квадрату косинуса 2x:

$f(x)=\text{tan}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cos}^2(2x)}$

Пример 2: Производная тангенса x в квадрате

$f(x)=\text{tan}(x^2)$

В этом примере функция касательного аргумента — это не x, а функция с производной. Это означает, что нам нужно применить правило цепочки, чтобы получить его.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

Производная x в квадрате равна 2x, поэтому производная тангенса x ² равна:

$f(x)=\text{tan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cos}^2(x^2)}$

Пример 3: Производная касательной к кубу

$f(x)=\text{tan}^3(9x^2-4x)$

В этой задаче у нас есть составная функция, поэтому нам также нужно будет использовать правило цепочки, чтобы дифференцировать касательную.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

Кроме того, тангенс возводится в степень 3, а это значит, что перед применением формулы производной тангенса необходимо воспользоваться формулой производной степени:

$\begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}$

Производная обратного тангенса

Как и любая обратная функция, функция тангенса также имеет обратную функцию — арктангенс. Хотя формула для ее получения не похожа на формулу тангенса, мы показываем ее вам, поскольку в некоторых случаях она может быть полезна.

Производная обратного тангенса функции представляет собой частное деления производной функции на единицу плюс квадрат указанной функции.

$f(x)=\text{tan}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

Например, производная обратного тангенса 3х равна:

$f(x)=\text{tan}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{1+(3x)^2}=\cfrac{3}{1+9x^2}$

Решенные упражнения на производную тангенса

Вычислите производную следующих касательных функций:

$\text{A) } f(x)=\text{tan}(3x)$

$\text{B) } f(x)=\text{tan}(x^3-10x^2+8)$

$\text{C) } \displaystyle f(x)=\text{tan}^2\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{tan}\left(e^{2x}\right)$

$\text{E) } f(x)=\text{tan}\bigl(\ln(4x)\bigr)$

$\text{F) } f(x)=\text{tan}\left(\sqrt{3x}\right)$

Посмотреть решение

$\text{A) } f'(x)=\cfrac{3}{\text{cos}^2(3x)}$

$\text{B) } f'(x)=\cfrac{3x^2-20x}{\text{cos}^2(x^3-10x^2+8)}$

$\text{C) } \displaystyle f'(x)=2\text{tan}\left(\frac{x}{2}\right)\cdot \frac{1}{\text{cos}^2\left(\frac{x}{2}\right)}\cdot \frac{1}{2}=\frac{\text{tan}\left(\frac{x}{2}\right)}{\text{cos}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=\cfrac{2e^{2x}}{\text{cos}^2(e^{2x})}$

$\text{E) } f'(x)=\cfrac{\frac{4}{4x}}{\text{cos}^2\bigl(\ln(4x)\bigr)}=\cfrac{1}{x\cdot\text{cos}^2\bigl(\ln(4x)\bigr)}$

$\text{F) } f'(x)=\cfrac{\frac{3}{2\sqrt{3x}}}{\text{cos}^2\left(\sqrt{3x}\right)}=\cfrac{3}{2\sqrt{3x}\cdot \text{cos}^2\left(\sqrt{3x}\right)}$

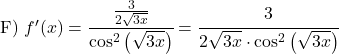
Доказательство производной тангенса

Чтобы вы могли убедиться, что это не выдуманное выражение, в этом разделе мы продемонстрируем формулу производной тангенса, используя математическое определение тангенса.

Для этого начнем с тригонометрического тождества, связывающего три тригонометрических отношения:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

Если мы воспользуемся формулой производной от деления , то производная будет иметь вид:

$\displaystyle\left(\text{tan}(x)\right)'=\left(\frac{\text{sen}(x)}{\text{cos}(x)}\right)'$

$\text{tan}'(x)=\cfrac{\text{cos}(x)\cdot \text{cos}(x)+\text{sen}(x)\text{sen}(x) }{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

Но, используя фундаментальное тригонометрическое тождество, мы знаем, что квадрат синуса плюс квадрат косинуса равен 1:

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{tan}'(x)=\cfrac{1}{\text{cos}^2(x)}$

И вот мы уже пришли к первой формуле производной тангенса. Более того, секущая является мультипликативной обратной косинусу, поэтому выводится и второе выражение:

$\text{tan}'(x)=\text{sec}^2(x)$

Наконец, третье правило касательной производной можно доказать, превратив дробь из предыдущего шага в сумму дробей:

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)}{\text{cos}^2(x)}+\cfrac{\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=1+\text{tan}^2(x)$

Что является производной тангенса?

Примеры касательной производной

Пример 1: Производная тангенса 2x

Пример 2: Производная тангенса x в квадрате

Пример 3: Производная касательной к кубу

Производная обратного тангенса

Решенные упражнения на производную тангенса

Доказательство производной тангенса

Оставьте комментарий Отменить ответ