Образовано от корня

Здесь мы объясним, как взять производную корня (или радикальной функции). Вы найдете формулу деления корней и пошагово решенные упражнения для производных корней.

Формула производной корня

Производная корня, или иррациональная функция, равна производной подкоренного выражения (выражение под радикалом), разделенной на произведение индекса корня, умноженного на тот же корень, путем вычитания 1 из показателя подкоренного выражения.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Однако если корневым подкоренным выражением является просто x, формулы упрощаются. Таким образом, корневая производная x равна следующему:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Короче говоря, есть две формулы для получения корня: первую можно использовать всегда, а вторую можно использовать только тогда, когда подкоренное выражение равно х.

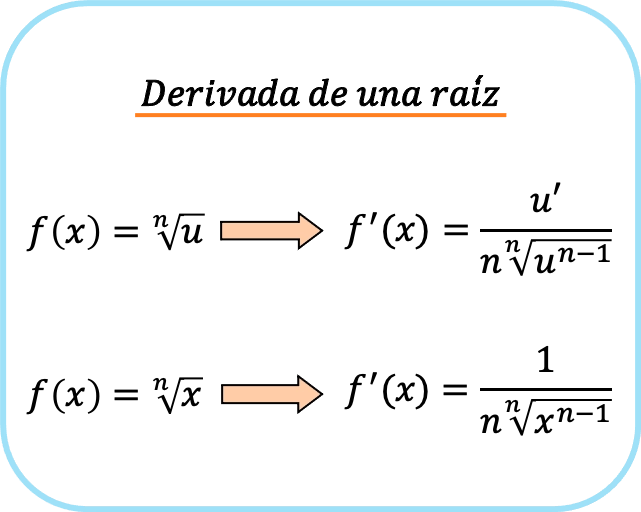
Если присмотреться, то в числителе дроби стоит тот самый член, который получается в результате применения правила цепочки при взятии производной от корня. Вот почему, когда подкоренное выражение равно x, в знаменателе появляется 1, поскольку это производная от x.

Примеры корневых производных

Учитывая формулу производной радикальной функции, ниже мы объясним несколько примеров производной этого типа, чтобы вы поняли, как взять производную от корня.

Пример 1: Производная квадратного корня

Затем мы увидим, что такое производная квадратного корня:

$f(x)=\sqrt{x}$

В этом случае выражение внутри корня — это просто x, поэтому мы можем использовать следующую формулу:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Таким образом, производная квадратного корня равна 1, разделенному на произведение 2-кратного квадратного корня из x:

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

Пример 2: Производная кубического корня

$f(x)=\sqrt[3]{x}$

В этом примере выражение под корнем — это x, поэтому мы можем применить следующую формулу:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Таким образом, производная кубического корня равна 1, разделенному на 3-кратный кубический корень из x в квадрате:

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

Пример 3: Производная корня четвертой степени

$f(x)=\sqrt[4]{7x-2}$

Теперь у нас нет х под знаком радикала, но у нас есть более сложное алгебраическое выражение. Поэтому надо воспользоваться общей формулой производной корня:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Выражение под радикалом является функцией первой степени, поэтому его производная равна 7. Таким образом, производная всей функции равна:

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

Пример 4: Вывод от одного корня к другому

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

Чтобы решить производную этого корня, составленную из другого корня, мы должны применить следующую формулу:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

В этом случае для вычисления производной необходимо дважды подряд использовать одну и ту же формулу:

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

Решенные задачи о производной корня

Вычислите производные следующих корней:

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

посмотреть решение

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

Произведено от корня

Формула производной корня

Примеры корневых производных

Пример 1: Производная квадратного корня

Пример 2: Производная кубического корня

Пример 3: Производная корня четвертой степени

Пример 4: Вывод от одного корня к другому

Решенные задачи о производной корня

Оставьте комментарий Отменить ответ