Производная гиперболического тангенса

Здесь вы узнаете, чему равна производная гиперболического тангенса функции. Кроме того, вы сможете увидеть несколько решенных примеров производных гиперболических тангенсов. И, наконец, мы покажем вам формулу производной гиперболического тангенса.

Формула производной гиперболического тангенса

Производная гиперболического тангенса x равна 1, деленной на квадрат гиперболического косинуса x. Производная тангенса x также эквивалентна квадрату гиперболического секущего x и 1 минус квадрат гиперболического тангенса x.

$\begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}$

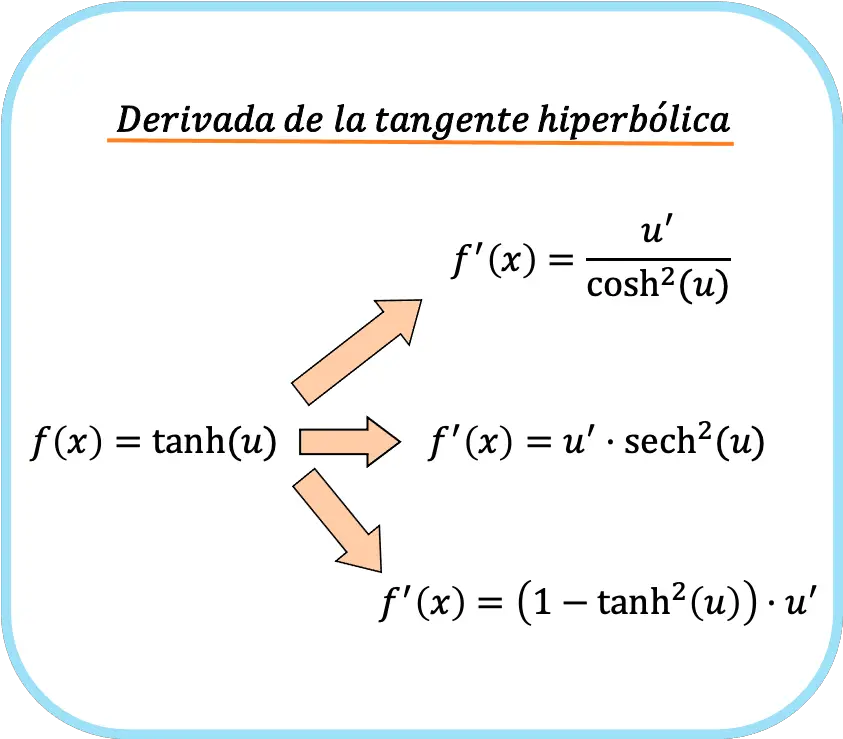
С другой стороны, если в аргументе функции у нас есть функция, отличная от x, мы должны применить правило цепочки. И тогда три формулы для производной гиперболического тангенса:

$\begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}$

Это не означает, что каждый раз, когда мы получаем гиперболический тангенс, мы должны использовать все три формулы, а скорее то, что мы можем использовать любую из них для его получения. Итак, в зависимости от функции аргумента гиперболического тангенса лучше будет использовать ту или иную формулу. Ниже приведены несколько примеров, на которых вы можете увидеть, как получается гиперболический тангенс функции.

Производная гиперболического тангенса почти идентична производной тангенса, но имеет небольшую деталь, которая делает их совершенно разными. Посмотреть, в чем разница, можно по следующей ссылке:

➤ См. формулу производной касательной.

Примеры производной гиперболического тангенса

Увидев, какова формула производной гиперболического тангенса, вот несколько примеров решения производных тригонометрических функций этого типа, чтобы вы полностью поняли, как вывести гиперболический тангенс.

Пример 1: Производная гиперболического тангенса 2x

$f(x)=\text{tanh}(2x)$

Чтобы получить гиперболический тангенс в этом примере, мы будем использовать формулу гиперболического косинуса, хотя вы, конечно, можете использовать любую, которую предпочитаете.

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

Мы знаем, что производная 2x равна 2, поэтому производная всей функции равна:

$f(x)=\text{tanh}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cosh}^2(2x)}$

Пример 2: Производная гиперболического тангенса x в квадрате

$f(x)=\text{tanh}(x^2)$

Правило для производной гиперболического тангенса функции:

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

С одной стороны, мы дифференцируем функцию от аргумента x ² , что дает 2x, а затем находим производную всей функции по формуле:

$f(x)=\text{tanh}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cosh}^2(x^2)}$

Пример 3: Производная гиперболического тангенса в кубе

$f(x)=\text{tanh}^3(7x^2)$

В этом случае нам необходимо вывести гиперболический тангенс функции, к тому же возведенной в степень. Значит нам нужно воспользоваться формулой производной потенциальной функции, правилом производной гиперболического тангенса и цепным правилом:

$f'(x)=3\text{tanh}^2(7x^2)\cdot \cfrac{14x}{\text{cosh}^2(7x^2)}}=\cfrac{42x\cdot \text{tanh}^2(7x^2)}{\text{cosh}^2(7x^2)}}$

Доказательство производной тангенса

В этом разделе мы продемонстрируем формулу для производной гиперболического тангенса. И для этого мы начнем с тригонометрического тождества, которое связывает три гиперболических тригонометрических отношения:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

➤ Примечание. Чтобы понять доказательство, вам нужно знать, что такое производная гиперболического синуса и что такое производная гиперболического косинуса . Поэтому мы рекомендуем вам посетить связанные страницы, прежде чем продолжить.

Теперь применим формулу производной частного:

$\displaystyle\left(\text{tanh}(x)\right)'=\left(\frac{\text{senh}(x)}{\text{cosh}(x)}\right)'$

$\text{tanh}'(x)=\cfrac{\text{cosh}(x)\cdot \text{cosh}(x)-\text{senh}(x)\text{senh}(x) }{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

Сократим выражение числителя дроби по следующей формуле:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

$\text{tanh}'(x)=\cfrac{1}{\text{cosh}^2(x)}$

Как видите, предыдущее равенство соответствует первой формуле производной гиперболического тангенса. Аналогично, гиперболический секанс является мультипликативной обратной гиперболическому косинусу, поэтому выводится и вторая формула:

$\text{tanh}'(x)=\text{sech}^2(x)$