На этой странице вы найдете объяснение того, что означает линейная комбинация векторов. Кроме того, вы сможете увидеть пример того, как вектор выражается в виде линейной комбинации, и, кроме того, вы сможете попрактиковаться с упражнениями и задачами, решаемыми шаг за шагом.
Что такое линейная комбинация векторов?
Определение линейной комбинации следующее:
Линейная комбинация набора векторов — это вектор, полученный сложением всех векторов набора, умноженными на скаляры (действительные числа).
Другими словами, для данного набора векторов
![]()
их линейная комбинация будет:
![]()
Где коэффициенты
![]()
Это реальные цифры.
Следовательно, вектор, представляющий собой линейную комбинацию других векторов, означает, что первый можно выразить через второй.
Эту концепцию можно лучше понять, построив график вектора на плоскости, который представляет собой линейную комбинацию двух векторов:
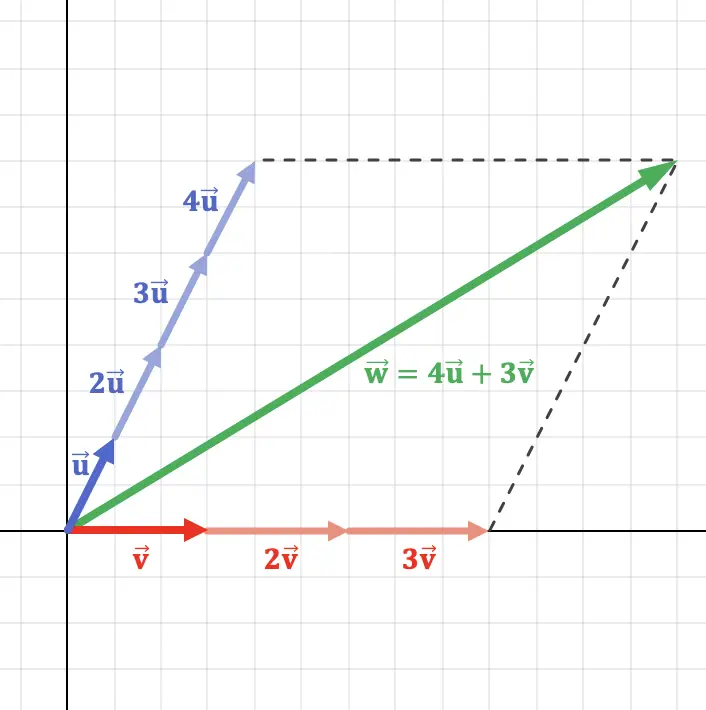
Как вы можете видеть на графическом представлении выше, вектор
![]()
можно получить из векторов
![]()
И
![]()
выполнять векторные операции. Следовательно, вектор
![]()
представляет собой линейную комбинацию двух других векторов.
Следует подчеркнуть, что эта линейная комбинация уникальна , или, другими словами, для каждого вектора существует только одна допустимая линейная комбинация. Поскольку, следуя предыдущему примеру, если мы умножили
![]()
для 6 вместо 4 мы получим другой вектор.
Кроме того, одно из свойств линейной комбинации на плоскости (в R2) состоит в том, что любой вектор можно представить как линейную комбинацию двух других векторов, если они имеют разные направления, т. е. если они не параллельны.
Кроме того, иногда мы можем на глаз определить, что два вектора представляют собой линейную комбинацию. Для этого достаточно, чтобы его компоненты были пропорциональны . Например, координаты следующих двух векторов пропорциональны и, следовательно, векторы представляют собой линейную комбинацию:
![]()
![Rendered by QuickLaTeX.com \cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac41542948764e158ebe590c6b36e67_l3.png)
Наконец, если в двумерном (в R2) или трехмерном (в R3) векторном пространстве существует линейная комбинация внутри набора векторов, это означает, что они линейно зависят друг от друга. С другой стороны, если между векторами невозможна линейная комбинация, это означает, что они линейно независимы .
Если последнее понятие вам не совсем понятно, рекомендуем ознакомиться с нашим объяснением линейно зависимых и независимых векторов , здесь вы найдете, что значит для векторов быть линейно зависимыми или независимыми, примеры каждого типа и различия между ними. . Это понятие часто используется и, на самом деле, его часто задают на экзаменах, поэтому важно, чтобы вы его хорошо поняли.
Как выразить вектор как линейную комбинацию других векторов
Затем мы увидим, как решить типичную задачу, в которой нас просят найти линейную комбинацию вектора.
- Выразите вектор
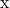
как линейная комбинация
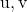
И
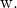
![]()
![]()
Так что вектор
![]()
быть линейной комбинацией других векторов, должно выполняться следующее уравнение:
![]()
Где коэффициенты
![]()
И
![]()
Это неизвестные, которые мы должны найти.
Поэтому мы заменяем каждый вектор его координатами:
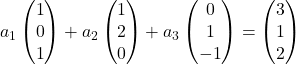
Умножаем каждый вектор на его коэффициент:
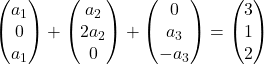
Добавляем векторы:
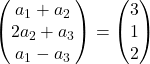
Каждая левая координата должна быть равна каждой правой координате. Таким образом, у нас есть 3 уравнения:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e5fe050102a285a325dcd81d07ef5d5_l3.png)
Остается только решить полученную систему уравнений. Для этого используйте предпочитаемый вами метод (метод замены, правило Крамера, метод Гаусса-Жордана и т. д.), в данном случае воспользуемся методом Гаусса:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8aa4e245614f286e0697797a18ba4465_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f1d9c941fe239bb40297b998eb6929_l3.png)
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-02a8a00406479f367627b682099e05c0_l3.png)
Таким образом, полученная система шагов такова:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-74ed1b18779582d6683ecaa1a9085e3d_l3.png)
Все, что нам нужно сделать сейчас, это прояснить неизвестное и найти его значение. Итак, из последнего уравнения находим
![]()
![]()
Из второго уравнения системы вычисляем значение
![]()
![]()
![]()
![]()
![]()
И, наконец, из первого уравнения системы шагов находим неизвестную
![]()
![]()
Таким образом, решение системы линейных уравнений имеет вид:
![]()
Итак, вектор
![]()
Его можно выразить следующей линейной комбинацией:
![]()
![]()
![]()
Таким образом, между векторами фактически существует линейная зависимость. С другой стороны, если бы решение системы уравнений не было получено, это означало бы, что вектор
![]()
Он линейно независим по отношению к другим векторам, и, следовательно, не существует возможной линейной комбинации для получения указанного вектора из других векторов.
Решенные упражнения на линейную комбинацию векторов
Упражнение 1
Среди следующих трех векторов укажите, какие пары являются линейными комбинациями друг друга. Кроме того, найдите отношение линейной комбинации указанных пар векторов.
![]()
Чтобы узнать, является ли пара векторов линейной комбинацией, мы должны проверить, пропорциональны ли их координаты.
Сначала проверяем вектор
![]()
с вектором
![]()
![]()
Во-вторых, мы проверяем вектор
![]()
с вектором
![]()
![]()
Наконец, мы проверяем вектор
![]()
с вектором
![]()
![Rendered by QuickLaTeX.com \cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f818eb5ae0825dd43290331519599c21_l3.png)
Таким образом, единственная пара векторов, представляющая собой линейную комбинацию, — это
![]()
И
![]()
Более того, их взаимоотношения таковы:
![]()
Или эквивалент:
![]()
Хотя утверждение этого не требует, единственными векторами, которые линейно зависят друг от друга, являются
![]()
И
![]()
потому что между ними существует линейная комбинация. Остальные пары линейно независимы, поскольку их нельзя объединить линейно.
Упражнение 2
Найдите линейную зависимость между вектором
![]()
и набор векторов
![]()
И
![]()
![]()
![]()
Так что вектор
![]()
быть линейной комбинацией других векторов, должно выполняться следующее уравнение:
![]()
Поэтому мы заменяем каждый вектор его координатами:
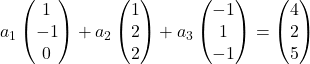
Умножим каждый вектор на его константу:
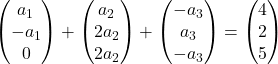
Добавляем векторы:
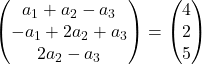
Таким образом, мы получаем следующую систему уравнений:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ea3ca998fc7d9d9b2cf42d43a5bf0a4_l3.png)
Решаем систему, полученную методом Гаусса:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c808441bc71bd26e333ebe2169b738ca_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-941792a2de155bc284b14e34dc561418_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7105de2fa579f40818bccc2df48961ab_l3.png)
Таким образом, полученная система шагов такова:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd5b2d564f66cd225c1a5987241ba14_l3.png)
Все, что нам нужно сделать сейчас, это прояснить неизвестное и найти его значение. Итак, из последнего уравнения находим
![]()
![]()
![]()
Из второго уравнения системы вычисляем значение
![]()
![]()
![]()
И, наконец, из первого уравнения системы шагов находим неизвестную
![]()
![]()
![]()
![]()
Таким образом, решение системы линейных уравнений имеет вид:
![]()
Итак, вектор
![]()
Его можно выразить следующей линейной комбинацией:
![]()
![]()
![]()
Упражнение 3
Выразите вектор
![]()
как линейная комбинация векторов
![]()
И
![]()
![]()
![]()
Мы предлагаем линейное комбинационное уравнение относительно вектора
![]()
![]()
Поэтому мы заменяем каждый вектор его компонентами:
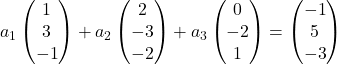
Мы умножаем каждый вектор на соответствующее ему неизвестное:
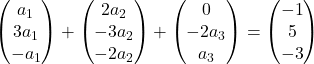
Осуществляем сложение векторов:
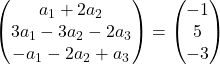
Таким образом, мы получили следующую систему уравнений:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-acdcf13a945bca16684be340d27e3523_l3.png)
Решаем систему, полученную методом Гаусса:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e49ae26fc68a865214bd9b6146b7aa99_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4c56b420242d0abe6f77b3ed1a60e54_l3.png)
Таким образом, полученная система шагов такова:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-03461ed9ebda463d2f0a1bb6894657be_l3.png)
Все, что нам нужно сделать сейчас, это прояснить неизвестное и найти его значение. Итак, из последнего уравнения находим
![]()
![]()
Из второго уравнения системы находим значение
![]()
![]()
![]()
![]()
![]()
![]()
И наконец, из первого уравнения системы шагов решаем неизвестное
![]()
![]()
Таким образом, решение системы линейных уравнений имеет вид:
![]()
Итак, вектор
![]()
может быть выражено путем линейного объединения других векторов:
![]()
![]()
![]()
Упражнение 4
Определите, является ли вектор
![]()
можно выразить как линейную комбинацию векторов
![]()
И
![]()
В этом случае найдите выражение, которое их связывает.
![]()
![]()
Так что вектор
![]()
быть линейной комбинацией других векторов, должно выполняться следующее уравнение:
![]()
Поэтому мы заменяем каждый вектор его координатами:
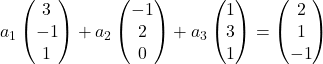
Умножаем каждый вектор на его коэффициент:
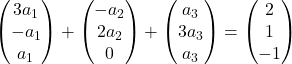
Добавляем векторы:
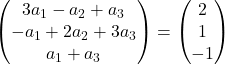
Таким образом, предыдущее выражение эквивалентно следующей системе уравнений:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f51b7e801b8314c51b983f1f24be15e4_l3.png)
Решим теперь систему, полученную методом Гаусса:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-031b14d5aca6a41d897ca575440b1197_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2caf1e1104b8b67e13d452bbd20d13b0_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4deec2426c0b9bb0b8e8a3d95155fd9_l3.png)
Таким образом, мы получили следующую систему уравнений:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e537d5c481ceedeaebf95334d72199ad_l3.png)
Однако последнее уравнение никогда не может быть выполнено, поскольку 0 никогда не будет равен -30, какие бы значения ни принимали неизвестные. Следовательно, система не имеет решения, а это означает, что не существует линейной комбинации для вычисления вектора
![]()