На этой странице вы узнаете, что такое копланарные (или копланарные) точки и как узнать, являются ли определенные точки компланарными или нет. Кроме того, вы сможете увидеть примеры и попрактиковаться с решенными упражнениями по копланарным точкам.
Что такое компланарные точки?
В аналитической геометрии значение компланарных (или компланарных) точек следующее:
Компланарные точки — это точки, принадлежащие одной плоскости.
Следовательно, 2 или 3 точки всегда компланарны, поскольку плоскость можно сформировать всего из 3 точек. С другой стороны, при наличии 4, 5 и более точек возможно, что некоторые из них не содержатся в одной плоскости и, следовательно, некомпланарны.
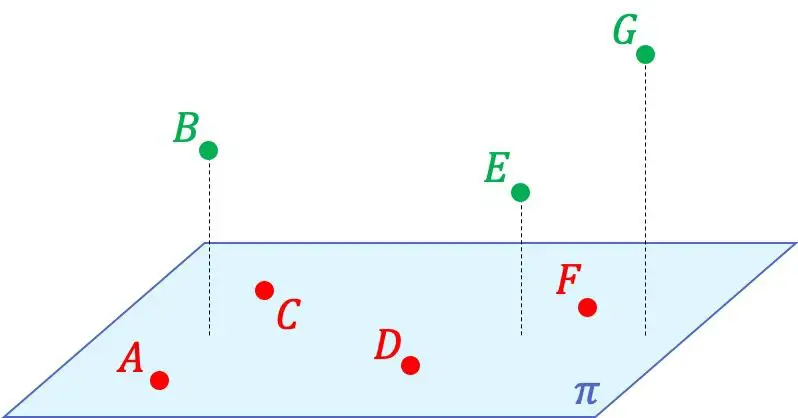
Например, на графическом представлении выше вы можете видеть, что точки A, C, D и F компланарны друг другу, поскольку содержатся в одной плоскости. С другой стороны, эти четыре точки не компланарны точкам B, E и G, поскольку в пространстве, содержащем все точки, не может быть образована плоскость.
Из этого свойства мы можем сделать вывод, что векторы, определяемые компланарными точками, также являются компланарными векторами, то есть содержатся в одной плоскости.
Когда точки компланарны?
Как мы видели в определении копланарных (или копланарных) точек, две или три точки всегда компланарны, но более трех точек не обязаны соблюдать соотношение компланарности.
Итак, существует в основном 2 метода определения того, являются ли четыре или более точек компланарными:
- Один из способов узнать, являются ли точки копланарными, — это использовать векторы, которые определяются точками: если эти векторы компланарны , то точки также компланарны.
Очевидно, что для применения этого метода необходимо знать, когда векторы компланарны. Но поскольку существует также несколько способов определить, является ли набор векторов компланарным, мы рекомендуем проверить , как определить, являются ли векторы компланарными . Здесь вы найдете все существующие процедуры для определения того, когда 2, 3, 4 или более векторов компланарны, а также примеры и решенные упражнения.
- Другой способ узнать, является ли набор точек компланарным, — найти уравнение плоскости, образованной тремя точками набора, и если остальные точки удовлетворяют этому уравнению, то это означает, что все точки набора компланарны.
Хотя это зависит от задачи, мы рекомендуем использовать первый из двух способов, поскольку проверить компланарность векторов гораздо проще и быстрее, чем вычислять уравнение плоскости. Но, очевидно, используйте тот, который вам больше нравится.
Решенные задачи о копланарных точках
Упражнение 1
Определите, являются ли следующие три точки компланарными:
![]()
![]()
![]()
В этом случае нет необходимости делать какие-либо расчеты, поскольку 3 точки всегда лежат в одной плоскости , какими бы они ни были.
Упражнение 2
Определите, являются ли следующие четыре точки компланарными:
![]()
![]()
![]()
![]()
Чтобы четыре точки были компланарными, определяемые ими векторы должны быть компланарными. Поэтому мы вычисляем эти векторы:
![]()
![]()
![]()
Построим теперь матрицу, образованную векторами:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-873ec750665fdf215a648778d6fcf042_l3.png)
Чтобы полученные векторы были компланарными, ранг предыдущей матрицы должен быть равен 2. А для этого определитель всей матрицы 3х3 должен быть равен нулю:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-3eadb62f19c07b8a646fe9b2a00f9003_l3.png)
![]()
Однако определитель всей матрицы ненулевой, поэтому ранг матрицы равен 3, а значит , 4 точки не компланарны .
Упражнение 3
Выясните, являются ли следующие пять точек компланарными:
![]()
![]()
![]()
![]()
![]()
Чтобы все пять точек были копланарными, определяемые ими векторы должны быть компланарными. Поэтому мы вычисляем эти векторы:
![]()
![]()
![]()
![]()
Давайте теперь построим матрицу, состоящую из векторов:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d571ea172dbf5e6b7d85da6db466eb0_l3.png)
Чтобы полученные векторы были копланарными, ранг предыдущей матрицы должен быть равен 2. Поэтому мы вычисляем ранг матрицы векторов по определителям, чтобы проверить, являются ли они компланарными:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bec15883d9e3aa5a401afa41cd3992ae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-cd2f8cfa577e91b74c69e50cc36dfd9a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3&-1 \\[1.1ex] 1&-3\end{vmatrix} =10\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d551dddceb916cc6cf8bf4137903da1d_l3.png)
![]()
Ранг матрицы эквивалентен 2, поэтому векторы компланарны и, следовательно , 5 точек также компланарны.
Упражнение 4
Рассчитать значение параметра
![]()
так что следующие 4 точки лежат в одной плоскости:
![]()
![]()
![]()
![]()
Чтобы четыре точки были компланарными, определяемые ими векторы должны быть компланарными. Поэтому мы вычисляем эти векторы:
![]()
![]()
![]()
Чья векторная матрица:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3d801efcf5b56dd858890720797d6a4_l3.png)
Чтобы результирующие векторы были компланарными, ранг матрицы должен быть равен 2. И, следовательно, определитель всей матрицы 3х3 должен быть равен 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bb7d3b31c10096d100843d781a85b621_l3.png)
![]()
Наконец, мы решаем неизвестное
![]()
![]()
![]()
Наконец, если эта статья была вам полезна, вас наверняка также интересует, как рассчитывается расстояние между двумя точками (формула) , поскольку иногда в задачах аналитической геометрии нас спрашивают, каково расстояние между двумя точками. На связанной странице вы найдете очень подробное объяснение, а также примеры и упражнения, решаемые шаг за шагом.