Симметричная матрица

На этой странице вы найдете объяснение того, что такое симметричные матрицы. Кроме того, мы покажем вам, как быстро определить, является ли матрица симметричной, а также приведем несколько примеров, чтобы у вас не осталось сомнений. Вы также найдете все свойства симметричных матриц. И, наконец, мы объясним особенность, которой обладает любая квадратная матрица: ее можно разложить на сумму симметричной и антисимметричной матриц.

Что такое симметричная матрица?

Определение симметричной матрицы следующее:

Симметричная матрица — это квадратная матрица, транспонирование которой равно самой матрице.

$A^t = A$

Золото

$A^t$

представляет собой транспонированную матрицу

$A$

Как только мы узнаем понятие симметричной матрицы, мы увидим, как можно легко идентифицировать любую симметричную матрицу:

Когда матрица является симметричной?

Распознать структуру симметричной матрицы очень просто: элемент строки i и столбца j должен быть идентичен элементу строки j и столбца i . А значения главной диагонали матрицы могут быть любыми.

Примеры симметричных матриц

Вот несколько примеров симметричных матриц, которые помогут вам понять:

Пример симметричной матрицы порядка 2 × 2

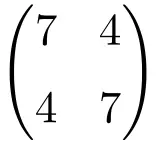
пример симметричной матрицы размерности 2х2

Пример симметричной матрицы размерности 3×3

пример симметричной матрицы размерностью 3х3

Пример симметричной матрицы размером 4х4

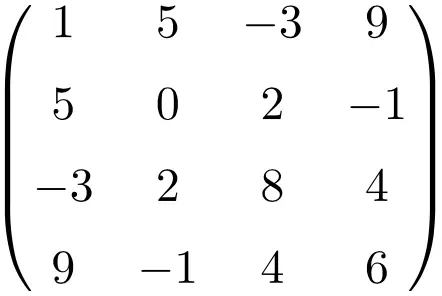
пример симметричной матрицы размерностью 4х4

Транспонируя эти три матрицы, мы проверяем, что они симметричны, поскольку транспонированные матрицы эквивалентны соответствующим исходным матрицам.

Почему ее называют симметричной матрицей?

Если внимательно присмотреться к предыдущим примерам, то главная диагональ симметричной матрицы является осью симметрии, или другими словами, она действует как зеркало между числами выше диагонали и числами ниже. По этой причине такие типы матриц называются симметричными.

Свойства симметричных матриц

Характеристики симметричных матриц следующие:

Сложение (или вычитание) двух симметричных матриц дает еще одну симметричную матрицу. Поскольку транспонирование двух добавленных (или вычтенных) матриц эквивалентно транспонированию каждой матрицы отдельно:

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

Любая симметричная матрица, умноженная на скаляр, также порождает другую симметричную матрицу.

Аналогично, матричное произведение двух симметричных матриц не всегда равно другой симметричной матрице, только тогда и только тогда, когда две матрицы можно коммутировать. Это условие можно доказать с помощью свойства умножения транспонированной матрицы:

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

Степень симметричной матрицы порождает другую симметричную матрицу, если показатель степени является целым числом.

Очевидно, что унитарная матрица и нулевая матрица являются примерами симметричных матриц.

Матрица, конгруэнтная симметричной матрице, также должна быть симметричной.

Если симметричная матрица является регулярной или обратимой, то и ее обратная матрица также является симметричной.

То же самое и с сопряженной симметричной матрицей: присоединенная матрица симметричной матрицы дает в качестве решения другую симметричную матрицу.

Настоящая симметричная матрица также является нормальной матрицей.

Поскольку симметричные матрицы являются частным случаем эрмитовых матриц, все собственные значения (или собственные значения) симметричной матрицы являются действительными числами.

Спектральная теорема говорит нам, что все матрицы, элементы которых вещественны, являются диагонализуемыми матрицами, причем диагонализация осуществляется с помощью ортогональной матрицы. Следовательно, все вещественные симметричные матрицы ортогонально диагонализуются.

С другой стороны, симметричные матрицы с комплексными числами можно диагонализовать с помощью унитарной матрицы.

Матрица Гессе всегда симметрична.

Разложение квадратной матрицы на симметричную и антисимметричную матрицу

Особенностью квадратных матриц является то, что их можно разложить на сумму симметричной матрицы и антисимметричной матрицы.

Формула, которая позволяет нам это сделать, выглядит следующим образом:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Где C — квадратная матрица, которую мы хотим разложить, C ^— ее транспонировать, и, наконец, S и A — соответственно симметричная и антисимметричная матрицы, на которые разлагается матрица C.

Ниже вы найдете решенное упражнение, чтобы увидеть, как это делается. Разложим следующую матрицу:

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

Рассчитаем симметричную и антисимметричную матрицу по формулам:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

И мы можем проверить, что уравнение выполняется, сложив две матрицы:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$

✅