На этой странице мы объясняем, как применять правило Руффини для деления многочленов. Помимо пояснений, вы сможете увидеть примеры и пошагово решаемые упражнения на деление многочленов по правилу Руффини. Кроме того, вы найдете все применения этого метода и, на самом деле, не одно вас наверняка удивит.
В чем заключается правило Руффини?
В математике правило Руффини — это алгебраический метод, позволяющий быстро разделить любой многочлен на многочлены вида xr . Правило Руффини названо в честь математика Паоло Руффини, который изобрел этот метод.
Однако правило Руффини используется не только для деления многочленов, оно имеет множество других применений. Например, правило Руффини также используется для поиска корней многочлена, для нахождения числового значения многочлена, для факторизации многочлена или даже для решения уравнений третьей степени или выше. Ниже мы увидим, как применяется правило Руффини, чтобы иметь возможность выполнять все эти операции.
Наконец, правило Руффини также известно как метод Руффини, теорема Руффини или синтетическое деление многочленов.
Как применять правило Руффини
Как мы видели, основное применение правила Руффини состоит в том, чтобы разделить многочлен на бином, то есть произвести деление следующего типа:
![]()
Обратите внимание, что для использования правила Руффини делящий полином всегда должен быть образован х (с коэффициентом, равным 1) и числом (положительным или отрицательным), в противном случае алгоритм Руффини использовать нельзя.
Чтобы применить правило Руффини, необходимо выполнить целую процедуру, поэтому ниже мы шаг за шагом решим пример, чтобы увидеть, как применяется правило Руффини (или метод Руффини).
Пример правила Руффини
- Решите следующее деление многочленов, используя правило Руффини:
![]()
Прежде всего вам нужно нарисовать две перпендикулярные линии, пересекающие друг друга, затем расположить делимое и делитель следующим образом:
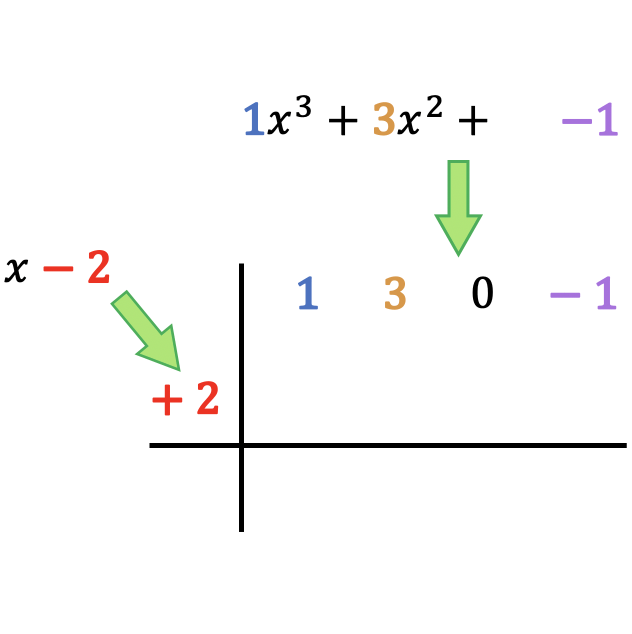
Как видите, мы должны положить вверху коэффициенты делимого полинома, упорядоченные от высшей степени к низшей, а независимый член делителя полинома поместить слева от поля со сменой знака .
Внимание: если в делимом полиноме нет члена определенной степени (неполный полином), на его месте ставится 0. Например, в этом случае полином
![]()
Одночлена степени 1 у него нет, поэтому вместо него ставим 0.
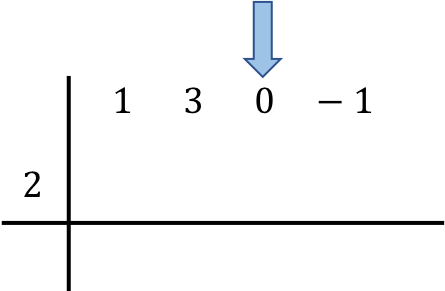
После того, как мы расположили полиномы, участвующие в операции, мы опускаем первое число непосредственно в строку ниже:
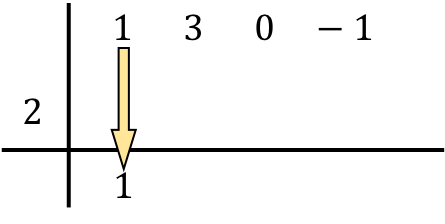
Теперь наступает шаг, характеризующий правило Руффини: мы умножаем число ниже на число слева и помещаем результат в следующий столбец :
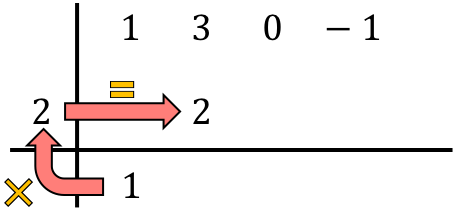
И складываем цифры в столбик, помещая результат суммы чуть ниже:
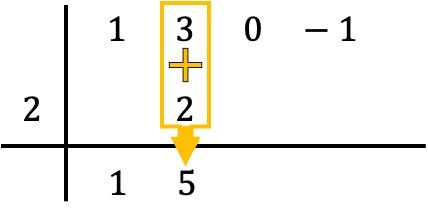
Итак, метод Руффини предполагает повторение этого процесса. Итак, мы делаем то же самое еще раз: умножаем нижнее число на число слева, помещаем результат в следующий столбец и, наконец, складываем числа, выровненные по вертикали:
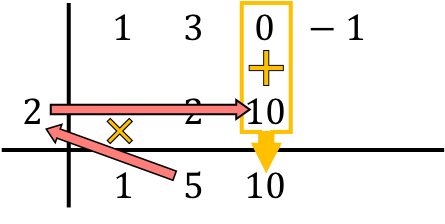
И повторяем ту же процедуру последовательно до конца. Сначала делаем произведение числа ниже на число слева, затем помещаем результат в следующий столбец и, наконец, складываем числа в том же столбце:
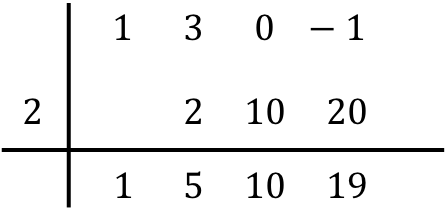
Итак, когда мы заполнили все столбцы, это означает, что мы закончили деление многочленов.
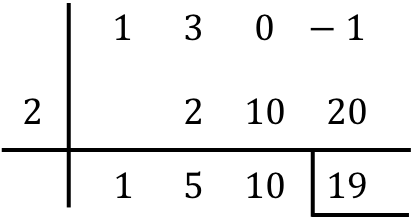
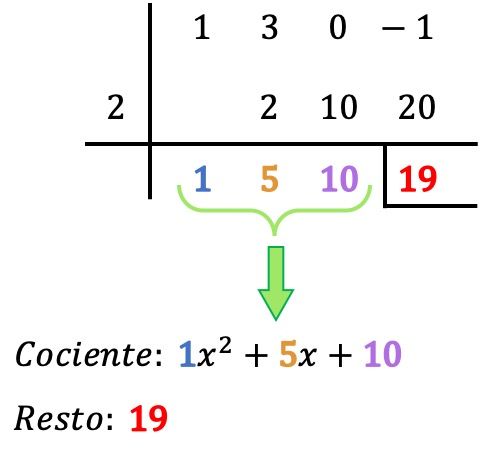
Значит вам просто нужно найти результат деления многочленов:
- Остаток деления между двумя полиномами представляет собой последнее число в строке ниже, поэтому в нашем случае остаток равен 19. Остаток обычно обозначается путем размещения полосы слева и другой под указанным числом.
- Частное деления многочлена определяется по другим полученным значениям, которые являются коэффициентами частного многочлена. Первая цифра справа соответствует коэффициенту семестра 0 класса, следующая цифра — коэффициент семестра 1 класса, следующая — 2 класса, следующая — 3 класса… и так до конца. . ТАК:
Решенные упражнения правила Руффини.
Ниже вы найдете несколько решенных пошаговых упражнений по правилу Руффини, чтобы вы могли попрактиковаться и понять, как решать деление многочленов с помощью этого метода. Мы рекомендуем вам попробовать каждое упражнение, а затем проверить, правильно ли вы его выполнили, посмотрев на исправление.
Упражнение 1
Выполните следующее деление полиномов по правилу Руффини:
![]()
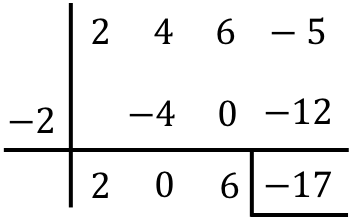
Таким образом, результатом деления двух полиномов будет:
Коэффициент:
![]()
Отдых:
![]()
Упражнение 2
Рассчитайте следующее деление многочленов, используя правило Руффини:
![]()
В этом конкретном случае дивидендный полином не имеет члена второй степени, поэтому мы должны поставить вместо него ноль:
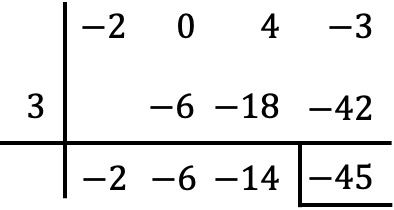
Таким образом, результатом деления двух полиномов будет:
Коэффициент:
![]()
Отдых:
![]()
Упражнение 3
Найдите результат следующего деления многочленов по правилу Руффини:
![]()
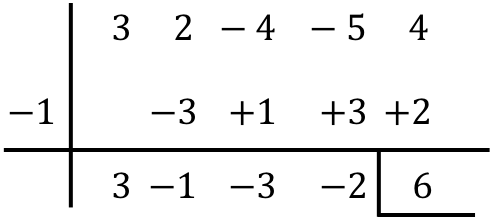
В заключение, результатом деления двух многочленов является:
Коэффициент:
![]()
Отдых:
![]()
Упражнение 4
Найдите значение неизвестного m так, чтобы остаток от следующего деления многочленов был эквивалентен 5:
![]()
Поскольку делитель имеет форму (xr) или (x+r), мы можем применить правило Руффини для решения деления. Поэтому мы применяем метод Руффини, перетаскивая неизвестное m:
Теперь приравниваем полученный остаток к 5, потому что остаток должен быть 5:
![]()
И решаем уравнение, чтобы найти значение параметра m :
![]()
![]()
Итак, когда переменная m эквивалентна 3, остаток от деления между многочленами будет равен 5.
Упражнение 5
Определите значение параметра m так, чтобы остаток от следующего полиномиального деления давал 3:
![]()
Поскольку делитель имеет форму (xr) или (x+r), мы можем применить правило Руффини для решения деления. Поэтому воспользуемся методом Руффини, перетащив неизвестное m:
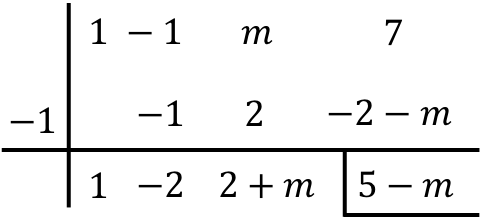
Учитывайте распределительное свойство при последнем умножении:
![]()
С другой стороны, расчет остатка от деления таков:
![]()
![]()
![]()
Теперь приравняем полученное выражение остатка к 3, так как остаток от деления должен быть равен 3:
![]()
И решаем полученное уравнение, чтобы определить значение параметра m :
![]()
![]()
![]()
![]()
Следовательно, m должно равняться 2, чтобы остаток от деления полинома был равен 3.
Другие применения правила Руффини
Как уже объяснялось, правило Руффини в основном используется для деления полиномов. Однако правило Руффини используется и для выполнения других расчетов, каждый из них мы увидим ниже.
Корни многочлена
Корни многочлена легко найти с помощью правила Руффини. Если вы не знаете, что такое корень многочлена, давайте рассмотрим его определение:
Корни (или нули) многочлена — это значения, сокращающие многочлен. Или другими словами, корни многочлена — это все те значения, которые при вычислении в многочлене имеют числовое значение, равное 0.
![]()
С другой стороны, благодаря теореме об остатках мы знаем, что если числовое значение многочлена для данного значения
![]()
равно нулю, обязательно остаток от деления указанного многочлена между
![]()
Оно также должно быть 0.
![]()
Следовательно, если вы используете правило Руффини для деления многочлена
![]()
между другим многочленом вида
![]()
получим остаток, равный 0, это означает, что
![]()
является корнем многочлена
![]()
На примере мы наверняка лучше поймем:
- Проверить, если
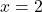
является корнем многочлена
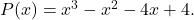
Чтобы проверить, является ли данное значение корнем полинома, просто примените метод Руффини с указанным полиномом и указанным значением:
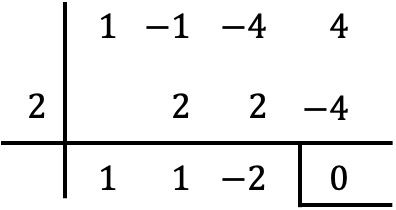
Поскольку остаток, полученный по правилу Руффини, равен нулю, это означает, что эффективно
![]()
является корнем многочлена
![]()
Факторинг полиномов
Правило Руффини — это метод, обычно применяемый к факториальным многочленам, поскольку он позволяет быстро узнать все корни многочлена степени 3, 4, 5 и т. д.
Итак, давайте посмотрим, как факторизовать полином с помощью алгоритма Руффини, на примере:
- Распределите следующий полином третьей степени:
![]()
Первое, что нужно сделать, это найти все корни многочлена. А возможные корни многочлена — это делители независимого члена, который в данном случае равен 6. Итак:
Возможные корни многочлена: +1, -1, +2, -2, +3, -3, +6, -6.
Теперь нам нужно попытаться разделить полином между каждым из этих значений с помощью правила Руффини. Если остаток от деления равен 0, это означает, что значение является корнем многочлена; однако, если остаток от деления не равен 0, значение не является корнем многочлена. Таким образом, проверка правила Руффини со всеми числами отменяет остаток только в следующих трех случаях:
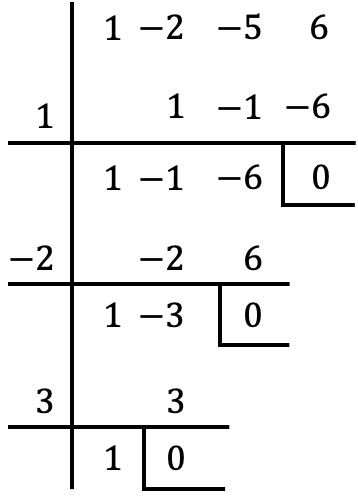
Следовательно, корнями многочлена в задаче являются значения, при которых остаток обращается в нуль, то есть:
![]()
Наконец, чтобы факторизовать многочлен, мы должны выразить каждый корень
![]()
в виде фактора вида
![]()
, то есть для каждого корня необходимо поставить скобку с
![]()
и найденный корень поменял знак:
![]()
Как видите, мы успешно факторизовали полином, используя правило Руффини. Однако у вас могли возникнуть сомнения по поводу факторизации полиномов, поскольку это очень сложная тема. В этом случае вы можете найти на нашем веб-сайте (в поисковой системе вверху справа) нашу статью о том, как факторизовать многочлены , там мы объясняем это более подробно, и вы можете попрактиковаться с ней в упражнениях, решаемых шаг за шагом. Кроме того, мы также покажем вам другие методы факторизации полиномов.
Вычислить числовое значение многочлена
Хотя это может показаться удивительным, числовое значение многочлена можно определить по правилу Руффини с использованием теоремы об остатках.
Но очевидно, что для этого нужно знать теорему об остатках. Если это не так, то объяснение теоремы об остатках можно поискать на нашем сайте (в поисковике справа вверху) .
Итак, благодаря теореме об остатках мы можем узнать числовое значение любого многочлена. Давайте посмотрим, как это сделать на примере:
- Вычислите числовое значение

Для
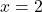
применяя правило Руффини, будучи
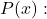
![]()
Чтобы найти числовое значение многочлена для значения
![]()
Единственное, что нам нужно сделать, это использовать правило Руффини с полиномом и указанным значением:
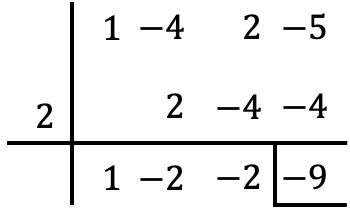
Итак, из теоремы об остатках мы знаем, что числовое значение многочлена совпадает с остатком от деления многочлена . Следовательно, численное значение многочлена в
![]()
это -9.
![]()
С другой стороны, мы можем проверить правильность применения правила Руффини, численно рассчитав числовое значение:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
Решайте уравнения третьей степени и выше.
Другое применение правила Руффини — решение уравнений степени больше 2, поскольку в этих случаях нет формулы, как в уравнении второй степени. Давайте посмотрим, как это сделать на примере:
- Решите следующее квадратное уравнение, используя правило Руффини:
![]()
Нам нужно относиться к уравнению так, как если бы оно было полиномом. Затем мы должны вычислить столько корней «многочлена», используя правило Руффини, пока не получим уравнение второй степени . В данном случае это уравнение степени 3, поэтому достаточно определить корень «многочлена»:
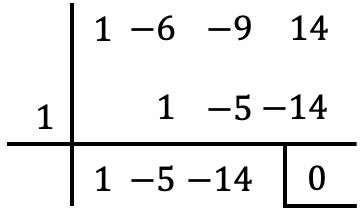
Таким образом, решение уравнения будет
![]()
Ну а чтобы найти остальные решения, надо полученный полином в частном по правилу Руффини положить равным 0:
![]()
А теперь решаем полученное квадратное уравнение по соответствующей ему формуле:
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
В заключение, три решения уравнения третьей степени:
![]()