Полиномиальный

Моном – это алгебраическое выражение , образованное коэффициентом (числовым значением), который умножает переменную на показатель степени, например, выражение 4x² является мономом. Итак, из этой математической концепции мы приходим к многочлену, который представляет собой набор сложений и вычитаний нескольких мономов. На изображении выше вы можете увидеть пример структуры многочлена, составленного из нескольких мономов.

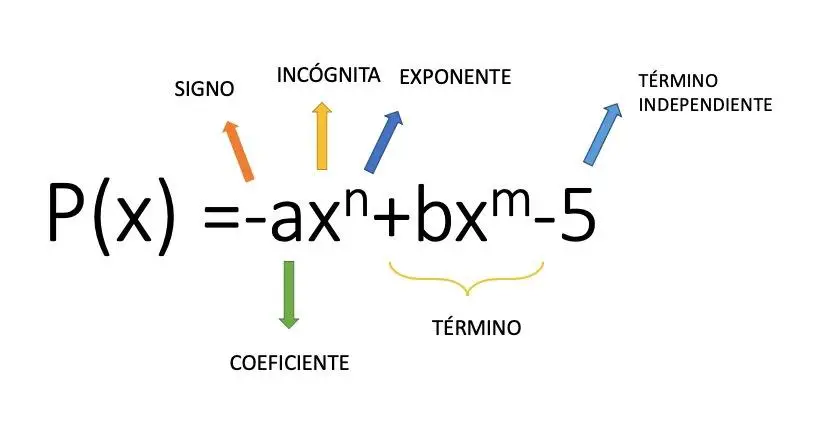
типы полиномов

По показателю степени определенного монома мы можем классифицировать многочлены на разные типы. Мы можем классифицировать эти выражения по таким категориям, как: полином первой степени, полином второй степени, полином третьей степени и т. д. По сути, вам нужно определить моном, который имеет наибольший показатель и который будет степенью многочлена . И как только вы это узнаете, вы сможете отнести его к одному из типов, о которых мы только что говорили.

Полином нескольких переменных

Кроме того, существует еще один способ организации многочленов — по количеству образующих их мономов. Например, если у нас есть бином , это будет эквивалентно наличию многочлена с двумя членами, если у нас есть трехчлен , это будет эквивалентно наличию многочлена с тремя членами и т. д. Все эти способы каталогизации полиномов имеют бесконечное количество подкатегорий. Поскольку эти выражения могут состоять из любых одночленов, а также иметь любую степень.

Характеристики и свойства многочленов

• Абсолютная степень многочлена. В предыдущем разделе мы обсудили определение относительной степени. Но в случае многочленов, образованных более чем одной переменной, мы имеем абсолютную степень, которая эквивалентна максимальной сумме показателей всех переменных этого монома. Например, в мономе 5x²y³ абсолютная степень равна 2 + 3 = 5.
• Упорядоченный полином: мы определяем упорядоченный полином по отношению к переменной, когда показатели этой переменной расположены в порядке возрастания или убывания. Например, если мы найдем этот многочлен P(x) = 3x + 4x³ – x², в этом случае он не будет упорядочен. Значит, нам следует это исправить, и мы получим такой результат: P(x) = 4x³ – x² + 3x.
• Полный полином: когда мы находим многочлен, который имеет мономы со всеми возможными показателями (от высшей степени до независимого члена), мы говорим, что это полный многочлен . Например, следующее выражение: P(x) = 3 x² + 2x – 4 относится к этому типу, поскольку между 2 и 0 нет пропущенного показателя степени.
• Однородный многочлен: это многочлен, который имеет одинаковую абсолютную степень в каждом из своих мономов. Переменные могут иметь разные значения в показателе степени, но сумма показателей переменных во всех мономах обязательно должна быть одинаковой. Например: P(x) = x²y³z + 3 x ⁴ yz, две суммы дают шесть: 2 + 3 + 1 = 4 + 1 + 1 = 6.
• Идентичные полиномы: когда мы находим два или более полиномов, которые имеют одинаковые коэффициенты, мы говорим, что они являются идентичными полиномами. Ниже вы можете увидеть пример двух полиномов: P(x) = 2x + 27 и Q(x) = 5 (x + 3) – 3 (x – 4), они будут идентичными, поскольку имеют общие коэффициенты каждого показателя степени. : 2х = 5х – 3х и 27 = 15 + 12.
• Нулевой полином: этот полином имеет только нулевые коэффициенты (равные нулю), поэтому общее значение полинома также будет равно нулю. Полином P(x) = 0x³ + 0x² – 0x – 0 является наглядным примером полинома этого типа, но его не следует путать с Q(x) = 0, поскольку в этом случае вы составляете уравнение, а оно не не означает, что все коэффициенты Q(x) равны 0.

Числовое значение полинома

Числовое значение многочлена — это результат, который мы получим, заменив число переменной этого выражения. Нам просто нужно решить этот полином, как если бы это была комбинированная операция . Далее мы объясним три метода, которые можно использовать для получения числового значения такого выражения.

• Прямая замена: когда нам непосредственно задаются значения, соответствующие каждой из переменных многочлена, мы просто подставляем эти числа этими переменными. Таким образом, если у нас есть многочлен P(x) = 2x² – x + 4 и нам говорят, что x = 3, то числовое значение многочлена будет равно 2 · 3² – 3 + 4 = 19.
• Разрешение переменных: мы будем применять этот случай, когда они не дают нам напрямую значение переменной, но дают нам эквивалентность. Например, P(2), если P(x – 1) = x³ – 2x + 1 верно, то мы сначала решим уравнение 2 = x – 1 и получим x = 3. Наконец, нам придется заменить 3 на x, такой, что 3³ – 2 · 3 + 1 = 22.
• Замена переменной: когда у нас есть полином P(x) = 4x – 2 и мы хотим узнать это значение для P(x + 2). Далее нам нужно заменить все x в выражении на a(x+2). Тем не менее, давайте посмотрим, как будет выглядеть этот последний решенный пример: P (x + 2) = 4 (x + 2) – 2.

Операции с полиномами

Ниже мы объясним, как решать четыре основные арифметические операции с многочленами , всегда следуя иерархии операций . В каждом разделе вы найдете немного теории, которая позволит вам знать, как действовать в каждом конкретном случае, а также несколько практических примеров.

сложение полиномов

Чтобы добавить многочлены, мы должны принять во внимание тот факт, что их можно сгруппировать только по схожим терминам , поэтому, если у нас есть многочлены P(x) = 3x³ – x² + 2x – 4 и Q(x) = 2x² + 3x – 2. Итак, чтобы получить P(x) + Q(x), мы сложим коэффициенты двух многочленов, сопровождаемых одним и тем же показателем: P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. Подводя итог, можно сказать, что мы сгруппировали и сложили коэффициенты каждого подобного слагаемого и в итоге выразили все слагаемые в один полином. .

вычитание полиномов

Вычитание многочленов решается так же, как и сложение, единственное отличие, очевидно, состоит в символе. Затем мы группируем похожие термины вместе, вычитаем и преобразуем все это в одно выражение. Ниже мы покажем вам на примере: P(x) = 5x³ – 2x² + x – 3 и Q(x) = 3x² + 5x + 4, тогда P(x) – Q(x ) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1.

полиномиальное умножение

При решении этого типа умножения все может немного усложниться, но если вы выполните все шаги, о которых мы вам расскажем, то все будет в порядке. В этой математической операции все одномы будут оперировать всеми остальными, а это значит, что мы не будем только умножать подобные члены. Кроме того, изменятся не только коэффициенты , но и показатели степени . На этом примере вы все поймете гораздо лучше: P(x) = 2x² + 3x – 1 и Q(x) = 2x + 3:

P(x) Q(x) = ( 2x² + 3x –1 ) · ( 2x + 3 «=» 2x² · 2x + 2x² · 3 + 3x · 2x + 3x · 3 + (-1 ) · 2x + (-1 ) · 3 = 4x³ + 6x² + 6x² + 9x – 2x – 3 = 4x³ + 12x² + 7x – 3

По сути, мы умножаем коэффициенты каждого члена многочлена на все коэффициенты второго, а затем применяем степенное свойство a ⁿ · a ^m = a ^n+m .

деление многочленов

Наконец, нам нужно только объяснить, как решать деление многочленов, в основном нам нужно применить распределительное свойство деления: (a + b + c) ÷ d = (a ÷ d) + (b ÷ d) + (c ÷ г). И мы также применим следующее свойство возведения в степень к ⁿ ÷ a ^m = a ^nm . Теперь мы увидим это на простом примере: P(x) = 3x³ – 6x² + 9x и Q(x) = 3x.

P(x) ÷ Q(x) = ( 3x³ – 6x² +9x ) ÷ 3x «=» 3x³ ÷ 3x ) + ( 6x² ÷ 3x ) + (9x ÷ 3x ) = х² – 2х + 3

Теперь, когда вы узнали, как решать все эти операции с полиномами, мы надеемся, что вы знаете, как применить это на практике. Но если вы считаете, что это не так и хотите немного продолжить занятия, то рекомендуем вам посмотреть некоторые решенные упражнения на этой странице . Это поможет вам завершить усвоение всех этих математических концепций.

Факторинг полиномов

Чтобы факторизовать полиномы, вы можете сделать это вручную, как описано в статье по последней ссылке, или вы можете сделать это с помощью калькулятора Руффини . Мы рекомендуем делать это с помощью второго варианта, если вы хотите сделать это быстро, но если вы только учитесь факторингу, то вам лучше потренироваться вручную. Способ сделать это следует выбирать исходя из вашей ситуации.

Решайте полиномы с помощью научного калькулятора

Сегодня на рынке представлено множество различных научных калькуляторов. Но если вы ищете дешевый калькулятор , способный решать полиномы , мы рекомендуем Casio FX-991SPX II . Он прост в использовании, очень мощный и функциональный, что делает его идеальным для любого ученика средней и старшей школы. Ниже мы кратко объясним, как математические выражения этого стиля решаются с использованием этой или аналогичной модели Casio.

Сначала необходимо ввести числовое значение переменных, написать его, затем нажать «STO» + букву переменной , например x. Итак, когда все переменные определены, вам просто нужно написать полиномиальное выражение как есть со всеми переменными и всеми числами. И, наконец, необходимо нажать клавишу равенства, таким образом вы получите результат, эквивалентный числовому значению многочлена.