На этой странице вы найдете объяснение того, что такое плоскость, как она рассчитывается и все ее свойства. Кроме того, вы сможете увидеть примеры плоскостей, каковы относительные положения между двумя плоскостями, как определить угол между двумя плоскостями и, наконец, как выразить любую плоскость численно с помощью уравнений плоскости.
Что такое план?
В аналитической геометрии определение плоскости следующее:
Плоскость – это геометрический объект, имеющий два измерения (длину и ширину).
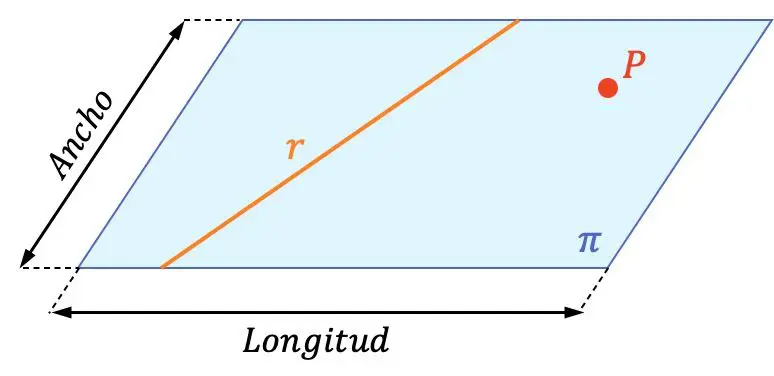
Следовательно, плоскость содержит бесконечные линии и бесконечные точки. В графическом представлении выше вы можете увидеть разницу между плоскостью, линией и точкой. Вы также можете убедиться, что строка
![]()
и кончик
![]()
содержатся в плоскости
![]()
Как вы можете видеть на графическом плане, планы обычно называются греческими буквами:
![]()
Примером плоскости, которую мы часто используем в математике, является декартова плоскость. Декартова плоскость — это плоскость, определяемая осью абсцисс (ось X) и осью ординат (ось Y). Одно из применений декартовой плоскости заключается в том, что она используется для описания положения объекта в системе отсчета.
Определение плана
Теперь, когда мы поняли значение плоскости, давайте посмотрим, как можно определить любую плоскость в трехмерном пространстве (в R3).
План полностью определяется следующими геометрическими элементами:
- Три точки не совпадают.
- Прямая линия и точка снаружи.
- Две параллельные прямые или две пересекающиеся линии.
Что касается последнего пункта, вы, вероятно, уже знаете, что значит, что две прямые параллельны. Но значение секущих линий менее известно, поэтому, если у вас есть вопросы, вы можете узнать , что такое секущие линии .
Следовательно, если у нас есть какое-либо из предыдущих 3-х условий, значит, мы можем сформировать план.
свойства плана
План соответствует следующим характеристикам:
- Плоскость содержит бесконечное количество точек.
- Плоскость содержит бесконечное количество линий.
- Плоскость безгранична, то есть это поверхность, простирающаяся в пространстве без ограничений.
- Две пересекающиеся плоскости определяют линию.
- Линия, имеющая точку в плоскости, не обязательно содержится там. Чтобы линия была частью плоскости, она должна иметь хотя бы две точки на плоскости.
- Бесконечные плоскости пересекают прямую.
- Полуплоскость — это каждая из двух частей, на которые разбивается плоскость при разрезании ее одной из ее прямых.
плоские уравнения
В аналитической геометрии уравнение плоскости — это уравнение, позволяющее математически выразить любую плоскость. Итак, чтобы найти уравнение плоскости, нужна всего лишь точка и два линейно независимых вектора, принадлежащих этой плоскости.

Однако, как мы видели выше при объяснении понятия плана, существует несколько способов определения плана. Ну, точно так же существуют и разные способы аналитического выражения плана.
Таким образом, всеми типами уравнений плоскости являются: векторное уравнение , параметрические уравнения , неявное (или общее) уравнение и каноническое (или сегментное) уравнение плоскости.
Затем мы подробно увидим объяснение и формулы всех уравнений плана.
Векторное уравнение плоскости
Рассмотрим точку и два направляющих вектора плоскости:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Формула векторного уравнения плоскости :
![]()
Или эквивалент:
![]()
Золото
![]()
И
![]()
два скаляра, то есть два действительных числа.
Параметрические уравнения плоскости
Формула параметрического уравнения плоскости :
![]()
Золото:
-
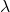
И
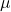
два скаляра, то есть два действительных числа.
-
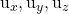
являются компонентами одного из двух направляющих векторов плана
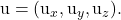
-
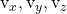
являются компонентами другого направляющего вектора плана
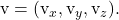
Неявное или общее уравнение плоскости
Рассмотрим точку и два направляющих вектора плоскости:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Неявное, общее или декартово уравнение плоскости получается путем решения следующего определителя и присвоения результата, равного 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Таким образом, неявное или общее уравнение полученного плана будет следующим:
![]()
Этот тип уравнения плоскости также называют декартовым уравнением плоскости.
Каноническое или сегментное уравнение плоскости
Формула канонического или сегментного уравнения плоскости имеет следующий вид:
![]()
Золото:
-

— это точка пересечения плоскости и оси X.
-

— это точка пересечения плоскости и оси Y.
-

Здесь плоскость пересекает ось Z.
Каноническое уравнение (или сегментное уравнение) плоскости также можно получить из ее общего уравнения:
![]()
Сначала решаем коэффициент D из уравнения:
![]()
Затем разделим все уравнение плана на значение параметра D, изменившего знак:
![]()
![]()
И, используя свойства дробей, приходим к следующему выражению:
![]()
Поэтому мы выводим из этого выражения формулы, позволяющие непосредственно вычислять члены канонического или сегментного уравнения плоскости:
![]()
следовательно, чтобы можно было составить этот вариант уравнений плана, коэффициенты А, В и С должны быть отличны от нуля, что позволяет избежать неопределенности дробей.
Взаимное положение двух плоскостей
В аналитической геометрии существует только три возможных относительных положения между двумя плоскостями: секущие плоскости, параллельные плоскости и совпадающие плоскости.
- Пересекающиеся плоскости : две плоскости пересекаются, если они пересекаются только по одной линии.
- Параллельные плоскости : Две плоскости параллельны, если они не пересекаются ни в одной точке.
- Совпадающие плоскости : Две плоскости совпадают, если все они имеют общие точки.
пересекающиеся плоскости

параллельные плоскости

совпадающие плоскости

Кроме того, если две пересекающиеся плоскости пересекаются под углом 90°, это две взаимно перпендикулярные плоскости .
Угол между двумя плоскостями
Угол между двумя плоскостями равен углу, образованному векторами нормалей к указанным плоскостям. Поэтому для нахождения угла между двумя плоскостями вычисляется угол, образованный их векторами нормалей, поскольку они эквивалентны.
Итак, раз уж мы точно знаем, из чего состоит угол между двумя плоскостями, давайте посмотрим формулу расчета угла между двумя плоскостями в пространстве, которая выводится из формулы угла между двумя векторами:
Учитывая общее (или неявное) уравнение двух разных плоскостей:
![]()
![]()
Нормальный вектор каждой плоскости:
![]()
![]()
А угол, образованный этими двумя плоскостями, определяется путем вычисления угла, образованного их векторами нормалей, по следующей формуле:
![]()
Очевидно, что после того, как мы вычислили косинус угла, образованного двумя плоскостями по формуле, мы должны обратить косинус, чтобы найти значение указанного угла.
С другой стороны, когда две плоскости перпендикулярны или параллельны, нет необходимости применять формулу, поскольку угол между двумя плоскостями можно определить напрямую:
- Угол между двумя параллельными плоскостями равен 0°, так как их нормали имеют одинаковое направление.
- Угол между двумя перпендикулярными плоскостями равен 90°, поскольку их векторы нормалей также перпендикулярны (или ортогональны) друг другу и, следовательно, образуют прямой угол.