В этой статье мы объясним, что такое периодичность функции. Кроме того, вы увидите несколько примеров периодических функций. Наконец, проанализируем период тригонометрической функции, поскольку он является одной из важнейших ее характеристик.
Что такое периодичность функции?
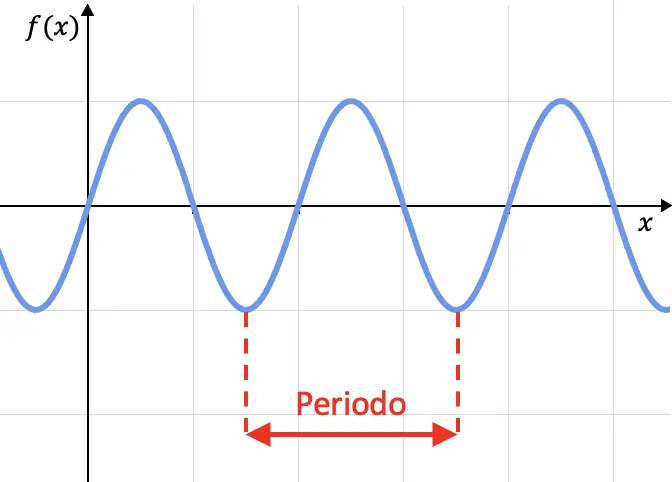
Периодичность функции – это характеристика функций, которые циклически повторяют свои значения, то есть функция является периодической, если ее график повторяется через каждый определенный интервал. Этот интервал называется периодом.
Математически функция называется периодической, если она выполняется только
![]()
для любого значения независимой переменной x.
![]()
Где T — период периодической функции i k целое число.
Примеры периодичности функций
Познакомившись с понятием периодичности функции, мы увидим несколько примеров того, как вычислить периодичность функции.
Пример 1
Определите, является ли следующая функция периодической:
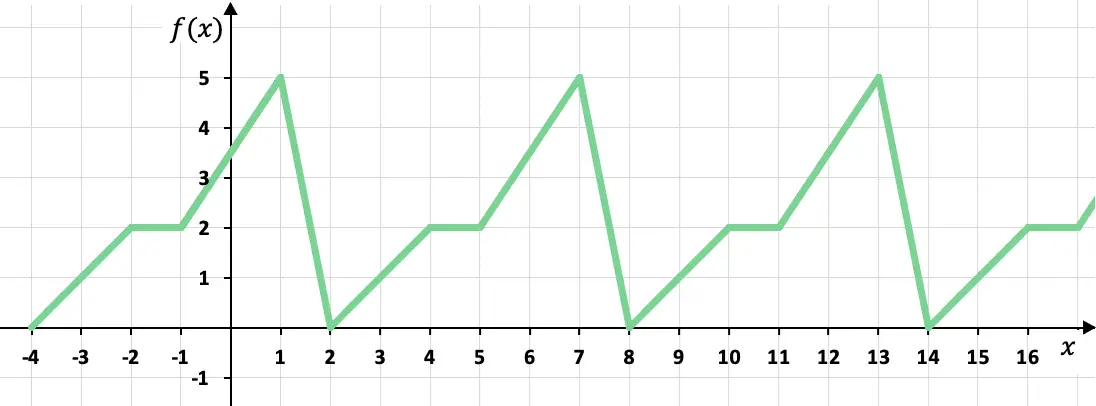
Эта кусочно определенная функция является периодической функцией, так как значения ее графика циклически повторяются. Точнее, функция принимает одно и то же значение каждые шесть х, следовательно, период функции равен 6.
![]()
Пример 2
Найдите периодичность следующей функции:
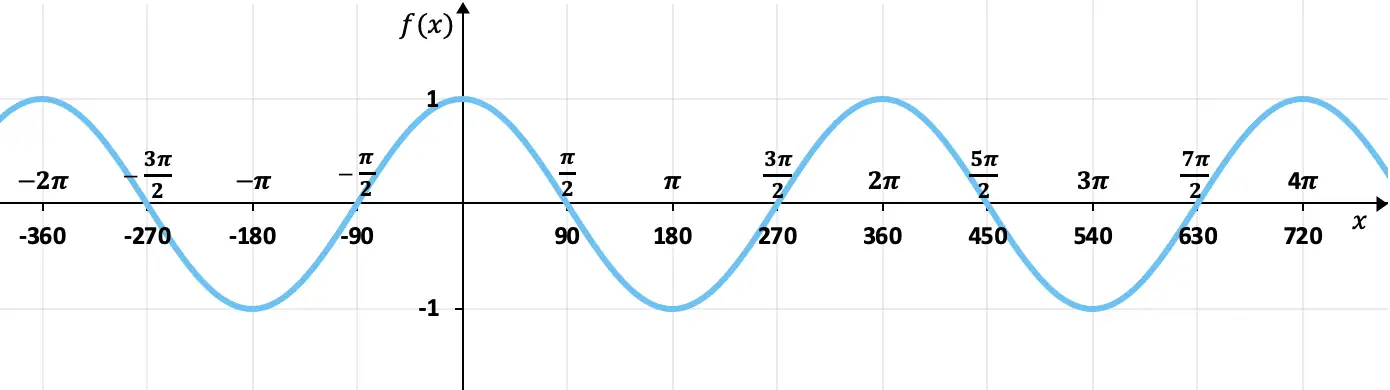
Эта функция соответствует графическому представлению тригонометрической функции, точнее функции косинуса.
Как мы видим из графика, функция периодически повторяет свои значения, поэтому является периодической функцией. Кроме того, между пиком и пиком волны есть пространство в 2π (или 360°), то есть это период функции.
![]()
Периодичность тригонометрических функций
Периодичность и тригонометрические функции тесно связаны, фактически одной из основных характеристик этого типа функций является то, что большинство тригонометрических функций являются периодическими.
Далее мы изучим периодичность 3-х основных тригонометрических функций: синуса, косинуса и тангенса.
Период синусоидальной функции
Выражение для синусоидальной функции выглядит следующим образом:
![]()
В этом случае нет необходимости строить график функции, чтобы найти ее период, но его можно вычислить, просто применив следующую формулу:
![]()
Кроме того, синусоидальная функция имеет особенность: если мы изменяем ее период, мы также изменяем форму ее графика. Посмотреть, как значение периода влияет на его графическое представление, можно по следующей ссылке:
➤ См.: График синусоидальной функции.
Период функции косинуса
Алгебраическое выражение для косинуса выглядит следующим образом:
![]()
Как и в случае с синусом, период функции косинуса можно найти непосредственно по следующей формуле:
![]()
Значение периода косинуса полностью определяет его график, нажмите на следующую ссылку и узнайте почему:
➤ См.: График функции косинуса.
Период касательной функции
Тангенсальная функция описывается математически:
![]()
Период тангенса рассчитывается по той же формуле, что и для синуса и косинуса:
![]()
Однако график функции тангенса отличается от графика синуса и косинуса, поскольку он также имеет периодически повторяющиеся асимптоты. Увидеть эту и другие особенности этой тригонометрической функции можно по следующей ссылке:
➤ См.: График функции тангенса.