Как вычислить определитель матрицы 2×2

На этой странице вы узнаете, что такое определитель матрицы 2×2. Кроме того, вы найдете пошаговые примеры решения и упражнения по решению определителей 2-го порядка, чтобы вы могли в совершенстве попрактиковаться и понять их.

Что такое определитель 2×2?

Определитель порядка 2 — это матрица размерности 2 × 2 , представленная вертикальной чертой с каждой стороны матрицы. Например, если у нас есть следующая матрица:

$\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}$

Определитель матрицы A представляется следующим образом:

$\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}$

Как видите, написать определитель квадратной матрицы 2×2 несложно. Теперь посмотрим, как он рассчитывается:

Как решить определитель второго порядка?

Чтобы вычислить определитель матрицы 2х2, нам нужно перемножить элементы главной диагонали и вычесть произведение второстепенной диагонали.

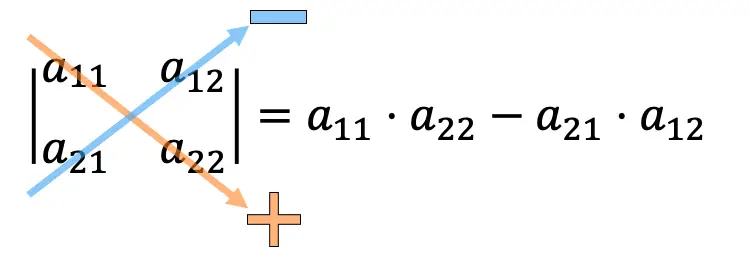
пример вычисления определителя матрицы 2х2

Примеры расчета определителей 2×2:

$\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}$

$\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}$

Решенные задачи определителей матриц 2×2

Упражнение 1

Вычислите следующий определитель 2×2:

посмотреть решение

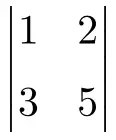
Чтобы составить определитель 2×2, необходимо перемножить элементы главной диагонали и вычесть произведение второстепенной диагонали:

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}$

Упражнение 2

Решите следующий определитель размерности 2×2:

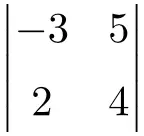
упражнения решаются поэтапно определителей 2х2

посмотреть решение

Чтобы найти решение определителя 2-го порядка, необходимо перемножить элементы главной диагонали и вычесть произведение второстепенной диагонали:

$\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}$

Упражнение 3

Найдите решение следующего определителя второго порядка:

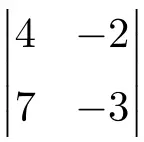
упражнение поэтапное решение определителя матрицы 2x2

посмотреть решение

Чтобы найти решение определителя размерности 2, необходимо перемножить элементы главной диагонали и вычесть произведение второстепенной диагонали:

$\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}$

Упражнение 4

Вычислите следующий определитель 2×2:

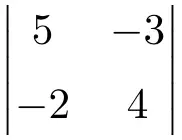
как решить определитель матрицы 2х2, упражнение решено пошагово

посмотреть решение

Чтобы вычислить определители матриц 2х2, нам нужно перемножить элементы главной диагонали и вычесть произведение второстепенной диагонали:

$\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}$

Упражнение 5

Определите результат следующего определителя 2×2:

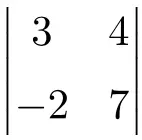
Решенное упражнение на пошаговое разрешение определителя матрицы второго порядка

посмотреть решение

Чтобы найти решение определителя 2х2, нам нужно перемножить элементы главной диагонали и вычесть произведение второстепенной диагонали:

$\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}$

Яркий! Теперь вы знаете, как создавать определители размерности 2×2! Теперь вы наверняка уже понимаете, как вычисляется определитель 3х3 , а также как решается определитель матрицы 4х4 .

Как вычислить определитель матрицы 2х2

Что такое определитель 2×2?

Как решить определитель второго порядка?

Примеры расчета определителей 2×2:

Решенные задачи определителей матриц 2×2

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Оставьте комментарий Отменить ответ