Обратная функция пропорциональности

На этой странице объясняется, что такое функции обратной пропорциональности и как их построить на графике. Кроме того, вы найдете все характеристики этого типа функции, способы вычисления ее области определения, а также несколько примеров и упражнений, решаемых шаг за шагом на практике.

Что такое обратная функция пропорциональности?

Таким образом, обратные функции пропорциональности всегда состоят из дробей с многочленом первой степени в знаменателе. Следовательно, они являются разновидностью рациональной функции.

Примеры обратных функций пропорциональности:

В целом

обычно является независимой переменной и

зависимая переменная или, другими словами, переменная

зависит от

С другой стороны, коэффициент пропорциональности (член числителя) может быть положительным или отрицательным, и его знак указывает на увеличение или уменьшение функции:

• Если константа

  

  отрицательна, функция возрастает.

• Вместо этого, если константа

  

  положительна, функция убывает.

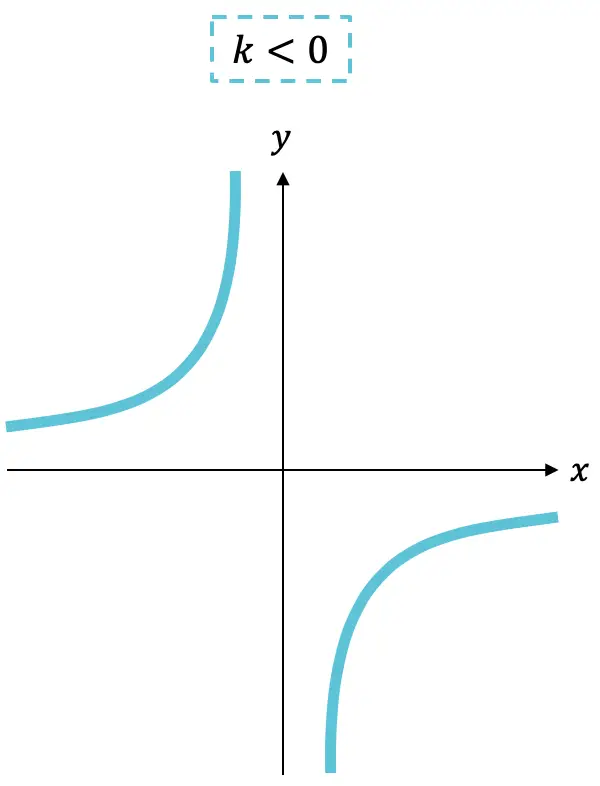
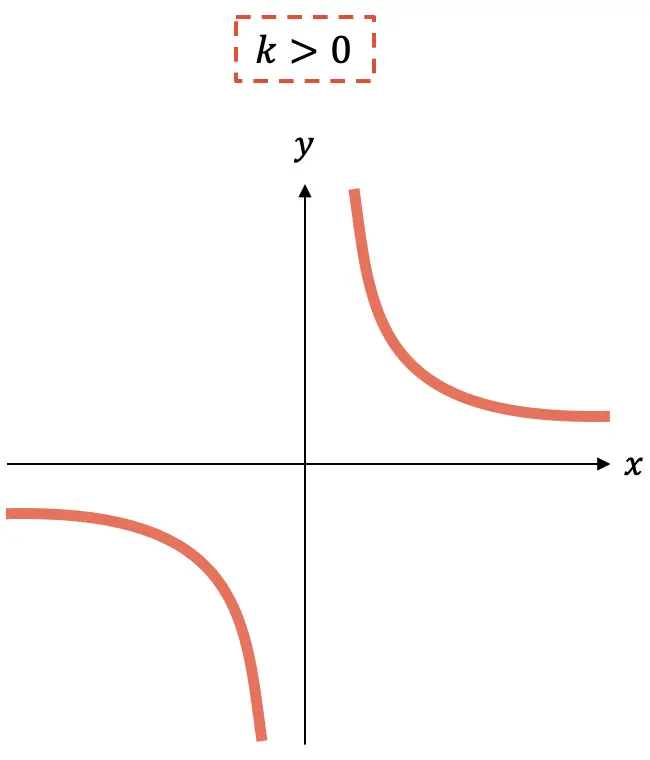
Как видите, график обратной функции пропорциональности всегда состоит из двух гипербол , которые в зависимости от знака k будут находиться в том или ином квадранте.

Область определения обратной функции пропорциональности

Будучи разновидностью рациональной функции, областью действия обратной функции пропорциональности являются все действительные числа, кроме тех, которые исчезают из знаменателя . Потому что знаменатель никогда не может быть равен нулю, потому что это привело бы к бесконечности.

В качестве примера определим область определения следующей обратной функции пропорциональности:

Чтобы узнать, когда знаменатель равен нулю, мы должны приравнять его выражение к 0 и решить уравнение:

Таким образом, когда x примет значение 1, знаменатель будет равен нулю и мы получим неопределенность. Таким образом, областью определения функции являются все действительные числа минус

Как построить график функции обратной пропорциональности

На примере мы увидим, как построить график обратной функции пропорциональности.

• Представим на графике следующую функцию:

Первое, что нам нужно сделать, это найти область определения функции. Поскольку это дробь, знаменатель никогда не может быть равен 0, потому что тогда это приведет к бесконечности. Следовательно, домен будет состоять из x, за исключением случаев, когда знаменатель отменяется.

Поэтому мы устанавливаем знаменатель равным 0, чтобы увидеть, какой x не принадлежит области определения:

Следовательно, областью определения функции являются все числа, кроме 2:

Как только мы узнаем, какой номер не принадлежит домену, мы создаем таблицу значений. Для представления функций обратной пропорциональности необходимо вычислить 3 или 4 точки слева и 3 или 4 точки справа от числа, не принадлежащего области (2):

Теперь представим точки на графике :

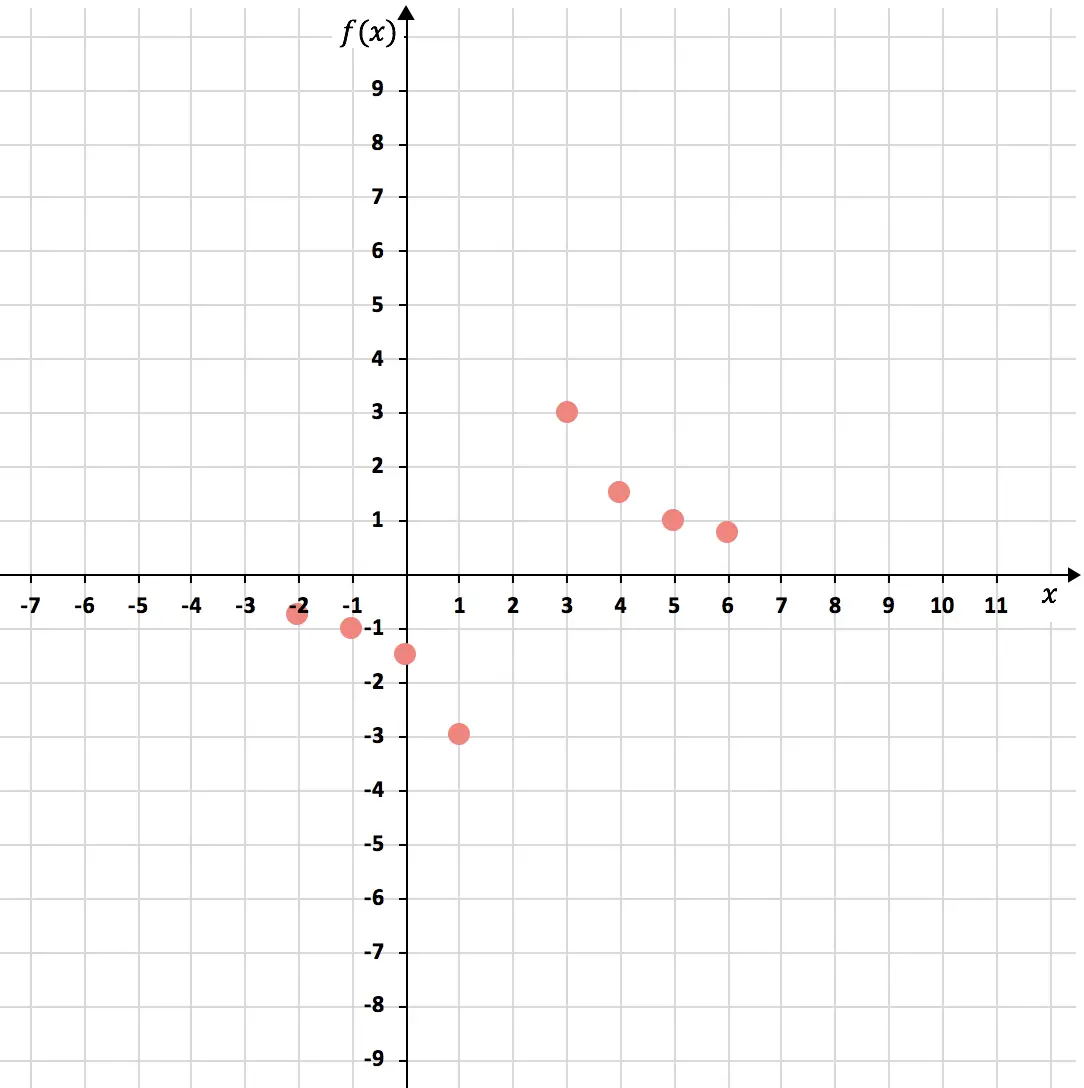
И, наконец, соединяем точки, образуя две гиперболы обратной функции пропорциональности. Дополнительно мы удлиняем ветви гипербол, чтобы указать, что они продолжают расти:

Обратите внимание, что функция приближает

, как справа, так и слева. Однако он никогда не достигает 2, он приближается к нему очень близко, но никогда не достигает его. ТАК,

это вертикальная асимптота . Это потому что

не принадлежит области определения функции и, следовательно, функция не существует в этой точке.

И то же самое происходит с горизонтальной осью X. Функция аппроксимирует

но никогда не прикасайтесь к нему. Еще,

является горизонтальной асимптотой .

Это означает, что все обратные функции пропорциональности разрывны, поскольку всегда имеют асимптоту.

Подробнее об асимптотах и пределах функций вы можете узнать на нашем сайте.

Решенные задачи обратных функций пропорциональности

Упражнение 1

Рассчитайте область определения следующей обратной функции пропорциональности:

Функция обратной пропорциональности не будет существовать, если знаменатель равен 0, потому что тогда функция даст ∞. Следовательно, нам нужно установить знаменатель функции равным 0, чтобы увидеть, что x сокращает знаменатель и, следовательно, не принадлежит области определения.

Упражнение 2

Постройте график следующей обратной функции пропорциональности:

Первое, что нужно сделать, это вычислить область определения функции:

Как только мы узнаем, какой номер не принадлежит домену, мы создаем массив значений с помощью функции:

Наконец, представим полученные точки на графике и нарисуем гиперболы, сформировав таким образом обратную функцию пропорциональности:

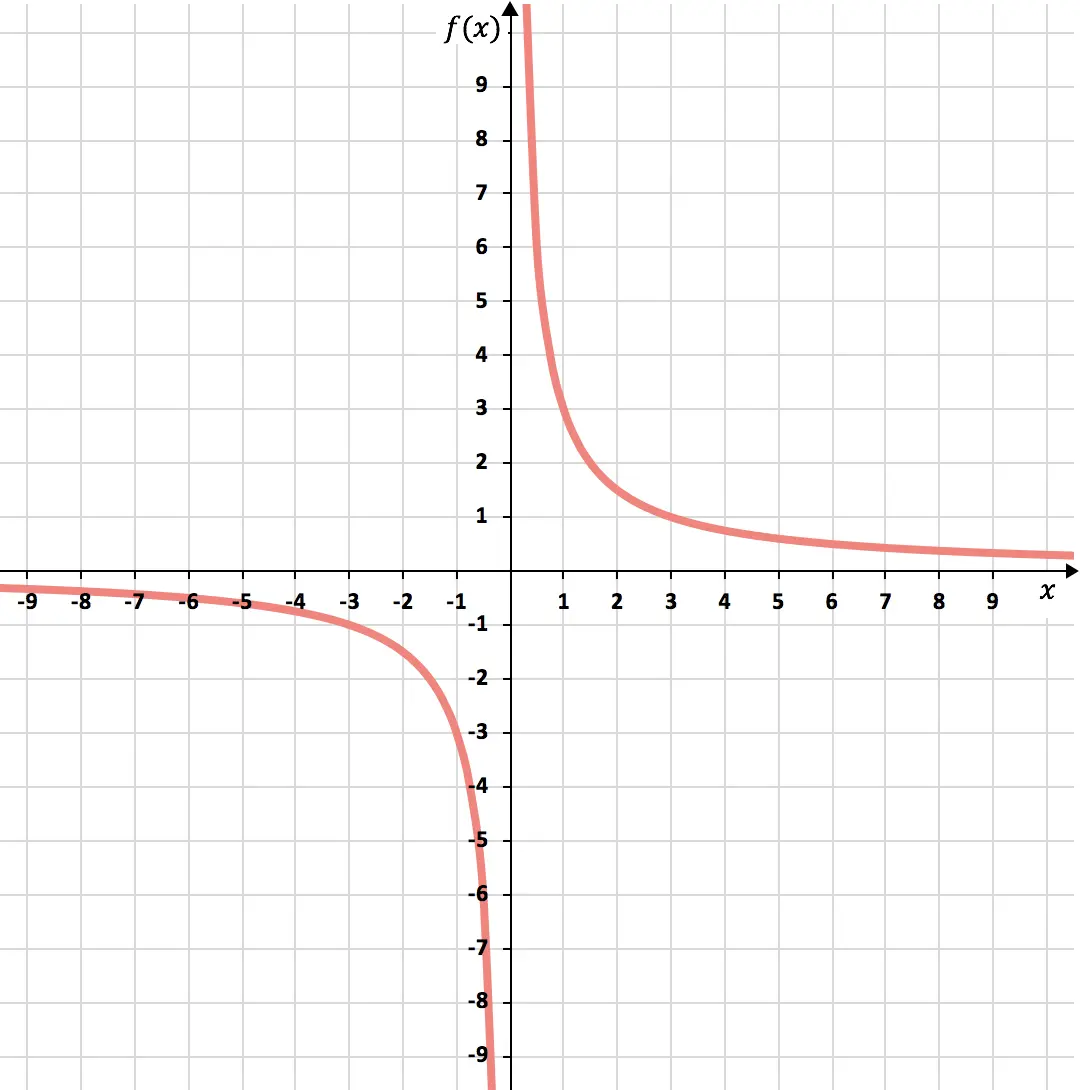
Упражнение 3

Постройте график следующей обратной функции пропорциональности:

Первое, что нужно сделать, это вычислить область определения функции:

Как только мы узнаем область определения функции, мы создадим таблицу значений:

Наконец, представим полученные точки на графике и построим гиперболы, сформировав таким образом обратную функцию пропорциональности:

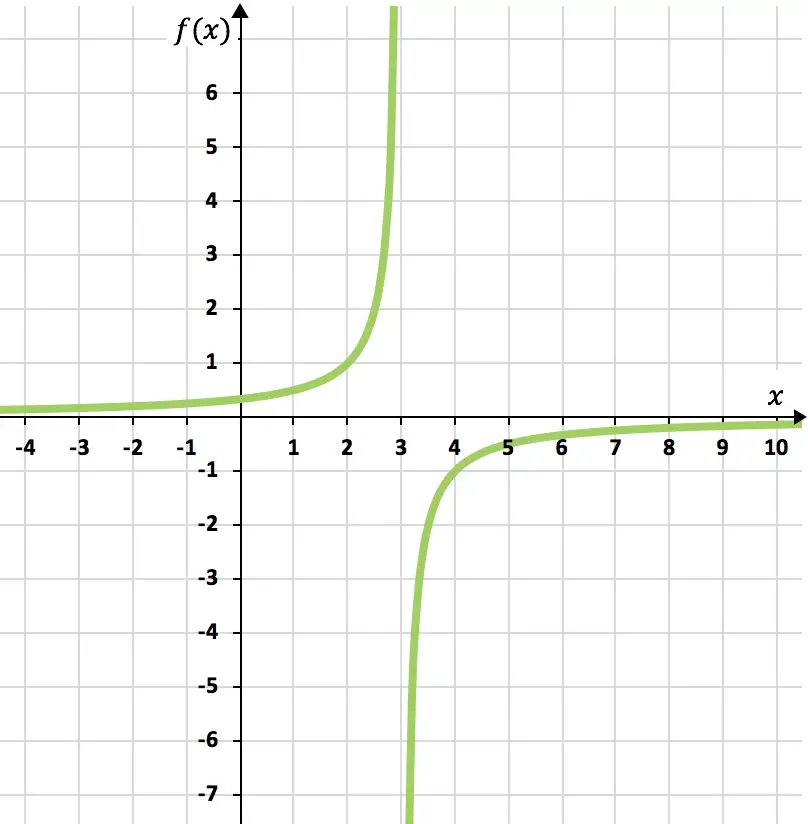
Упражнение 4

Постройте график следующей обратной функции пропорциональности:

Сначала нам нужно вычислить область определения функции:

Как только мы узнаем область определения функции, мы создаем массив значений:

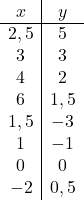
И, наконец, изображаем полученные точки на графике и рисуем гиперболы, образуя таким образом обратную функцию пропорциональности:

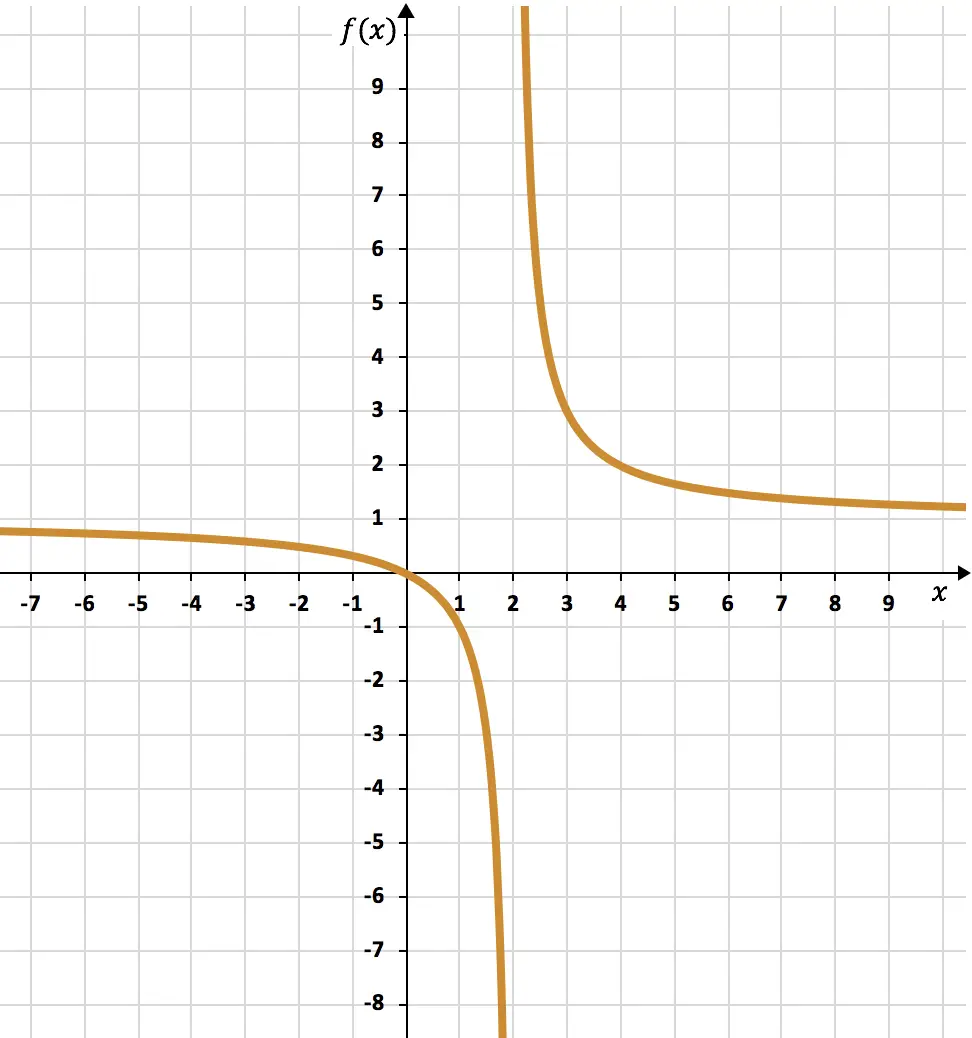
Упражнение 5

Постройте график следующей рациональной функции:

Первое, что нужно сделать, это вычислить область определения функции:

Как только мы узнаем область определения функции, мы создадим таблицу значений:

В завершение просто изобразите полученные точки на графике и нарисуйте гиперболы, образуя таким образом дробную функцию:

Применение обратной функции пропорциональности

Обратная функция пропорциональности появляется во многих случаях в физике и математике.

Например, он используется для описания зависимости между давлением и объемом идеального газа при постоянной температуре k. Эта функция называется законом Бойля-Мариотта (P×V=k) и является примером обратной функции пропорциональности. Очевидно, область определения этой функции ограничивается только положительной ветвью, поскольку отрицательных объемов и давлений нет.

Связь между силой тока и электрическим сопротивлением при постоянной разности потенциалов также определяется обратной функцией пропорциональности. Эта функция известна как закон Ома (V=I×R).