▷ Как найти обратную или обратную функцию (решенные упражнения)

В этой статье мы объясним, что такое обратная (или обратная) функция и как вычислить обратную функцию. Вы также узнаете, как легко узнать, имеет ли функция обратную обратную функцию или нет, а также узнаете о свойствах функций этого типа. Наконец, вы можете попрактиковаться, выполняя пошаговые упражнения на обратные функции.

Что такое обратная функция?

Обратная функция, также называемая обратной функцией, — это функция, областью определения которой является область значений другой функции (исходной функции), а областью определения — областью определения исходной функции. Обратная функция функции f выражается символом f ^-1 .

Следовательно, обратной функцией f(x) является функция, удовлетворяющая следующему условию:

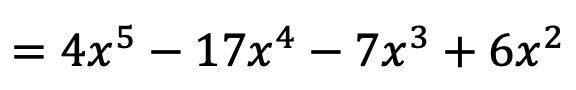
Золото

$f^{-1}$

является обратной функцией

$f.$

Понятие обратной функции также можно определить с помощью композиции функций, поскольку любая функция, составленная из обратной функции, равна тождественной функции:

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

➤ Смотрите: что такое композиция функций?

Итак, если предыдущее уравнение выполняется, это означает, что

$f^{-1}$

— обратная функция (или обратная функция)

$f.$

Пример обратной функции

Учитывая определение обратной функции, давайте решим пример, чтобы лучше понять ее смысл.

Определите, являются ли следующие функции обратными друг другу:

$f(x)=2x+1\qquad g(x)=\cfrac{x-1}{2}$

Если две функции являются обратными друг другу, будут выполнены следующие 2 условия:

$(f \circ g)(x) = x \qquad \qquad (g \circ f)(x) = x$

Итак, давайте проверим, выполняются ли оба уравнения. Сначала мы проверяем

$(f \circ g)(x) = x:$

$\begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}$

➤ Если вы не понимаете только что выполненный расчет, перейдите по ссылке выше, чтобы узнать, каков состав функций? , мы объясним, как решить этот тип операции с функциями.

Так что

$(f \circ g)(x) = x$

да, это осуществимо. ✅

Теперь проверим равенство

$(g \circ f)(x) = x :$

$\begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}$

И условие обратимости

$(g \circ f)(x) = x$

это тоже осуществимо. ✅

В заключение, поскольку оба уравнения выполняются, эти две функции являются обратными друг другу.

Ниже вы можете увидеть графики обеих функций. Обратите внимание, что графики двух обратных функций симметричны относительно биссектрисы первого и третьего квадрантов:

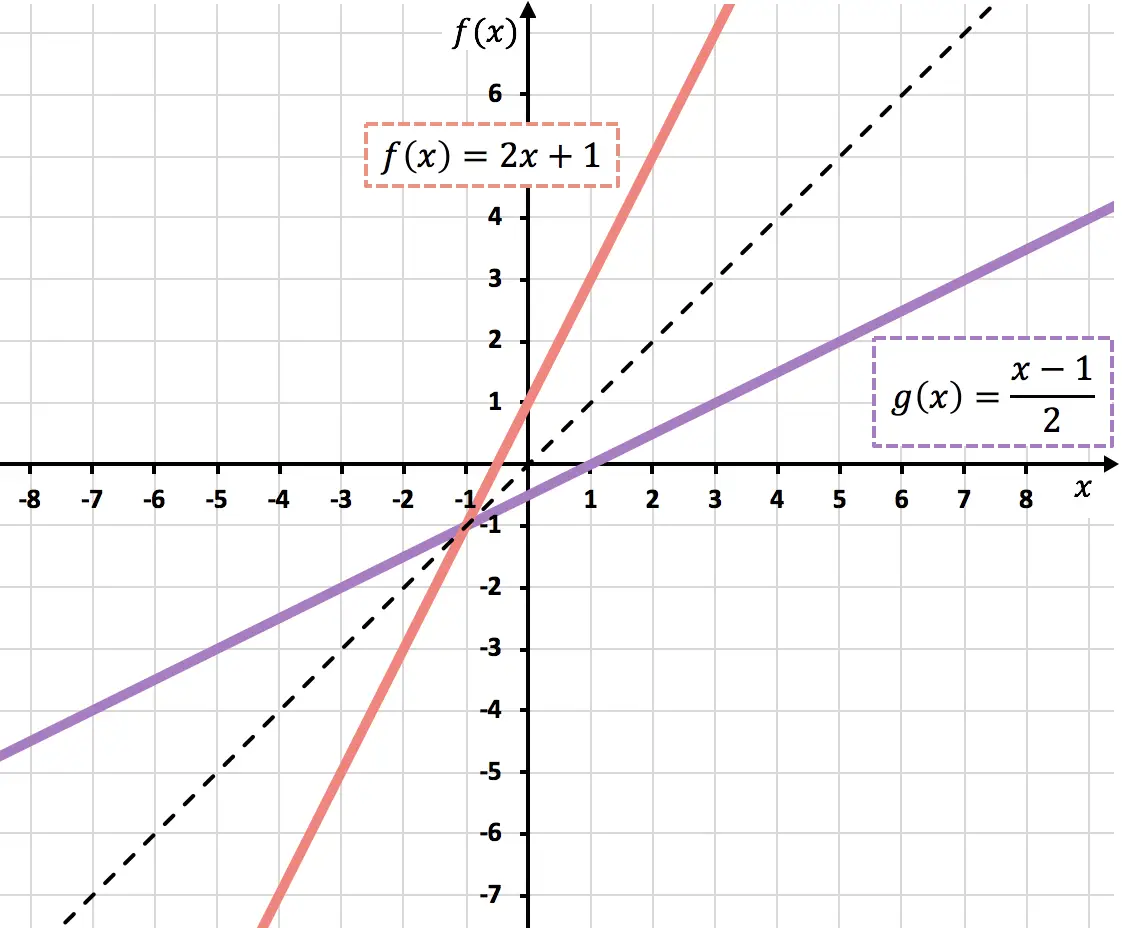
Как определить, имеет ли функция обратную?

Функция имеет обратную функцию, если она является инъективной функцией , то есть если каждое значение во всей ее области определения соответствует одному значению в своем интервале.

Показательная функция с обратной функцией

Квадратичная функция без обратной функции

Например, левая экспоненциальная функция имеет обратную функцию, поскольку каждый x соответствует одному значению f(x) . С другой стороны, правая квадратичная функция не имеет обратной функции, так как имеет несколько значений x , образы которых равны (например f(1)=f(3)=2) .

Точно так же биективная функция состоит из функции, которая является одновременно инъективной и сюръективной, поэтому любая биективная функция также имеет обратную функцию.

С другой стороны, следует иметь в виду, что обратная функция — это не то же самое, что мультипликативная обратная функция , а скорее два разных понятия. Чтобы найти мультипликативную обратную функцию, просто вычислите одно соответствие по указанной функции.

$f^{-1}(x) \neq \cfrac{1}{f(x)}$

В следующем разделе мы увидим, как определить обратную функцию.

Как найти обратную функцию

Для вычисления обратной функции необходимо выполнить следующие действия:

Замените f(x) на y .
Измените все x на y и наоборот.
Очистите переменную y .
Замените переменную y на f ^-1 (x) . Обратная функция — это выражение, найденное для f ^-1 (x) .

Чтобы вы могли увидеть, как именно рассчитывается обратная функция, в качестве примера определим обратную функцию:

$f(x) =4x+5$

Прежде всего нам необходимо заменить

$f(x)$

Для

$y$

$y=4x+5$

Теперь мы все меняем

$x$

функции по

$y$

, и наоборот:

$y= 4x+5 \quad \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \quad x= 4y+5$

Затем мы очищаем переменную

$y:$

$x=4y+5$

$x-5=4y$

$\cfrac{x-5}{4}=y$

$y=\cfrac{x-5}{4}$

И, наконец, обратная функция

$f(x)$

— алгебраическое выражение, которое мы получили, выделив

$y:$

$\bm{f^{-1}(x) = } \cfrac{\bm{x-5}}{\bm{4}}$

Решенные упражнения обратной функции

Ниже мы подготовили несколько пошаговых упражнений по обратной функции, чтобы вы могли попрактиковаться.

👉 Помните, что если вы не понимаете, как решить упражнение или хотите, чтобы мы решили за вас задачу, вы можете написать нам в комментариях!

Упражнение 1

Проверьте, являются ли следующие две функции обратными (или взаимными) или нет:

$f(x)=3x-7\qquad g(x)=\cfrac{x+7}{3}$

Посмотреть решение

Чтобы две функции были обратными друг другу, должно выполняться следующее:

$(f \circ g)(x)=x \qquad \qquad (g \circ f)(x)=x$

Поэтому необходимо проверить, выполняются ли оба условия. Сначала мы проверяем

$(f \circ g)(x)=x :$

$\begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}$

Еще,

$(f \circ g)(x) = x$

да, это осуществимо. ✅

Теперь проверим другой состав функций

$(g \circ f)(x)=x :$

$\begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}$

Посредством чего

$(g \circ f)(x) = x$

это тоже осуществимо. ✅

Как это происходит

$(f \circ g)(x)=x$

$(g \circ f)(x)=x$

, эти две функции являются обратными друг другу.

Упражнение 2

Вычислите обратную (или обратную функцию) следующей полиномиальной функции первой степени:

$f(x)=-2x-3$

Посмотреть решение

Первое, что нужно сделать, чтобы обратить функцию, — это заменить член

$f(x)$

Для

$}y:$

$y=-2x-3$

Теперь мы меняем

$x$

$y$

, и наоборот:

$y=-2x-3 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =-2y-3$

И тогда мы выпускаем

$y:$

$x =-2y-3$

$x +3=-2y$

$\cfrac{x +3}{-2}=y$

$y = \cfrac{x +3}{-2}$

Нам уже удалось выпустить

$y$

. Следовательно, обратная функция

$f(x)$

Восток:

$\bm{f^{-1}(x) = -} \cfrac{\bm{x+3}}{\bm{2}}$

Упражнение 3

Инвертируйте следующую квадратичную полиномиальную функцию:

$f(x)=x^2-1$

Посмотреть решение

Чтобы найти обратную функцию, мы будем следовать процедуре, которую мы видели выше. Итак, мы позвоним

$y$

к функции

$f(x):$

$y=x^2-1$

Во-вторых, мы модифицируем

$x$

для

$y$

, и наоборот:

$y=x^2-1 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =y^2-1$

И, наконец, изолируем переменную

$y:$

$x =y^2-1$

$x+1=y^2$

$\sqrt{x+1}=y$

$y=\pm \sqrt{x+1}$

Однако в этом случае полученная функция имеет два образа для каждого элемента своей области определения (положительный образ и отрицательный образ). Следовательно, не существует обратной функции проблемной функции.

Упражнение 4

Определите обратную функцию (или обратную функцию) следующей рациональной функции:

$\displaystyle f(x)=\frac{x-1}{2x+3}$

Посмотреть решение

Сначала заменим

$f(x)$

Для

$y:$

$y=\cfrac{x-1}{2x+3}$

Теперь мы меняем

$x$

числитель и знаменатель

$y$

, и наоборот:

$y=\cfrac{x-1}{2x+3} \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x=\cfrac{y-1}{2y+3}$

И тогда мы выпускаем

$y:$

$x=\cfrac{y-1}{2y+3}$

Выражение

$2y +3$

делит всю правую часть уравнения, поэтому мы можем умножить ее, умножив всю левую часть уравнения:

$x\cdot (2y+3)=y-1$

$2yx+3x=y-1$

Мы ставим все условия

$y$

с одной стороны уравнения, а остальные члены с другой стороны:

$2yx-y=-3x-1$

Чтобы очистить

$}y$

, мы извлекаем общий множитель из левой части уравнения:

$y(2x-1)=-3x-1$

И как почтальон

$(2x-1)$

состоит в том, чтобы умножить всю левую часть уравнения, мы можем сделать это, разделив всю правую часть:

$y=\cfrac{-3x-1}{2x-1}$

Нам уже удалось выпустить

$y$

. Итак, обратная функция

$f(x)$

Восток:

$\bm{f^{-1}(x)=} \cfrac{\bm{-3x-1}}{\bm{2x-1}}$

Свойства обратной функции

Обратная функция имеет следующие характеристики:

Обратная функция единственна, то есть если функция обратима, то для этой функции существует только одна обратная функция.

Областью определения обратной функции является диапазон (или диапазон) исходной функции.

Аналогично, путь обратной функции эквивалентен области определения исходной функции.

Любая функция, составленная из обратной функции, дает тождественную функцию (x).

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

График функции и график обратной функции симметричны относительно биссектрисы первого и третьего квадрантов.

Обратная функция равна исходной функции:

$\left(f^{-1}\right)^{-1}=f$

Инвертирование составной функции эквивалентно вычислению обратной каждой функции отдельно и последующему составлению обратных функций.

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Функция одновременно непрерывна со своей обратной функцией, или, другими словами, если функция непрерывна, то и ее обратная функция будет непрерывной.

Если функция дифференцируема и производная никогда не исчезает
$f'(x)\neq 0$

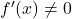
, то его обратная функция также будет дифференцируемой.

Кроме того, производную обратной функции можно вычислить, применив теорему об обратной функции , формула которой:

$\left(f^{-1}\right)'(y)=\cfrac{1}{f'(x)}$

Обратная (или обратная) функция

Что такое обратная функция?

Пример обратной функции

Как определить, имеет ли функция обратную?

Как найти обратную функцию

Решенные упражнения обратной функции

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Свойства обратной функции

Оставьте комментарий Отменить ответ