На этой странице вы найдете объяснение нулевой матрицы, также называемой нулевой матрицей. Вы также увидите на примерах, что значения ее элементов не зависят от размерности матрицы, и, наконец, найдете все свойства матрицы этого типа.
Что такое нулевая матрица?
Нулевая матрица (или нулевая матрица) — это матрица, все элементы которой равны нулю (0).
Следовательно, по определению нулевой матрицы, эта матрица может иметь все возможные размерности, пока все ее числа равны нулю. Посмотрите на следующие примеры:
Примеры нулевых матриц
Пример нулевой матрицы 2 × 2
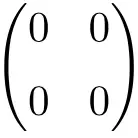
Пример нулевой матрицы 3 × 3
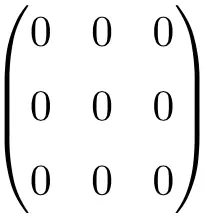
Пример нулевой матрицы 4 × 4
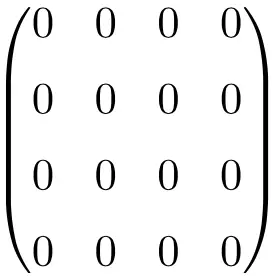
Теперь вам может показаться, что именно эта конкретная матрица не имеет значения, поскольку это просто матрица, полная нулей. Однако в математике, а точнее в области линейной алгебры, это очень полезная матрица, поскольку она значительно упрощает вычисления.
Свойства нулевой матрицы
Нулевые (или нулевые) матрицы имеют следующие характеристики:
- Нулевая матрица является нейтральным элементом операции сложения матриц, поэтому:
![]()
- Умножение матриц обладает мультипликативным свойством нуля, то есть произведение любой матрицы, умноженной на нулевую матрицу, равно 0.
![]()
- Если матрица квадратная, нулевая матрица одновременно симметрична и антисимметрична .
- Нулевая матрица — единственная матрица, ранг которой равен нулю.
- Определитель нулевой матрицы всегда равен 0, поэтому этот тип матрицы не имеет обратной (это сингулярная матрица).
- Очевидно, что нулевая матрица является примером нильпотентной матрицы .