Регулярная матрица

На этой странице вы увидите, что такое нормальная матрица, а также примеры нормальных матриц. Кроме того, вы найдете свойства этого типа матриц и упражнения, решаемые шаг за шагом.

Что такое нормальная матрица?

Обычное определение массива:

Нормальная матрица — это комплексная матрица, умноженная на свою сопряженную транспонированную матрицу , равна произведению сопряженной транспонированной матрицы на себя.

$A\cdot A^*=A^*\cdot A$

Золото

$A^*$

— сопряженная транспонированная матрица

$A$

Однако, если это матрицы действительных чисел , предыдущее условие означает, что матрица коммутирует с ее транспонированием, то есть:

$A\cdot A^t=A^t\cdot A$

Потому что, очевидно, сопряженная транспонированная матрица реальной матрицы — это просто транспонированная (или транспонированная) матрица.

Примеры нормальных матриц

Пример с комплексными числами

Следующая комплексная квадратная матрица размерности 2×2 является нормальной:

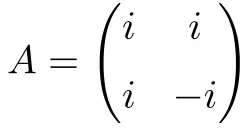
пример нормальной матрицы с комплексными числами размерности 2x2

Демонстрация его нормальности прикреплена ниже:

$\displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

$\displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

Пример с действительными числами

Следующая квадратная матрица с действительными числами второго порядка также является нормальной:

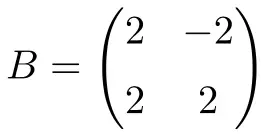
пример нормальной матрицы с действительными числами размерности 2x2

В этом случае, поскольку в ней есть только действительные числа, для доказательства ее нормальности достаточно убедиться в коммутативности матрицы с ее транспонированием:

$\displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

$\displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

Свойства нормальных матриц

Нормальные матрицы имеют следующие характеристики:

Все нормальные матрицы являются диагонализуемыми матрицами.

Каждая унитарная матрица также является нормальной матрицей.

Аналогично, эрмитова матрица является нормальной матрицей.

Аналогично, антиэрмитова матрица является нормальной матрицей.

Если A — нормальная матрица, то собственные значения (или собственные значения) сопряженной транспонированной матрицы A* являются сопряженными собственными значениями A.

$\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i$

$\displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i$

В нормальных матрицах собственные векторы (или собственные векторы), связанные с разными собственными значениями, ортогональны.

Если матрица составлена только из действительных чисел и симметрична , она одновременно является нормальной матрицей.

Аналогично, антисимметричная действительная матрица также является нормальной матрицей.

Наконец, любая ортогональная матрица, составленная из действительных чисел, также является нормальной матрицей.

Решенные упражнения для нормальных матриц

Упражнение 1

Убедитесь, что следующая комплексная матрица размерности 2 × 2 является нормальной:

$\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}$

посмотреть решение

Чтобы показать, что матрица нормальна, мы должны сначала вычислить ее сопряженное транспонирование:

$\displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}$

А теперь делаем проверку, умножая матрицу А на матрицу А* в обоих возможных направлениях:

$\displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

Результат обоих умножений одинаков, поэтому матрица A нормальна.

Упражнение 2

Покажите, что следующая действительная матрица размера 2 × 2 является нормальной:

$\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}$

посмотреть решение

Поскольку в этом случае мы имеем дело со средой, содержащей только действительные числа, достаточно убедиться, что матричное произведение матрицы A и ее транспонирования дает один и тот же результат независимо от направления умножения:

$\displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

$\displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

Результат обоих произведений один и тот же, поэтому матрица A является нормальной.

Упражнение 3

Определите, является ли нормальной следующая матрица комплексных чисел второго порядка:

$\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}$

посмотреть решение

Чтобы проверить, что матрица нормальна, надо сначала вычислить ее сопряженное транспонирование:

$\displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}$

А теперь проверим, переключаема ли матрица A и сопряженное с ней транспонирование:

$\displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

Результат обоих умножений одинаков, поэтому матрица A нормальна.

Упражнение 4

Убедитесь, что следующая действительная матрица размерности 3×3 является нормальной:

$\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}$

посмотреть решение

Поскольку матрица полностью состоит из вещественных элементов, достаточно убедиться, что матричное произведение между матрицей A и ее транспонированием не зависит от направления умножения:

$\displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

$\displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

Результат обоих произведений один и тот же, поэтому матрица A является нормальной.

Упражнение 5

Определите, является ли следующей комплексная матрица порядка 3×3 нормальной:

$\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

посмотреть решение

Сначала мы вычисляем сопряженное транспонирование матрицы:

$\displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

Теперь нам нужно выполнить матричные умножения между матрицей A и ее сопряженной транспонированной матрицей в обоих возможных направлениях. Однако сопряженная транспонированная матрица A равна самой матрице A, поэтому она является эрмитовой матрицей. И поэтому из свойств нормальных матриц следует, что А — нормальная матрица , потому что каждая эрмитова матрица — нормальная матрица.

Что такое нормальная матрица?

Примеры нормальных матриц

Пример с комплексными числами

Пример с действительными числами

Свойства нормальных матриц

Решенные упражнения для нормальных матриц

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Оставьте комментарий Отменить ответ