Что такое число Эйлера? -Маторство

Число Эйлера (также известное как константа Эйлера) — важное и существенное математическое число в различных областях математики, включая теорию чисел, топологию, теорию групп и теорию функций. Он обозначается греческой буквой «е», а его приблизительное значение составляет 2,71828.

Число e следует из формулы показательной функции и является фундаментальным числом в теории комплексных чисел.

Это также натуральное число, которое появляется при решении многих математических задач, включая вычисление вероятности и моделирование процессов роста и распада.

Каково происхождение числа Эйлера?

Число Эйлера названо в честь швейцарского математика Леонарда Эйлера (1707–1783), который был одним из величайших математиков всех времен и считается отцом современной математики.

Эйлер внес ценный вклад во многие области математики, включая теорию чисел, геометрию, исчисление, физику и астрономию.

Именно он впервые определил и использовал число е (называемое числом Эйлера) в своих работах по вычислению и теории логарифмов. Формула Эйлера для комплексных чисел также является одним из его наиболее заметных вкладов в математику.

Как получается это значение?

На самом деле существует несколько методов вычисления числа Эйлера. Однако стоит отметить, что ни один из методов не дает точного результата. Поэтому нумерация его непрерывна и бесконечна, но не повторяется.

Фактически в настоящее время известно более 1 триллиона чисел, составляющих фигуру числа е. Бесконечный ряд, определяющий число Эйлера:

Золотой «!» факториал, который определяется как произведение всех натуральных чисел до этого числа. Например:

5! = 5 4 3 2 1 = 120

Мы можем видеть эту серию графически как сумму серии прямоугольников высоты 1 и уменьшающейся ширины, где ширина каждого прямоугольника равна 1/n!, где n — количество факториалов.

Если мы увеличим количество прямоугольников в сумме, аппроксимация площади под кривой показательной функции будет все ближе и ближе к числу Эйлера.

Подводя итог, можно сказать, что число Эйлера — это число, которое является результатом суммы бесконечного ряда и имеет фундаментальное значение для многих областей математики. Хотя это иррациональное число , его приблизительное значение составляет 2,71828.

Важно помнить, что сам Эйлер применил этот метод для вычисления е с точностью до 18 знаков после запятой.

Другой способ расчета:

Мы можем вычислить приблизительное значение числа Эйлера на прямой, используя ряд конечных членов . Например, если мы возьмем первую бесконечную серию, определенную выше:

Мы можем вычислить приблизительное значение, сложив первые члены ряда. Например, если мы добавим первые 6 терминов:

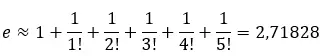
Мы можем построить этот ряд на линии, чтобы увидеть, как он приближается к приблизительному значению 2,71828 .

Графически линию, представляющую число Эйлера, можно нарисовать как серию прямоугольников высотой 1 и уменьшающейся ширины, где ширина каждого прямоугольника равна 1/n!, где n — количество факториалов.

Показательные уравнения с числом Эйлера

Экспоненциальные уравнения с числом Эйлера можно использовать для моделирования широкого спектра явлений в таких науках, как физика, биология, экономика и других. Вот некоторые примеры:

Экспоненциальный рост и упадок

Эта модель описывает скорость, с которой популяция растет или сокращается , или скорость, с которой разрушается токсичное вещество.

Например, если население растет со скоростью 5% в год, его численность можно описать формулой:

P(t) = P0 · e ^0,05t , где P0 — начальная численность популяции.

Модели радиоактивного распада

Эта модель описывает скорость, с которой радиоактивные атомы распадаются с течением времени.

Формула выглядит следующим образом:

N(t) = N0 e ^-λt

где N0 — начальное число атомов, λ — константа, зависящая от радиоактивного материала, а t — время.

Это лишь несколько примеров того, как показательные уравнения с числом Эйлера можно использовать на практике. Есть много других областей, где показательные уравнения полезны и актуальны.

Каковы применения числа Эйлера?

Число Эйлера имеет широкий спектр применения в различных областях математики и естественных наук. Некоторые из полей, в которых используется число e:

Расчет и математический анализ : он используется при изучении показательных и логарифмических функций, а также при решении дифференциальных уравнений.
Теория чисел — используется при изучении распределения простых чисел и при решении задач, связанных с теорией чисел.
Вероятность и статистика : используется при решении задач, связанных с распределением вероятностей и оценкой ожидаемых значений.
Криптография — используется при изучении алгоритмов шифрования и дешифрования.
Физика — используется для решения задач, связанных с термодинамикой, квантовой механикой и статистической физикой.
Химия : используется при решении задач, связанных с химической термодинамикой и химической кинетикой.

Формула Эйлера для комплексных чисел

Формула Эйлера для комплексных чисел устанавливает связь между тригонометрическими и показательными функциями. Формула написана:

Где «e» — основание натуральных логарифмов, «i» — мнимая единица, «x» — действительное число, а «cos» и «sin» — тригонометрические функции косинус и синус соответственно.

Эта формула очень полезна во многих областях математики, включая теорию чисел, теорию функций и теорию сложности, и имеет широкий спектр приложений в технике, физике и экономике.

Практическим примером его использования является представление сигналов и систем в анализе Фурье, в котором периодические сигналы представляются как сумма сложных синусоидальных сигналов.

Формула Эйлера используется для описания того, как эти сложные сигналы соотносятся с реальными тригонометрическими функциями, которые описывают отдельные синусоидальные сигналы.

Число Эйлера и сложные проценты

Сложные проценты — это финансовая концепция , описывающая процесс, посредством которого денежная сумма, называемая основной суммой, приносит проценты по процентам, которые увеличиваются с течением времени.

Другими словами, проценты, полученные от инвестиций, исходят не только от первоначального капитала, но и от процентов, полученных в предыдущие периоды.

Число Эйлера и сложные проценты связаны между собой, поскольку в формуле расчета сложных процентов используется число Эйлера. Формула сложных процентов :

А = П е ^рт

Где A — окончательная сумма, P — основная сумма, r — процентная ставка, t — время, а e — число Эйлера. Таким образом, число Эйлера является важным фактором в математической формулировке расчета сложных процентов.

Пример расчета сложных процентов с конкретными числами:

Предположим, у нас есть инвестиции в размере 1000 евро под процентную ставку 5% в год сроком на 2 года. Формула расчета сложных процентов будет выглядеть так:

A = ^Pert = 1000 e ^{0,05 2} = 1000 1,1025 = 1102,5 евро.

Это означает, что через 2 года наш первоначальный капитал в 1000 евро увеличится до 1102,5 евро благодаря начисленным сложным процентам.

Примеры математических упражнений с числом Эйлера

Вот два примера решенных математических задач , связанных с числом Эйлера:

1. Найдите значение «e ^ix », где x — действительное число:

Тождество Эйлера говорит нам, что e ^ix = cos(x) + i · sin(x). Следовательно, если мы знаем значение x, мы можем вычислить значение e ^ix с помощью тригонометрических функций.

2. Вычислите e^(x ² ) для заданного значения x:

Мы можем использовать ряд Тейлора для вычисления значения e^(x ² ). Ряд Тейлора для ^ex представляет собой бесконечное разложение, которое позволяет вычислять последовательные приближения значения ^ex в зависимости от используемого термина.

Если мы заменим x ² в этом ряду, мы получим ряд Тейлора для e^(x ² ).

Что такое число эйлера?