Бесконечная неопределенность между бесконечностью (∞/∞)

В этой статье мы объясним, как вычислить бесконечность неопределенности между бесконечностью (∞/∞). Примеры этой неопределенности вы найдете со всеми видами функций: полиномиальными, радикальными, показательными функциями и т. д. Кроме того, вы сможете тренироваться с упражнениями, шаг за шагом решающими пределы, которые дают бесконечную неопределенность между бесконечностями.

Как решить бесконечную неопределенность между бесконечными

Когда предел функции дает бесконечность, деленную на бесконечность, это означает, что это неопределенность (или неопределенная форма). Чтобы решить предел функции, которая дает бесконечность неопределенности между бесконечностью, степень полинома числителя необходимо сравнить со степенью полинома знаменателя.

$\displaystyle\lim_{x\to +\infty}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\frac{+\infty}{+\infty}$

Результат неопределенности бесконечности, разделенной на бесконечность, зависит от степени числителя и степени знаменателя дроби:

Если степень многочлена числителя меньше степени многочлена знаменателя, бесконечность неопределенности, разделенная на бесконечность , равна нулю.
Если степень полинома числителя эквивалентна степени полинома знаменателя, бесконечная неопределенность на бесконечности представляет собой частное ведущих коэффициентов двух многочленов.
Если степень многочлена числителя больше степени многочлена знаменателя, бесконечность неопределенности между бесконечностью дает большую или меньшую бесконечность (знак зависит от основных членов двух многочленов).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.» title=»Rendered by QuickLaTeX.com» height=»139″ width=»767″ style=»vertical-align: 0px;»> <h2 class=$ Примеры бесконечной неопределенности между бесконечностью

Давайте посмотрим, как решается неопределенная форма бесконечность между бесконечностью, рассмотрев несколько примеров каждого случая:

степень числителя меньше степени знаменателя

Как мы видели выше, когда степень полинома числителя меньше степени полинома знаменателя, бесконечный неопределенный предел между бесконечностью всегда дает 0.

Пример 1:

$\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

Многочлен числителя имеет вторую степень, а многочлен знаменателя — третьей степени, поэтому решение предела равно 0.

Пример 2:

$\displaystyle \lim_{x \to -\infty} \frac{-7x}{2x^4+3x^2}=\frac{-7\cdot (-\infty)}{2(-\infty)^4}=\frac{+\infty}{+\infty}= \bm{0}$

Полиномиальная функция числителя имеет первую степень, а функция знаменателя — четвертой степени, поэтому предел отрицательной бесконечности равен 0.

степень числителя равна степени знаменателя

Когда степень полинома числителя равна степени полинома знаменателя, неопределенный предел бесконечности на бесконечность вычисляется путем деления старших коэффициентов (коэффициент члена более высокой степени) двух полиномов.

Пример 3:

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

В данном случае два многочлена имеют вторую степень, поэтому необходимо разделить коэффициенты членов более высокой степени, чтобы найти предел на положительной бесконечности.

Пример 4:

$\displaystyle \lim_{x \to -\infty} \cfrac{2x+1}{5x+3} = \cfrac{2(-\infty)}{5(-\infty)}= \cfrac{-\infty}{-\infty} =\cfrac{\bm{2}}{\bm{5}}$

Хотя пределом является ситуация, когда x стремится к минус бесконечности, бесконечная неопределенность между бесконечностью разрешается таким же образом.

Степень числителя больше степени знаменателя

Когда степень полинома числителя больше, чем степень полинома знаменателя, неопределенная форма бесконечности между бесконечностью всегда будет давать бесконечность, а знак бесконечности определяется членами более высокой степени двух полиномов.

Пример 5:

$\displaystyle \lim_{x \to +\infty} \cfrac{x^2+7}{x-2} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

Функция числителя имеет более высокую степень, чем функция знаменателя, поэтому неопределенность бесконечность на бесконечности дает бесконечность. Кроме того, в этом случае и числитель, и знаменатель получают положительную бесконечность, поэтому результат предела также должен быть положительным.

Пример 6:

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

В этой задаче положительная бесконечность получается из числителя, поскольку любой член в квадрате положителен, а отрицательная бесконечность получается из знаменателя. Следовательно, результирующий предел будет отрицательным, поскольку положительное, разделенное на отрицательное, равно отрицательному.

Бесконечная неопределенность между бесконечностью с корнями

Мы только что увидели, как вычислить бесконечную неопределенность между бесконечностью, когда у нас есть полиномиальные функции. Но… насколько бесконечность делится на бесконечность, если у нас есть корни?

Степень иррациональной функции (функции с корнями) — это частное между степенью главного члена и индексом радикала.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

Следовательно, если предел функции с корнями дает неопределенность между бесконечностью , мы должны применить те же правила, объясненные выше, для степеней числителя и знаменателя, но с учетом того, что степень многочлена с корнями вычисляется по-другому.

Посмотрите на следующий пример предела бесконечности функции с радикалами:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

Степень числителя равна 2, а степень знаменателя равна 4 (8/2=4), поэтому предел равен 0, поскольку степень числителя меньше степени знаменателя.

С другой стороны, если степени числителя и знаменателя равны, для вычисления неопределенного предела надо взять главный коэффициент с подкоренным:

$\displaystyle\lim_{x\to +\infty}\frac{6x-5}{\sqrt{9x^2+2x}}=\frac{6(+\infty)}{\sqrt{9(+\infty)^2}}=\frac{+\infty}{+\infty}=\frac{6}{\sqrt{9}}=\frac{6}{3}=\bm{2}$

Бесконечная неопределенность между бесконечностью и показательными функциями

Наконец, нам осталось изучить только случай коэффициента неопределенности бесконечностей: насколько велика бесконечная неопределенность между бесконечностью и показательными функциями.

Рост показательной функции намного больше, чем рост полиномиальной функции, поэтому надо учитывать, что степень показательной функции больше, чем степень полиномиальной функции.

$\text{exponencial}>\text{polinomio}» title=»Rendered by QuickLaTeX.com» height=»16″ width=»192″ style=»vertical-align: -4px;»> Следовательно, если бесконечная неопределенность, разделенная на бесконечность, получается из предела с показательными функциями, то достаточно применить те же правила, объясненные для степеней числителя и знаменателя, но с учетом того, что показательная функция имеет более высокий порядок, чем многочлен. . Кроме того, если у нас есть показательные функции в числителе и знаменателе деления, показательная функция с большим основанием будет более высокого порядка. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

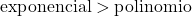
В этом случае знаменатель образован показательной функцией, поэтому он имеет более высокий порядок, чем числитель. Следовательно, неопределенная форма бесконечности между бесконечностью исчезает.

Решенные упражнения бесконечной неопределенности между бесконечностью

Упражнение 1

Вычислите предел следующей рациональной функции:

$\displaystyle\lim_{x \to +\infty} \cfrac{6x-5}{x^2-1}$

посмотреть решение

При вычислении предела мы получаем бесконечную неопределенность между бесконечностью, но так как степень числителя меньше степени знаменателя, то неопределенный предел равен нулю.

$\displaystyle \lim_{x \to +\infty} \cfrac{6x-5}{x^2-1} = \cfrac{6(+\infty)}{(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{0}$

Упражнение 2

Решите следующий неопределенный предел:

$\displaystyle\lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4}$

посмотреть решение

При попытке вычислить предел получается неопределенность ∞/∞. В этом случае степень полинома числителя больше степени полинома знаменателя, поэтому неопределенный предел равен плюс бесконечности.

$\displaystyle \lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4} = \cfrac{(+\infty)^3}{5(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{+\infty}$

Упражнение 3

Решите следующий предел на бесконечности:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

посмотреть решение

Предел дает неопределенность минус бесконечность между плюс бесконечность. Степень числителя больше степени знаменателя, поэтому неопределенный предел равен плюс бесконечности. Однако, поскольку при делении отрицательная бесконечность на положительную бесконечность, результат будет минус бесконечность.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Упражнение 4

Решите следующий неопределенный предел:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

посмотреть решение

В этой задаче бесконечная неопределенная форма на бесконечности получается из частного двух многочленов одной степени, поэтому результатом неопределенного предела является деление их главных коэффициентов:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Упражнение 5

Вычислите следующий предел хотя бы до бесконечности:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

посмотреть решение

Степень алгебраического выражения числителя меньше степени выражения знаменателя, поэтому неопределенность +∞/+∞ дает 0:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Упражнение 6

Решите следующий неопределенный предел функции с корнями:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

посмотреть решение

Выражение для числителя находится под радикалом, поэтому его степень равна 7/3. С другой стороны, многочлен в знаменателе квадратичен. А поскольку 7/3>2, то предел дает плюс бесконечность:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=+\infty$

Упражнение 7

Определите предел бесконечности следующей функции с дробями:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

посмотреть решение

В этом упражнении неопределенность минус бесконечность, разделенная на минус бесконечность, получается со степенью числителя, большей степени знаменателя, поэтому:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Упражнение 8

Найдите предел хотя бы до бесконечности следующей функции:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

посмотреть решение

Полином знаменателя является квадратичным, а полином числителя линейным. Следовательно, бесконечность неопределенности, разделенная на бесконечность, дает 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Упражнение 9

Решите хотя бы бесконечный предел следующей функции:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

посмотреть решение

Числитель имеет большую степень, чем знаменатель, поэтому результат неопределенной формы ∞/∞ будет бесконечным. Кроме того, знак бесконечности будет отрицательным, поскольку положительное, разделенное на отрицательное, дает отрицательное:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Упражнение 10

Решите следующий предел с бесконечной неопределенностью между бесконечностью:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

посмотреть решение

Показательная функция имеет более высокий порядок, чем полиномиальная функция, поэтому предел будет давать бесконечность. Однако, разделив положительное на отрицательное, знак бесконечности будет отрицательным:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Упражнение 11

Рассчитайте следующий предел:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2}$

посмотреть решение

В этой задаче неопределенность, бесконечная на бесконечности, решается путем деления доминирующих коэффициентов двух многочленов, поскольку они имеют одинаковую степень:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2} = \cfrac{(-\infty)^3}{-(-\infty)^3} = \cfrac{-\infty}{-(-\infty)}= \cfrac{-\infty}{+\infty}=\cfrac{1}{-1}=\bm{-1}$

Упражнение 12

Решите предел следующей функции, когда x приближается к бесконечности:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}$

посмотреть решение

Хотя неизвестное в числителе не возводится в квадрат непосредственно, при решении примечательного тождества мы ясно видим, что степень числителя больше степени знаменателя. Еще:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}=\lim_{x \to +\infty} \cfrac{x^2+9+6x}{x} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

Упражнение 13

Вычислите предел бесконечности следующей функции с кубическим корнем:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}$

посмотреть решение

Числитель состоит из кубического корня, поэтому его степень равна 3/3=1. Тогда степень числителя равна степени знаменателя, поэтому бесконечная неопределенность между бесконечностью разрешается следующим образом:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}= \cfrac{\sqrt[3]{8(+\infty)^3}}{-4(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt[3]{8}}{-4}=\cfrac{2}{-4}=\bm{-}\mathbf{\cfrac{1}{2}}$

Упражнение 14

Решите предел до бесконечности следующей функции с двумя радикалами:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

посмотреть решение

Степень числителя 7/3 = 2,33, степень знаменателя 5/2 = 2,5. Следовательно, поскольку степень числителя меньше степени знаменателя, неопределенный бесконечный предел между бесконечностью равен 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Упражнение 15

Рассчитайте следующий предел:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

посмотреть решение

Независимо от степени числителя, поскольку в знаменателе у нас показательная функция, результат неопределенной формы бесконечность над бесконечностью равен 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Как решить бесконечную неопределенность между бесконечными

степень числителя меньше степени знаменателя

Пример 1:

Пример 2:

степень числителя равна степени знаменателя

Пример 3:

Пример 4:

Степень числителя больше степени знаменателя

Пример 5:

Пример 6:

Бесконечная неопределенность между бесконечностью с корнями

Бесконечная неопределенность между бесконечностью и показательными функциями

Решенные упражнения бесконечной неопределенности между бесконечностью

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Упражнение 6

Упражнение 7

Упражнение 8

Упражнение 9

Упражнение 10

Упражнение 11

Упражнение 12

Упражнение 13

Упражнение 14

Упражнение 15

Оставьте комментарий Отменить ответ