Как вычислить модуль вектора

На этой странице вы увидите объяснение величины вектора и способов ее расчета по формуле. Вы также сможете увидеть, как найти модуль по двум точкам: его начало и конец. Кроме того, вы узнаете, как определять компоненты вектора по его модулю и свойствам модуля вектора. Вы даже можете попрактиковаться с примерами, упражнениями и пошаговыми задачами.

Что такое модуль вектора?

Величина вектора представляет собой расстояние между его началом и концом. Следовательно, величина вектора равна длине указанного вектора.

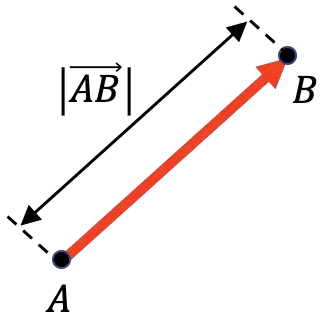
Как вы можете видеть на графическом представлении выше, величина вектора обозначается вертикальной полосой на каждой стороне вектора:

$\lvert \vv{AB}\rvert$

С другой стороны, модуль вектора совпадает с нормой вектора , поэтому вы также можете видеть, что он записан таким же образом. Вот почему есть математики, которые также представляют модуль вектора двумя вертикальными чертами с каждой стороны:

$\lvert \lvert \vv{AB}\rvert\rvert$

Формула модуля вектора

Чтобы найти величину вектора на плоскости, необходимо применить следующую формулу:

Чтобы определить величину вектора, мы должны вычислить (положительный) квадратный корень из суммы квадратов его составляющих. Другими словами, если у нас есть следующий вектор:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Его модуль:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

Например, мы рассчитаем величину следующего вектора по формуле:

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

Вычислить величину вектора по координатам его начала и конца.

Мы только что видели, как определяется величина вектора, когда мы знаем его компоненты, но что произошло бы, если бы мы знали только точки, где он начинается и где заканчивается?

Таким образом, чтобы вычислить величину вектора по координатам его начала и конца, необходимо выполнить следующие два шага:

Сначала находим компоненты вектора. Для этого нам нужно вычесть экстремум минус начало координат.
А затем вычисляем модуль полученного вектора по формуле, которую мы видели в предыдущем разделе.

Давайте посмотрим, как это делается, на примере:

Вычислить величину вектора, началом которого является точка
$A(2,1)$

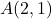
и в качестве финального пункта

$B(-1,4).$

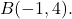
Сначала нам нужно найти компоненты вектора, поэтому мы вычитаем его конечную точку минус начало координат:

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

Зная вектор, мы вычисляем его величину, используя формулу векторной величины:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

А результат оставляем квадратным корнем, потому что он неточный.

Как вычислить компоненты вектора по его модулю

Мы видели, как извлечь величину вектора из его компонентов, но этот процесс также можно обратить вспять. Другими словами, мы можем вычислить компоненты вектора через его модуль.

Процесс нахождения компонентов вектора по его величине называется векторным разложением . Итак, чтобы разложить вектор, нам, очевидно, нужна его величина и угол, который он образует с осью абсцисс (ось X).

Так что компоненты вектора X и Y можно вычислить с помощью тригонометрических отношений:

Как вы можете видеть на изображении, величина вектора со своими компонентами образует прямоугольный треугольник, поэтому можно применить элементарные формулы тригонометрии.

Необходимо учитывать, что в отличие от модуля вектора его компоненты могут быть отрицательными, поскольку синус и косинус могут принимать отрицательные значения.

В качестве примера решим векторное разложение вектора, величина и угол которого с осью OX равны:

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

Горизонтальная составляющая вектора равна модулю, умноженному на косинус угла:

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

А вертикальная составляющая вектора равна умножению модуля на синус угла:

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

Итак, вектор следующий:

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

Модульные свойства вектора

Модуль — это тип векторной операции, который имеет следующие характеристики:

Величина вектора никогда не может быть отрицательной , она всегда будет равна или больше 0.

$\lvert \vv{\text{u}} \rvert \geq 0$

Фактически, единственный вектор, который существует с нулевой величиной, — это нулевой вектор, т.е. вектор

$\vv{\text{u}}= (0,0) .$

Величина произведения вектора на действительное число (или скаляр) эквивалентна умножению абсолютного значения скаляра на величину вектора. Следовательно, имеет место следующее равенство:

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

Треугольное неравенство проверено: модуль суммы двух векторов меньше или равен сумме их модулей по отдельности.

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

Кроме того, величина суммы двух векторов связана со скалярным произведением следующим уравнением:

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

единичный вектор

В математике единичным вектором называется вектор, модуль которого равен единице.

$\lvert \vv{\text{u}} \rvert=1$

Следовательно, длина единичного вектора равна одной единице.

Может показаться очень трудным, чтобы вектор имел модуль, равный ровно 1, но на самом деле найти этот тип вектора легко:

Чтобы найти единичный вектор любого вектора, просто разделите его на его модуль:

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

Золото

$\vv{\text{v}}_u$

— единичный вектор

$\vv{\text{v}},$

$\lvert \vv{\text{v}} \rvert$

ваш модуль.

Единичный вектор также называют версором или нормализованным вектором.

Кроме того, единичный вектор имеет то же направление и направление, что и исходный вектор.

Например, мы вычислим единичный вектор следующего вектора:

$\vv{\text{v}}=(1,-1)$

Чтобы нормализовать вектор, нам сначала нужно вычислить его величину:

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

И, наконец, вычисляем единичный вектор, разделив исходный вектор на его модуль:

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

Решенные упражнения векторного модуля

Упражнение 1

Вычислите величину следующего вектора:

$\vv{a}=(6,8)$

посмотреть решение

Чтобы вычислить модуль вектора, мы должны применить его формулу:

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

Упражнение 2

Упорядочите следующие векторы от самого короткого к самому длинному.

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

посмотреть решение

Длина вектора равна его величине. Следовательно, нам необходимо вычислить модули всех векторов:

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

Таким образом, векторы, упорядоченные от наименьшей до наибольшей длины (или модуля):

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

Упражнение 3

Определить величину вектора, началом которого является точка

$A(-3,2)$

и в качестве финального пункта

$B(7,-4).$

посмотреть решение

Чтобы вычислить его модуль, необходимо сначала найти вектор. Для этого вычитаем экстремум минус начало координат:

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

Как только мы знаем вектор, его модуль рассчитывается по формуле модуля:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

Упражнение 4

Разложим следующий вектор и найдем его компоненты:

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

посмотреть решение

Горизонтальная составляющая вектора равна модулю, умноженному на косинус угла:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

А вертикальная составляющая вектора равна умножению модуля на синус угла:

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

Итак, вектор следующий:

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

В данном случае две составляющие идентичны, то есть угол наклона вектора составляет 45°.

Упражнение 5

Вычислите вектор с тем же направлением и направлением, что и следующий вектор, но с модулем 1.

$\vv{a} = (-4,3)$

посмотреть решение

Вектор того же направления и того же направления, но с модулем 1, является единичным вектором. Чтобы его вычислить, сначала находим модуль вектора:

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$

А теперь вычисляем единичный вектор, разделив исходный вектор на его модуль:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(-4,3)}{5}= \bm{\left(-\frac{4}{5},\frac{3}{5} \right)}$

Упражнение 6

Векторно разложите следующий вектор и вычислите его единичный вектор:

$\lvert \vv{a} \rvert =6 \qquad \alpha = 20º$

посмотреть решение

Сначала разложим вектор и найдем его координаты:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(20º)= 6 \cdot 0,94 = 5,64$

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(20º)= 6 \cdot 0,34 = 2,05$

Итак, вектор следующий:

$\vv{a}= (5,64 \ ,\ 2,05)}$

А теперь вычислим единичный вектор, разделив полученный вектор на его модуль:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(5,64 \ ,\ 2,05)}{6}= \bm{(0,94 \ , \ 0,34) }$

Обратите внимание, что компоненты единичного вектора равны косинусу и синусу угла, который он образует с осью X.

Что такое модуль вектора?

Формула модуля вектора

Вычислить величину вектора по координатам его начала и конца.

Как вычислить компоненты вектора по его модулю

Модульные свойства вектора

единичный вектор

Решенные упражнения векторного модуля

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Упражнение 6

Оставьте комментарий Отменить ответ