Идентичность или матричная единица

На этой странице вы увидите, что такое матрица идентичности (или единицы), а также несколько примеров. Кроме того, мы объясняем, каковы свойства единичной матрицы, как работать с матрицей этого типа и каков результат ее определителя. Наконец, вы найдете приложения, которые имеет эта конкретная матрица.

Что такое единичная матрица?

Матрица идентичности (или единицы измерения) представляет собой квадратную матрицу, заполненную нулями (0), за исключением главной диагонали, где все элементы равны единицам (1).

Это определение единичной матрицы или единичной матрицы, но вы наверняка увидите это более четко на примерах:

Примеры единичных матриц

Пример единичной матрицы размерности 2 × 2

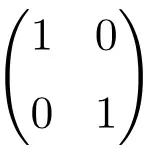
уникальный идентификатор или матрица размером 2x2

Пример Идентификационной матрицы порядка 3×3

единичная или уникальная матрица размером 3x3

Пример идентификационной матрицы размером 4×4

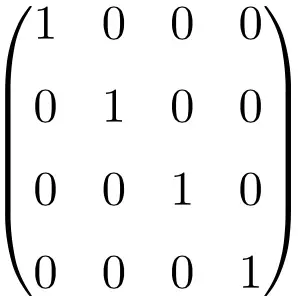
единичная или уникальная матрица размером 4x4

Как видите, для построения единичной матрицы нам все равно нужно проделать ту же процедуру: поставить на главной диагонали единицы (1), а остальные — нули (0). Единственное, что меняется, это размер таблицы.

Свойства таблицы идентификаторов

Единичная матрица, единичная матрица или даже тождественная матрица широко используются в математике, и это связано с характеристиками, которыми обладает этот тип матрицы:

Единичная матрица является примером диагональной матрицы .

Унитарная матрица — это одновременно верхняя и нижняя треугольная матрица .

Единичная матрица также является симметричной матрицей .

Заместителем идентификационной матрицы является она сама.

$\displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Это обратимая матрица. А что касается сопряженного, то обратная матрица Единицы сама по себе равна:

$\displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Любую скалярную матрицу можно получить умножением числа на единичную матрицу:

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

Все собственные значения (или собственные значения) Идентичной матрицы равны 1:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

Наконец, единичная матрица также является примером матрицы перестановок .

Операции с матрицей идентичности (или подразделения)

Вы, наверное, думаете: все это очень хорошо, но… а для чего нужна Матрица Личностей? Если бы это была таблица с 0 и 1!

Хотя вы, возможно, еще не затронули эту тему, единичная матрица часто используется в математике, на самом деле этот тип квадратной матрицы очень важен в линейной алгебре. Основная полезность единичной матрицы — это простота, с которой она позволяет производить вычисления матричных операций. Итак, давайте посмотрим, как работать с матрицей Identity:

Сложение и вычитание с помощью матрицы идентичности

Один из способов сложения (или вычитания) чисел на главной диагонали матрицы без изменения других элементов — использовать единичную матрицу, поскольку она добавляет (или вычитает) к этим числам только одну единицу. элементы:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

Вы также можете добавить или вычесть дополнительные единицы к элементам на диагонали, сначала умножив единичную матрицу на скаляр:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

Умножение матрицы на единичную матрицу

При умножении матрицы на единичную матрицу она действует как нейтральный элемент , то есть любая матрица, умноженная на единичную матрицу, дает ту же матрицу. Взгляните на следующий пример:

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Более того, смысл произведения матрицы не имеет значения, или, другими словами, не имеет значения, умножаем ли мы единичную матрицу справа или слева, потому что результатом всегда будет одна и та же матрица. Чтобы продемонстрировать это, мы повторяем предыдущее упражнение, но на этот раз умножая матрицу идентичности на противоположную сторону:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Мощность единичной матрицы

Степень единичной матрицы всегда приводит к единичной матрице, независимо от показателя степени, до которого мы возводим матрицу, и ее размерности.

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Определитель единичной матрицы

Как я полагаю, вы уже догадались, определитель матрицы Идентичности (или Единицы) всегда равен 1 , независимо от размерности матрицы.

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

Приложения матрицы идентичности

Наконец, после всей этой информации вы, вероятно, уже знаете, как ответить на типичный вопрос: почему так важна идентификационная матрица? Расслабься, я тоже задавал себе этот вопрос раньше. 😂

Как вы заметили, идентификационная матрица имеет множество применений и именно поэтому она так интересна. Одним из применений матрицы Unit являются операции, поскольку, как мы видели, с ней очень легко выполнять матричные операции.

С другой стороны, единичная матрица также используется для решения матричных уравнений . Для этого воспользуемся следующим свойством обратной матрицы: умножение матрицы на ее обратную матрицу равно единичной матрице. Посмотреть, как решить уравнение с матрицами, можно, перейдя по ссылке.

Кроме того, единичная матрица также используется для расчета обратной матрицы методом Гаусса. Этот метод предполагает размещение матрицы рядом с единичной матрицей, образуя таким образом матрицу большего размера. Затем исходную матрицу необходимо преобразовать в единичную, применяя к строкам элементарные операции. Это кажется очень сложным, но на самом деле это не так уж и много, однако необходимо применить целую процедуру, поэтому, если вас больше интересует, вы можете поискать, как инвертировать матрицу, в поисковой системе веб-страницы (сверху СПРАВА).

Наконец, матрица идентичности также полезна для диагонализации матрицы и вычисления ее собственных значений (или собственных значений). Потому что с помощью определенных операций, в которые вмешивается единичная матрица, можно получить характеристический полином, из которого получаются собственные значения. Но это уже очень сложная тема, поэтому у нас есть целая суперподробная страница, посвященная диагонализации матриц с примерами и решенными упражнениями, объясняющими ее. Если вас это больше интересует, вы можете найти это руководство в нашей поисковой системе (вверху справа).