Математическая запись — это способ передачи идей и вычислений с помощью символов. Хотя на первый взгляд это может показаться запутанным, после небольшой практики вы сможете легко это интерпретировать. В этой статье мы покажем вам значение всех символов, используемых в этих обозначениях, и несколько примеров их применения.
Что такое математическая запись?
Математическая запись — это способ записи значений и выражений, используемый в математике. Этот метод позволяет математикам кратко и точно излагать идеи. Математическая запись также позволяет тем, кто занимается или изучает математику, лучше понимать концепции.
Язык математики не следует путать с научной нотацией, которая представляет собой способ записи числовых значений. Между тем математическая нотация — это скорее набор символов , позволяющих писать сложные выражения, как в языке. Мы вернемся к этой теме более подробно позже.
Как читать математические обозначения?
Научиться интерпретировать математические обозначения проще, чем кажется, вам просто нужно выучить значение каждого символа, и как только вы это сделаете, вы сможете читать все, что написано в математических обозначениях. Это так просто, хотя, очевидно, требует практики и много времени на обучение.
Математические выражения очень логичны и всегда следуют закономерностям, поэтому вам просто нужно запомнить правила, и тогда вы сможете экстраполировать их на любую ситуацию. Мы можем даже описывать очень сложные вычисления, в этом заключается магия математического языка, который позволяет методично передавать очень сложные сообщения.
Компоненты математической записи
Математическая запись состоит из ряда символов , обозначающих числа, операции и отношения между ними. На первый взгляд эти символы могут показаться сложными, но, приложив немного практики и понимания, интерпретация математических обозначений станет детской игрой.
Далее мы подробно объясним четыре типа элементов, которые можно встретить на математическом языке. Начиная с самого простого и заканчивая самым сложным и абстрактным. И как только теоретическое объяснение будет закончено, мы поговорим о существующих типах числовых обозначений .
Числа и наборы чисел
Прежде всего, мы должны дать определение математическим числам , это математическое понятие, обозначающее величину, относящуюся к единице. Мы можем описать любое числовое значение, следуя десятичной системе счисления и комбинируя следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
Если мы упорядочим числа по разным свойствам, мы получим несколько категорий чисел, называемых наборами чисел. И эти группы значений также имеют свои обозначающие их символы , в следующем списке мы представляем их все с названием соответствующей группы:
- ℙ: простые числа
- ℕ: натуральные числа
- ℤ: Целый
- ℚ: рациональные числа
- ℝ: Действительные числа
- 𝕀: мнимые числа
- ℂ: комплексные числа
- ℍ: Кватернионы
Эти символы обычно используются в наших расчетах для одновременного определения широкого диапазона чисел. Например, если у нас есть выражение, которое принимает множество значений соответственно, то вместо того, чтобы писать числа по одному, нам будет проще указать эти значения через символ, соответствующий их числовой группе .
Операторы и квантификаторы
Теперь, когда мы обсудили числа, составляющие суть математики, нам нужно поговорить об операторах и кванторах . Первые — это все те символы, которые позволяют нам представлять операции: сложение (+), вычитание (-), умножение (x или ·), деление (÷) и другие.
Однако у нас также есть два других типа операторов: логические операторы и операторы отношения. Первый выражает соединение, дизъюнкция и отрицание. Они помогают нам предлагать логические операции , которые, в отличие от арифметических операций, работают не с числами, а с математическими предложениями.
В то время как второй позволяет нам устанавливать эквивалентности и отношения между значениями или математическими выражениями. Эти символы можно использовать в арифметических вычислениях (для упорядочивания чисел), но они более важны в алгебре, когда у нас есть переменные (подробнее об этом в двух разделах).
В следующем списке вы можете найти определения всех операторов, которые мы обсуждали до сих пор:
| Символ | Определение | Добрый |
| + | Добавление | арифметический оператор |
| – | Вычитание | арифметический оператор |
| ИКС, *, · | Умножение | арифметический оператор |
| ÷ | Разделение | арифметический оператор |
| х² | расширение прав и возможностей | арифметический оператор |
| √ | депозит | арифметический оператор |
| И | Соединение | логический оператор |
| ИЛИ | Дизъюнкция | логический оператор |
| НЕТ | Отрицание | логический оператор |
| «=» | Равно | оператор отношения |
| > | Больше чем | оператор отношения |
| < | Меньше чем | оператор отношения |
| >= | Лучше или равно | оператор отношения |
| <= | меньше или равно | оператор отношения |
| ≠ | не равен | оператор отношения |
| ≡ | Точно так же | оператор отношения |
| ≈ | почти равный | оператор отношения |
| ≃ | Эквивалентно | оператор отношения |
| ∝ | Пропорциональный | оператор отношения |
Хотя есть еще пять логических операторов, которые используются для объяснения математической логики из теории множеств. Это ветвь, которая применяет логику множеств , которая используется в расчетах, геометрии, статистике… Затем мы покажем вам используемые символы и их определение.
| Символ | Определение |
| х € А | x принадлежит A |
| х ∉ А | x не принадлежит A |
| ∪ | союз |
| ∩ | Пересечение |
| ⊂ | Включение |
Что касается кванторов, то их можно определить как символы, обозначающие количество элементов множества, удовлетворяющих определенному условию (эквивалентность, порядок, принадлежность и т. д.). Существует большое разнообразие операторов, но среди наиболее используемых можно выделить:
| Символ | Определение | Добрый |
| ∀x | для всех х | количественно оценить |
| ∃x | Существует хотя бы один х | количественно оценить |
| ∄x | нет х | количественно оценить |
| ∃!x | Есть только один х | количественно оценить |
| | | Такой как | количественно оценить |
| ∴ | ТАК | количественно оценить |
Математические выражения и их отношения
С помощью символов, которые мы рассмотрели до сих пор, вы можете понять многие математические задачи, но мы еще не объяснили их применение или взаимосвязь в сложных выражениях, таких как комбинированные операции или алгебраические вычисления. Плюс, есть еще символы отношений, которые стоит обсудить. Именно их мы увидим в этом разделе.
Начиная с символов группировки, это круглые, квадратные и фигурные скобки. Эти элементы необходимы при обозначении сложных формул. Его основная функция — отдать приоритет определенным вычислениям в глобальном выражении. И среди трех типов существуют разные уровни приоритета. В этом выражении вы можете увидеть порядок записи 3 {[2 + (3 – 2) · 2] – 4}.
| символы | Определение | Приоритет |
| «(«И»)» | Круглые скобки | Максимальный приоритет |
| «[«И»]» | Кронштейны | второй приоритет |
| «{» И «}» | Ключи | третий приоритет |
И чтобы закончить эту категорию, мы поговорим о суммах (Σ) и произведениях (∏) , которые являются элементами, позволяющими нам описывать повторяющиеся сложения и умножения. Суммирование эквивалентно высказыванию: «сумма Xi, где i принимает значения от 1 до an». И произведение то же самое, но вместо сложения мы умножаем.
алгебраический анализ
Первое, что следует обсудить применительно к алгебраическим символам, — это переменные, которые представлены буквами алфавита. Их функция — имитировать число , но они не имеют фиксированного значения, как математические константы , поэтому могут принимать новые значения. Это относится к уравнениям, пределам, производным, интегралам, матрицам…
Наконец, мы хотим поговорить о представлениях всех этих алгебраических операций , о которых мы только что говорили в последнем абзаце. С тех пор они являются основой алгебры и вам необходимо знать, какова их символика. Далее мы покажем вам таблицу с различными символами и кратким определением:
| Символ | Определение |
| лим х → б | Предел (когда x стремится к b) |
| y’, ƒ’ (x), dy / dx | производная |
| ∫ | Полный |
| В МХН | Матрица размеров mxn |
Вывод о символах математического языка
Пока вы рассмотрели все важные символы, рассматриваемые в математике, очевидно, есть еще что обсудить. Но они более специфичны для каждой подкатегории математики: геометрии, статистики, алгебры… Поэтому мы закроем эту тему и поговорим о числовых обозначениях.
Виды числовых обозначений
В этом разделе мы увидим все способы выражения математических чисел, поскольку для этого существуют разные обозначения. Вначале мы упомянули десятичную систему счисления, которая наиболее часто используется математиками. Далее мы объясним это более подробно и покажем вам другие типы математических обозначений:
десятичная система счисления
Десятичная система счисления — это позиционная система счисления (система, в которой положение каждой цифры будет определять ее значение), основанная на кратных и дольных числах числа 10. Поскольку десять — это число, используемое в качестве числовой основы . Следовательно, мы будем использовать десять числовых символов: 1, 2, 3, 4, 5, 6, 7, 8, 9 и 0.
Значение этих чисел определяется из суммы цифр, умноженной на степени по основанию десять, установленные согласно положению . И очень важно помнить, что для записи числа меньше единицы необходимо использовать десятичную точку. Ниже приведен пример:
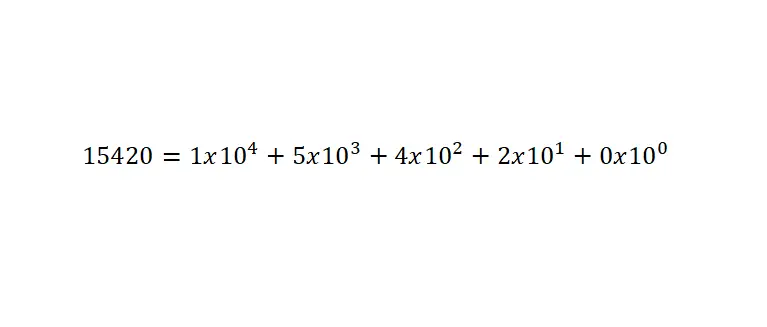
Научная нотация
Экспоненциальная форма записи или научная запись, несомненно, является одним из наиболее часто используемых типов записи в науке и технике. Действительно, это позволяет нам простым способом выражать очень большие и очень маленькие числа. Чтобы понять определение научной записи, мы объясним, как передать целое число в эту запись:
- Перемещение десятичной точки: вы должны переместить десятичную точку столько раз, сколько необходимо, пока не дойдете до первой цифры (влево, если у вас очень большое число, и вправо, если у вас очень маленькое число).
- Установите основу: напишите это последнее число, умноженное на десять, так, рядом со значением, которое вы получили, отведя десятичную запятую в одну сторону, необходимо написать умножение на десять: «х 10».
- Добавьте показатель степени: со значением, равным количеству раз, когда вы переместили десятичную точку. Для больших чисел вы оставите показатель степени положительным, а для маленьких вы должны записать его с отрицательным знаком.
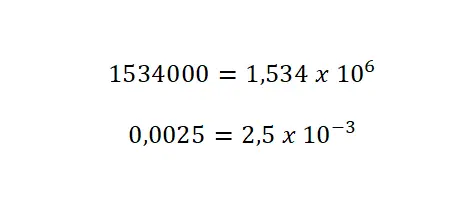
шестнадцатеричная запись
Шестнадцатеричная система основана на числе 16, что означает, что она использует шестнадцать различных символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Как вы можете видите, эта система счисления состоит из цифр десятичной системы и шести букв. Это обозначение обычно используется, в частности, в ИТ и во всем, что с ним связано.
Важно уточнить, что, поскольку оно имеет общие с другими видами записи символы, мы всегда должны указывать, что оно записано в шестнадцатеричном виде, с помощью скобки и индекса 16 . В следующем примере на очень наглядном примере вы можете увидеть преобразование шестнадцатеричного числа в десятичную систему счисления:
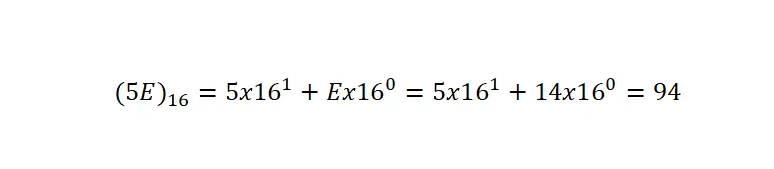
Чтобы преобразовать шестнадцатеричное число в десятичное выражение, нам нужно разбить число на его основные умножения, как мы это делали в десятичной записи, но изменив основание на 16 . Далее мы умножим каждую цифру на шестнадцать, возведя ее в положение, в котором эта конкретная цифра занимает минус единица.
восьмеричная запись
Последняя система, о которой мы поговорим, — это восьмеричная система счисления , которая имеет основание 8. Это означает, что она использует только восемь символов или цифр: 0, 1, 2, 3, 4, 5, 6 и 7. Эта система используется реже всего. система нумерации всех тех, которые мы объяснили. Следует отметить, что преобразования этой записи производятся по той же процедуре, что и предыдущие.
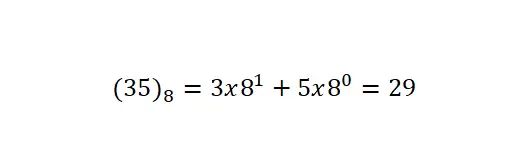
новые обозначения
Наконец, можно говорить о римской системе счисления , которая сегодня не получила широкого распространения, но в прошлом имела очень важное значение в области математики. Поскольку это была одна из нотаций, которая оживила математику.
Ваше написание ограничено 7 символами: I (1), V (5), X (10), L (50), C (100), D (500) и M (1000). И соединив эти буквы, пишутся все цифры. Если вы хотите знать , как они объединяются , образуя другие, более крупные числа, рекомендуем прочитать о них нашу статью, доступную по последней ссылке.
Как улучшить производительность чтения в математической записи?
Есть несколько способов улучшить производительность при чтении математических обозначений. Один из способов — прочитать символы и цифры вслух. Другой способ – ознакомиться с символами и их значением. Вы также можете попрактиковаться в чтении математических обозначений, используя упражнения и задачи.
Мы надеемся, что помогли вам с этим руководством, пожалуйста, если у вас есть какие-либо вопросы, не стесняйтесь писать их в комментариях . Или, если вы хотите внести свой вклад по этой теме, мы надеемся увидеть это и в комментариях. Тем не менее, мы оставляем вам статью о том, как изучать математику , на случай, если вы захотите продолжить чтение.