Линейная регрессия — это статистический метод , используемый для изучения взаимосвязи между двумя непрерывными переменными . Основная идея линейной регрессии — найти прямую линию, которая лучше всего соответствует данным. Кроме того, он позволяет прогнозировать значение одной переменной на основе значения другой.
Эта прямая линия называется «регрессией» и используется для прогнозирования неизвестных значений или для понимания взаимосвязи между переменными. Таким образом, линейная регрессия — это инструмент для анализа и моделирования взаимосвязей между двумя непрерывными переменными.
Почему линейная регрессия важна?
Линейная регрессия важна, поскольку позволяет моделировать и анализировать взаимосвязь между двумя непрерывными переменными , что может быть полезно для прогнозирования будущих значений и выявления закономерностей и тенденций в данных.
Кроме того, линейная регрессия является фундаментальным инструментом в статистике и большинстве областей научных и социальных исследований, включая экономику, психологию, медицину, инженерное дело и физику, среди других. Он также используется при принятии бизнес-решений и оптимизации процессов в промышленности и бизнесе.
Таким образом, линейная регрессия — это мощный и универсальный инструмент, который позволяет анализировать и лучше понимать данные и взаимосвязи между переменными в различных областях исследований и практики.
Каковы типы линейной регрессии?
Существует несколько типов линейной регрессии, некоторые из них:
простая линейная регрессия
Простой линейный регрессионный анализ — широко используемый инструмент для изучения влияния независимой переменной на одну зависимую переменную , при котором считается, что между ними существует линейная связь. Простое уравнение линейной регрессии позволяет оценить значения зависимой переменной на основе значений независимой переменной.
Простая формула линейной регрессии:
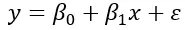
Где β 0 — значение зависимой переменной, когда независимая переменная равна нулю. β 1 представляет собой изменение зависимой переменной на единицу изменения независимой переменной, а ε представляет собой невязку или ошибку. То есть изменчивость данных, которую нельзя объяснить линейной зависимостью формулы.
Множественная линейная регрессия
Множественная линейная регрессия используется, когда существует более одной независимой переменной, которая может повлиять на изучаемую зависимую переменную .
Формула множественной линейной регрессии:
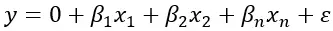
Где Y представляет собой зависимую переменную , β 1 , β 2 , β n — независимые переменные, которые могут повлиять на значение Y, регрессию, а ε представляет собой возможную существующую ошибку. Эта формула позволяет нам оценить значение Y на основе значений независимых переменных.
Какова формула линейной регрессии?
Формула линейной регрессии:
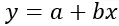
Золото:
y — зависимая переменная (или реакция), которую необходимо спрогнозировать.
x — независимая переменная (или предиктор), используемая для прогнозирования.
a — точка пересечения (или точка, в которой линия регрессии пересекает ось Y, когда x=0)
b — наклон линии регрессии (указывающий скорость изменения y для каждого изменения x)
Чтобы найти значения a и b, мы используем метод наименьших квадратов , который стремится минимизировать сумму квадратов ошибок между наблюдаемыми значениями и значениями, предсказанными линией регрессии.
Вот формулы:
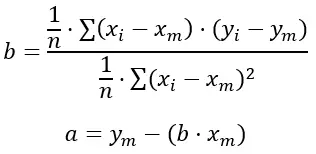
Золото:
n — общее количество имеющихся у нас наборов данных.
x i и y i — значения, которые мы принимаем при суммировании.
x m и y m — средние значения каждой переменной.
Как применить метод линейной регрессии?
Метод линейной регрессии можно применить, выполнив следующие шаги:
- Сбор данных . Первое, что нужно сделать, — это собрать данные , которые вас интересуют. Например, если вы хотите изучить взаимосвязь между зарплатой и возрастом группы людей, вам необходимо собрать информацию о зарплате и возрасте каждого из них.
- Постройте данные . Далее вам необходимо отобразить данные на декартовой плоскости, где независимая переменная (в данном случае возраст) расположена на горизонтальной оси, а зависимая переменная (зарплата) — на вертикальной оси.
- Определите линию регрессии . Необходимо определить линию регрессии, которая лучше всего соответствует данным. Эта линия получается по формуле линейной регрессии, которая рассчитывается с использованием выборочных статистических данных.
- Оцените степень соответствия . Важно оценить, насколько хорошо линия регрессии соответствует данным. Это можно сделать с помощью статистических измерений.
- Делайте прогнозы . Наконец, прогнозы можно делать, используя полученную линию регрессии. Например, если вы хотите спрогнозировать зарплату 30-летнего человека, вы должны использовать формулу линейной регрессии и подставить в нее значение возраста.
Важно отметить, что эти шаги могут незначительно отличаться в зависимости от типа используемой линейной регрессии и используемого статистического программного обеспечения.
Для чего используется линейная регрессия?
Линейная регрессия используется, когда вы хотите проанализировать взаимосвязь между двумя переменными , когда одна переменная может влиять на значение другой переменной. Таким образом, линейную регрессию можно использовать, чтобы понять, как независимая переменная влияет на зависимую переменную, и спрогнозировать значение зависимой переменной на основе независимой переменной.
Важно отметить, что линейная регрессия предполагает, что связь между двумя переменными линейна , а это означает, что изменение зависимой переменной пропорционально изменению независимой переменной.
Следовательно, линейную регрессию следует использовать, когда есть подозрение на линейную связь между двумя переменными. Если это условие не соблюдается, возможно, целесообразнее использовать другие модели нелинейной регрессии или другие статистические методы.
Каковы применения линейной регрессии?
Линейная регрессия используется в самых разных областях, таких как статистика, экономика, инженерия, социальные науки, биология и других. Вот некоторые из наиболее распространенных применений линейной регрессии:
- Анализ тенденций – для анализа тенденций в исторических данных и прогнозирования будущих тенденций.
- Прогнозирование – предсказание будущего значения переменной на основе прошлых значений одной или нескольких переменных.
- Исследование рынка : изучение взаимосвязи между спросом на товар и его ценой.
- Финансовый анализ – изучение взаимосвязи между доходами и расходами компании и прогнозирование будущих финансовых результатов.
- Эпидемиологические исследования : изучают связь между воздействием фактора риска и вероятностью развития заболевания.
- Социальные науки – изучение взаимосвязей между двумя или более переменными в таких областях, как психология, социология и политология.
- Исследование операций . Линейная регрессия используется для моделирования и оптимизации сложных систем в таких областях, как промышленное проектирование и логистика.
- Науки об окружающей среде – используются для изучения взаимосвязи между факторами окружающей среды и воздействием на экосистемы.
Что такое остатки в линейной регрессии?
Остатки в линейной регрессии представляют собой разницу между наблюдаемыми значениями зависимой переменной и значениями, предсказанными моделью линейной регрессии . Другими словами, это вертикальное расстояние между фактическими точками данных и линией регрессии.
Идея остатков заключается в том, что если линия регрессии хорошо соответствует данным, остатки должны быть небольшими и случайными. Если остатки велики или следуют определенному шаблону, это может быть признаком того, что связь между переменными не является линейной или что модель линейной регрессии не соответствует данным.
Остатки также используются для оценки точности модели линейной регрессии и выявления выбросов или влиятельных точек данных, которые могут повлиять на качество модели.
Могу ли я запустить линейную регрессию с более чем одной зависимой переменной?
В линейной регрессии зависимая переменная всегда представляет собой одну переменную. Однако у вас может быть более одной независимой переменной. В этом случае мы бы говорили о множественной линейной регрессии .
Цель множественной линейной регрессии — изучить влияние нескольких независимых переменных на одну зависимую переменную.
Как я могу интерпретировать коэффициенты линейной регрессии?
В линейной регрессии коэффициенты представляют собой наклон и точку пересечения линии регрессии . Наклон указывает изменение зависимой переменной на единицу изменения независимой переменной, а точка пересечения представляет значение зависимой переменной, когда независимая переменная равна нулю.
Численные примеры линейной регрессии
Простым примером может быть следующее:
Предположим, у нас есть следующие данные о возрасте и росте для группы людей:
| возраст) | Высота (см) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| Четыре пять | 190 |
Мы хотим определить, существует ли связь между возрастом и ростом этих людей. Для этого мы будем использовать линейную регрессию.
Сначала мы можем построить статистический график с данными (в этом случае мы рекомендуем использовать диаграмму рассеяния):
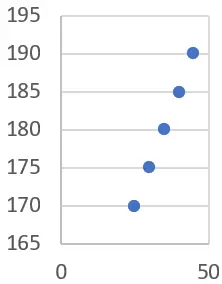
Мы видим, что существует четкая тенденция: с увеличением возраста рост также увеличивается. Мы можем подтвердить это, рассчитав линию линейной регрессии.
Рассчитав коэффициенты линии линейной регрессии по формулам, которые мы видели ранее, получаем:
при = 145
б = 1
Следовательно, уравнение линии линейной регрессии имеет вид:
Рост = 145 + 1 Возраст
Мы можем использовать это уравнение, чтобы предсказать рост человека в зависимости от его возраста. Например, если человеку 32 года, мы можем предсказать, что его рост будет:
Рост = 145 + 1 32 = 177 см.