На этой странице вы найдете определение конических сечений, почему они так важны, а также различные существующие типы конических сечений (круг, эллипс, гипербола и парабола). Кроме того, вы сможете увидеть различия между их уравнениями.
Что такое конические сечения?
В аналитической геометрии конические сечения (или просто коники) — это все кривые, возникающие в результате различных пересечений конуса и плоскости, когда эта плоскость не проходит через вершину конуса. Существует четыре типа конических сечений: круг, эллипс, парабола и гипербола.
Ниже приведены 4 возможных сечения, которые можно получить из любого конуса:
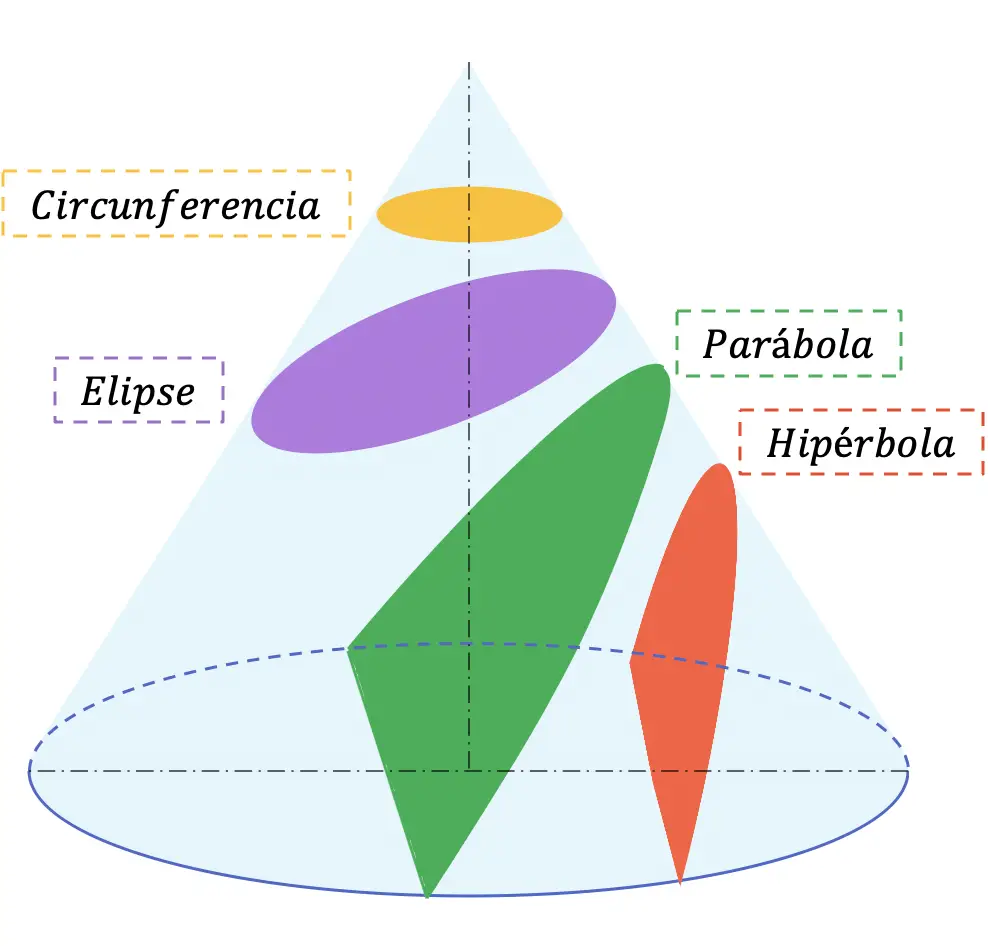
Конические сечения обычно изучаются в средней школе (Bachillerato) по предметам математики и черчения.
Виды конических сечений
Разобравшись с понятием конического сечения, давайте посмотрим, какие четыре типа конических сечений существуют: круг, эллипс, парабола и гипербола.
длина окружности
Окружность — это коническое сечение, которое можно найти, разрезав конус плоскостью, перпендикулярной его оси вращения (параллельной основанию).

Кроме того, окружность — это геометрическое место точек на плоскости, равноудаленных от фиксированной точки, называемой центром.
Эллипс
Эллипс представляет собой плоскую замкнутую изогнутую линию, очень похожую на окружность, но по форме более овальную. В частности, он возникает в результате рассечения поверхности конуса наклонной плоскостью, угол которой относительно оси вращения больше угла образующей.
Кроме того, все точки эллипса удовлетворяют условию: эллипс является геометрическим местом всех точек плоскости, сумма расстояний которых до двух других неподвижных точек (называемых фокусами F и F’) постоянна.

Притча
В математике парабола — это геометрическое место точек на плоскости, которые равноудалены от фиксированной точки (называемой фокусом) и фиксированной линии (называемой директрисой).

Геометрически парабола представляет собой результат сечения конуса плоскостью с углом наклона относительно оси вращения, эквивалентным углу образующей конуса. Следовательно, плоскость, содержащая параболу, параллельна образующей конуса.
Очень важной характеристикой этого конического сечения является уравнение параболы , поскольку в зависимости от своего состояния оно позволяет определить, к какому типу относится парабола. По этой ссылке вы найдете все уравнения параболы, каковы элементы параболы, их свойства, примеры, решенные упражнения… среди других характеристик парабол.
Гипербола
В качестве конического сечения гипербола получается, когда конус рассечен плоскостью с углом меньшим, чем угол, образуемый образующей конуса относительно его оси вращения.
Математически гиперболу можно определить как геометрическое место точек на плоскости, которые удовлетворяют следующему свойству: абсолютное значение разницы расстояний между любой точкой гиперболы и двумя неподвижными точками (называемыми фокусами) должно быть постоянным.
Более того, значение вычитания этих двух расстояний всегда эквивалентно расстоянию между двумя вершинами гиперболы.
![]()

Как я уверен, вы уже поняли, значение параметра
![]()
гиперболы является фундаментальным для гипербол. По следующей ссылке вы можете увидеть наше объяснение гиперболы, где вы узнаете, почему это такой важный коэффициент, а также какие элементы характеризуют гиперболу. Кроме того, вы узнаете, как выглядит уравнение гиперболы , какие существуют типы гипербол и даже пошаговые задачи и упражнения с гиперболами.
Общее уравнение конических сечений
Каждое коническое сечение можно аналитически выразить в виде уравнения. Фактически все конические уравнения должны быть второй степени:
![]()
Следовательно, хотя бы один из коэффициентов
![]()
или
![]()
формулы должно быть отличным от нуля.
Таким образом, в зависимости от значений параметров уравнение будет соответствовать тому или иному типу коники:
- Окружность : для общего уравнения, описывающего длину окружности, члены

И

должно совпадать и

должно быть равно нулю.
![]()
- Эллипс : уравнение будет соответствовать математическому выражению эллипса, если будет проверено следующее условие:
![]()
- Парабола : Чтобы уравнение было параболой, должно выполняться следующее равенство:
![]()
- Гипербола : Наконец, общее уравнение гиперболы должно удовлетворять следующему неравенству:
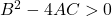 Навигация по записям
Навигация по записям