▷ Композиция функций (или составная функция)

В этой статье мы объясним, что такое составная функция (или композиция функций). Кроме того, вы сможете увидеть несколько примеров составных функций и способы вычисления области определения функций этого типа. Наконец, вы найдете свойства композиции функций и несколько пошаговых упражнений для практики.

Что такое композиция функций?

Композиция функций состоит из последовательного вычисления одного и того же значения независимой переменной (x) в двух или более функциях. Например, составление функций (gof)(x) дает составную функцию g[f(x)].

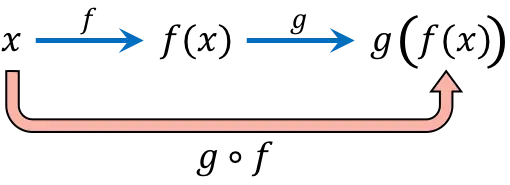
Выражение сложной функции

$g\circ f$

мы читаем «f, составленное из g» или «f, за которым следует g».

Обратите внимание, что порядок важен при композиции функций: сначала применяется функция справа от символа композиции.

$(f)$

тогда функция слева от символа композиции

$(g).$

Пример композиции функций

Учитывая определение составной функции, давайте посмотрим пример того, как вычислить композицию двух функций.

Учитывая следующие две разные функции:

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

Вычислить составную функцию

$\left(g \circ f\right)(x)$

и оценить его в

$x=3.$

Состав функций

$\left(g \circ f\right)(x)$

Это означает, что нам нужно выполнить следующую составную функцию:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Для ее решения заменим

$f(x)$

по его алгебраическому выражению:

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

И теперь мы берем функцию

$g(x)=\cfrac{x+4}{2}$

и мы помещаем выражение

$3x+1$

где есть один

$x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

Таким образом мы уже вычислили функцию f , состоящую из g :

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

Наконец, чтобы вычислить составную функцию в

$x=3$

Просто вычислите образ функции в указанном значении:

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

Область составной функции

Обычно, когда мы выполняем операции над функциями, область определения результирующей функции является пересечением областей определения исходных функций. Однако это свойство не удовлетворяется композицией функций.

Область композиции функций

$(g\circ f)(x)$

эквивалентно множеству всех значений x в области определения функции

$f$

такой как

$f(x)$

принадлежит области функции

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Следовательно, чтобы вычислить область определения составной функции, необходимо сначала найти область определения каждой функции отдельно, а затем область определения функции, полученной в результате операции. Таким образом, область композиции функций будет состоять из всех значений, удовлетворяющих предыдущему математическому условию.

👉 Помните, если вы столкнулись с проблемой, которую не знаете, как решить, вы можете задать ее нам в комментариях ниже!

Свойства композиции функций

Составные функции имеют следующие характеристики:

Композиция функций обладает свойством ассоциативности, поэтому всегда справедливо уравнение:

$f\circ (g\circ h)=(f\circ g)\circ h$

В общем случае композиция функций не является коммутативной, поэтому порядок операции определяет результат:

$f\circ g\neq g\circ f$

Нейтральный элемент состава функций соответствует тождественной функции
$f(x)=x.$

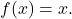
Таким образом, любая функция, составленная с помощью функции тождества, приводит к самой функции:

$f\circ id = id \circ f = f$

$id = x$

Вычисление обратной композиции двух функций эквивалентно сначала нахождению обратной каждой функции, а затем определению составной функции:

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Обратная функция также выступает симметричным элементом составной функции, поскольку композиция функции с обратной ей эквивалентна тождественной функции:

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

Производная композиции двух функций вычисляется по цепному правилу:

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤ Смотрите: какое правило цепочки?

Решенные упражнения на состав функций

Упражнение 1

Учитывая следующие две функции:

$f(x)=x-2 \qquad g(x)= 5x + 4$

Вычислите композиции функций f , составленных из g , и g, составленных из f .

$(g\circ f)(x)$

$(f\circ g)(x)$

Посмотреть решение

Состав функций

$\left(g \circ f\right)(x)$

означает вычисление следующей сложной функции:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Итак, чтобы решить эту проблему, мы заменяем

$f(x)$

для его выражения:

$f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

$g\Big(x-2\Big)$

Это означает, что в выражении

$g(x) =5x+4$

вам нужно заменить переменную

$x$

Для

$x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

Еще:

$\bm{\left(g \circ f\right)(x) = 5x-6}$

С другой стороны, чтобы найти функцию g , состоящую из f , вы должны проделать ту же процедуру, но в обратном порядке:

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

Это упражнение также демонстрирует то свойство, что составные функции не являются коммутативными, поскольку результат зависит от порядка применения функций.

Упражнение 2

Учитывая следующие две функции:

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

Вычисляет композицию функций f , составленных из g .

$(g\circ f)(x)$

Посмотреть решение

Функция f, составленная из g , означает решение следующей составной функции:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Поэтому мы заменяем функцию f(x) ее выражением:

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

И теперь нам предстоит заменить

$x$

Для

$x^2-3$

в выражении функции g(x):

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

Короче говоря, результат композиции функций:

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

Упражнение 3

Учитывая следующие две квадратичные функции:

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

Определим результат следующей композиции функций:

$(g\circ f)(2)$

Посмотреть решение

$\left(g \circ f\right)(2)$

состоит из нахождения следующей сложной функции:

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

Итак, чтобы решить составную функцию, мы сначала вычисляем

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

Поэтому, как

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

Итак, чтобы найти значение составной функции, вам просто нужно вычислить

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

Вкратце, результат задачи композиции функций таков:

$\bm{\left(g \circ f\right)(2) =8}$

Упражнение 4

Учитывая следующие две функции:

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

Найдите результат g , составленный с f в точке x=2:

$(f\circ g)(2)$

Посмотреть решение

В этом случае нам необходимо вычислить следующую составную функцию:

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

Итак, сначала мы находим

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

И так, как

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

Итак, чтобы решить сложную функцию, нам нужно вычислить

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$