Комплексная, сопряженная и транспонированная матрица

На этой странице вы увидите, что такое комплексные матрицы, сопряженные матрицы и сопряженные транспонированные матрицы. Теперь они очень похожи на вас, но вы увидите, что к концу страницы вы полностью поймете разницу между ними. Дополнительно мы увидим примеры каждого типа и его свойств.

комплексная матрица

Прежде чем перейти к объяснению сопряженной матрицы и транспонирования сопряженной матрицы, давайте рассмотрим концепцию комплексной матрицы:

Что такое комплексная матрица?

Комплексная матрица — это матрица, среди элементов которой имеется определенное комплексное число.

Напомним, что комплексное или мнимое число – это число, состоящее из действительной и мнимой частей, которое обозначается буквой i. Например:

$3+5i$

Примеры комплексных матриц

Давайте рассмотрим несколько примеров сложных многомерных массивов:

Пример комплексной матрицы порядка 2 × 2

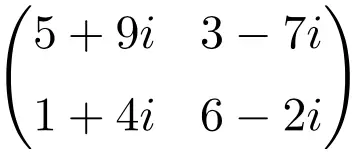
Пример комплексной матрицы размерности 3х3

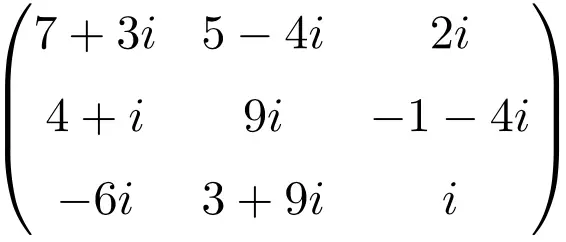
Пример комплексной матрицы размером 4х4

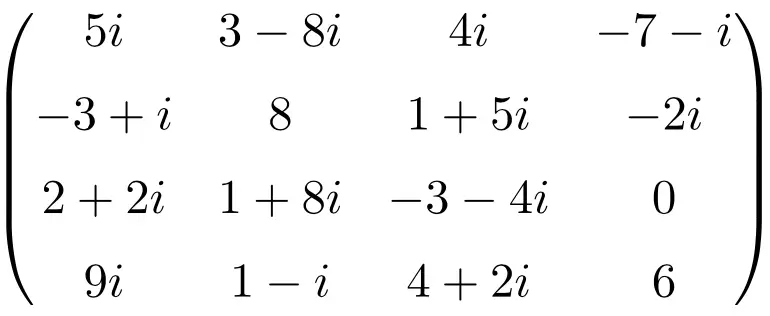
сопряженная матрица

После того, как мы поняли, что такое комплексная матрица, давайте посмотрим, что такое сопряженная матрица и транспонированная сопряженная матрица:

Что такое сопряженная матрица?

Сопряженная матрица — это комплексная матрица, в которой все ее элементы заменены сопряженными, то есть изменен знак мнимой части всех ее комплексных чисел.

Сопряженная матрица

$A$

выражается горизонтальной чертой выше:

$\overline{A}$

Пример сопряженной матрицы

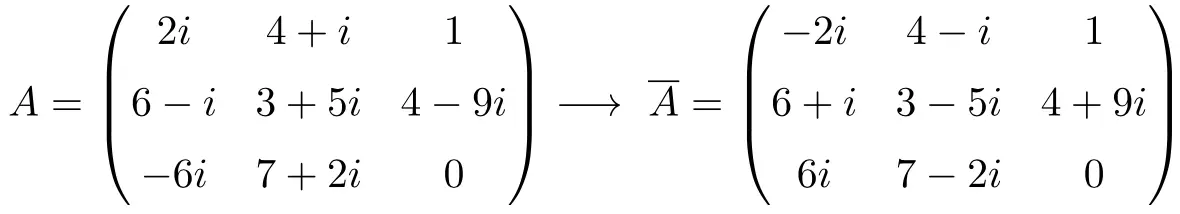
пример сопряжения матрицы, как сопрягать матрицу

Свойства сопряженной матрицы

Характеристики этого типа матрицы следующие:

Сопряженная сопряженная матрица является исходной матрицей.

$\displaystyle \overline{\bigl( \ \overline{A} \vphantom{A^{9^1}} \ \bigr)} = A$

Сложение (или вычитание) двух матриц и сопряжение результата аналогично сначала сопряжению двух матриц по отдельности, а затем их добавлению (или вычитанию).

$\displaystyle \overline{\bigl( A \pm B \bigr)} = \overline{A} \pm \overline{B}$

Сопряженное произведение двух матриц равно сопряжению двух матриц по отдельности и последующему вычислению умножения матриц.

$\displaystyle \overline{\bigl( A \cdot B \bigr)} = \overline{A} \cdot \overline{B}$

Умножение матрицы на скаляр и сопряжение результата — это то же самое, что сначала выполнить сопряжение скаляра и матрицы, а затем найти произведение.

$\displaystyle \overline{\bigl( k \cdot A \bigr)} = \overline{k} \cdot \overline{A}$

Транспонирование матрицы , а затем ее сопряжение означает сначала сопряжение матрицы, а затем ее транспонирование.

$\displaystyle \overline{\bigl(A^t \bigr)} = \left( \overline{A}\right)^t$

Выполнение обратной операции с матрицей и ее сопряжение — это то же самое, что сопряжение матрицы с последующим ее инвертированием.

$\displaystyle \overline{\bigl( A^{-1} \bigr)} = \left(\overline{A} \right)^{-1}$

Ранг сопряженной матрицы равен рангу той же несопряженной матрицы.

$\displaystyle rg\left(\overline{A}\right) =rg(A)$

Безразлично вычислить след сопряженной матрицы или вычислить след той же матрицы без сопряжения и затем сопрягать результат.

$\displaystyle tr\left(\overline{A}\right) =\overline{tr(A)}$

Наконец, взятие определителя сопряженной матрицы равносильно вычислению сопряженного результата определителя той же матрицы без сопряжения.

$\displaystyle det\left(\overline{A}\right) = \overline{det(A)}$

Сопряженная транспонированная матрица

Наконец, после того, как мы увидели, как сопрягать матрицу, давайте перейдем к понятию сопряженной транспонированной матрицы:

Что такое сопряженная транспонированная (или транспонированная) матрица?

Транспонированная (или транспонированная) сопряженная матрица — это матрица, полученная после транспонирования матрицы и последующего ее сопряжения.

Этот тип матрицы еще называют сопряженной матрицей или просто сопряженной матрицей. Кроме того, он обычно обозначается звездочкой

$(A^*)$

, хотя есть математики, которые рисуют это как

$A^*$

или

$A^H$

Пример матрицы сопряженного транспонирования

Вот пример вычисления транспонирования (или сопряженного транспонирования) матрицы:

$\displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}$

Сначала транспонируем матрицу A:

$\displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}$

А затем вычисляем сопряженную матрицу транспонирования или другими словами меняем знак мнимой части всех комплексных чисел:

$\displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}$

Таким образом, сводка расчета сопряженной транспонированной матрицы такова:

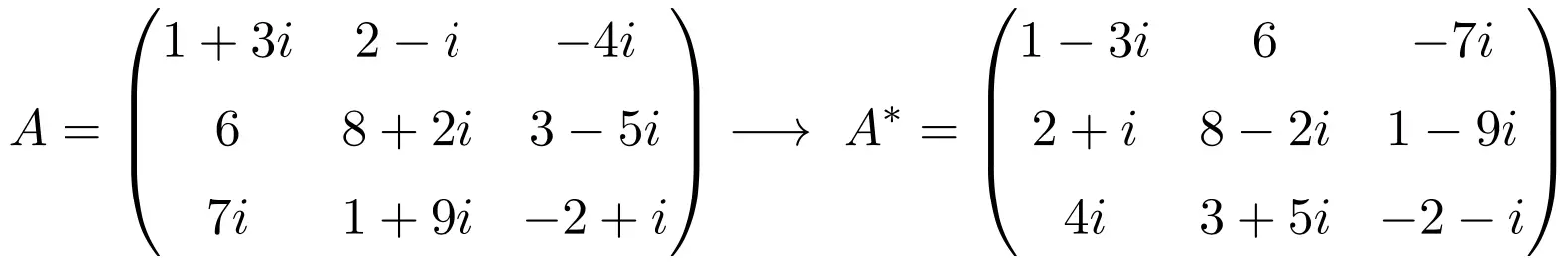
сопряженная транспонированная матрица размером 3х3

Свойства сопряженной транспонированной матрицы

Свойства этого типа квадратной матрицы следующие:

Сопряженная транспонированная матрица ранее транспонированной и сопряженной матрицы является исходной матрицей.

$\displaystyle \bigl(A^*\bigr) ^* = A$

Свойство сложения сопряженных транспонированных матриц гласит, что добавление (или вычитание) двух матриц и последующее применение этой операции к результату эквивалентно сначала выполнению сопряженного транспонирования каждой матрицы, а затем добавлению (или вычитанию) результатов.

$\displaystyle \bigl( A\pm B \bigr)^* = A^*\pm B^*$

Умножение двух матриц и последующее их сопряженное транспонирование дает тот же результат, что и обратное произведение сопряженных транспонированных матриц.

$\displaystyle \bigl( A\cdot B \bigr)^* = B^*\cdot A^*$

Вычисление сопряженной транспонированной матрицы произведения скаляра и матрицы аналогично сопряжению комплексного числа и нахождению сопряженной транспонированной матрицы отдельно с последующим умножением.

$\displaystyle \bigl( k\cdot A \bigr)^* = \overline{k}\cdot A^*$

Если матрица обратима, то порядок выполнения операций обращения матрицы и сопряженного транспонирования не имеет значения.

$\displaystyle \bigl( A^{-1} \bigr)^*= \bigl( A^* \bigr)^{-1}$