Регулярная или обратимая матрица

На этой странице вы найдете объяснение правильной или обратимой матрицы и то, как узнать, когда можно выполнить обращение матрицы, а когда нет. Кроме того, вы также увидите несколько примеров регулярных матриц, чтобы полностью понять концепцию, и, наконец, мы покажем вам все свойства матриц этого типа.

Что такое регулярная матрица?

Определение регулярной матрицы следующее:

Регулярная матрица — это квадратная матрица, которую можно инвертировать, т. е. можно вычислить обратную матрицу. Следовательно, его определитель не равен нулю (0).

Регулярные матрицы также называют обратимыми, неособыми или невырожденными матрицами .

Противоположной регулярной матрице является сингулярная или вырожденная матрица.

Таким образом, чтобы узнать, является ли матрица регулярной или сингулярной, то есть когда матрица обратима или нет, достаточно решить определитель матрицы:

Если определитель матрицы ненулевой, матрица правильная или обратимая.

Если определитель матрицы равен нулю, матрица сингулярна или необратима.

В заключение, вычисление определителя матрицы — это самый простой способ узнать, имеет ли матрица обратную или нет, поэтому именно это мы рекомендуем для определения обратимости любой матрицы.

Если вы хотите узнать, как инвертировать матрицу, вы можете ознакомиться с формулой обратной матрицы , которая шаг за шагом объясняет, как инвертировать матрицу, а также вы найдете несколько примеров и решенных упражнений для практики.

Примеры регулярных или обратимых матриц

После того, как мы поняли значение регулярной или обратимой матрицы, давайте посмотрим несколько примеров регулярных матриц разных размерностей:

Пример регулярной или обратимой матрицы 2×2.

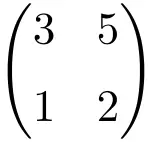
Мы можем убедиться, что это правильная матрица, вычислив ее определитель:

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

Определитель матрицы 2-го порядка отличен от 0, поэтому это обычная матрица.

Пример регулярной или обратимой матрицы 3×3.

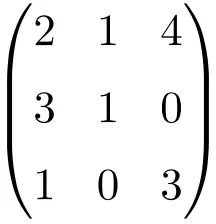
пример регулярной или обратимой матрицы размерности 3x3

Мы должны определить определитель матрицы, чтобы убедиться, что это обратимая матрица:

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

Определитель матрицы порядка 3 дает результат, отличный от 0, поэтому это регулярная матрица.

Пример регулярной или обратимой матрицы 4×4.

пример регулярной или обратимой матрицы размерности 4x4

Взятие определителя матрицы показывает, что это правильная матрица:

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

Определитель матрицы 4-го порядка не равен нулю, поэтому она является обратимой матрицей.

Внимание: если у вас есть сомнения по поводу расчета определителей, вы можете обратиться к странице , как вычислить определитель .

Свойства регулярных или обратимых матриц.

Регулярные или обратимые матрицы очень важны для линейной алгебры, и это связано со следующими характеристиками:

Если A является обратимой матрицей, то же самое относится и к ее транспонированной или транспонированной матрице. Кроме того, обратная матрица транспонирования равна транспонированию обратного.

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

Диапазон обычной матрицы всегда максимально возможный, или другими словами, диапазон эквивалентен размерности матрицы.

Матричное произведение двух обратимых матриц дает начало другой регулярной матрице. Это условие легко продемонстрировать с помощью свойств определителей:

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

Каждая ортогональная матрица одновременно является регулярной матрицей.

Пусть A — матрица, представляющая систему линейных уравнений
$(Ax=b)$

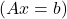
, если A — регулярная матрица, система имеет единственное решение, следовательно, это совместимая определительная система (SCD).

Более того, если система является однородной системой
$(Ax=0)$

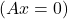
и A можно обратить, решение системы тривиально:

$x=0.$

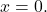
Столбцы и строки регулярной матрицы линейно независимы друг от друга.

Все собственные значения (или собственные значения) регулярной или обратимой матрицы отличны от нуля.

Обычная золотая обратимая матрица