Квадратное уравнение или квадратное уравнение – это уравнение степени 2, у которого наибольший показатель степени одного из его членов равен 2. Это означает, что уравнение может иметь до двух различных решений, хотя оно может иметь и единственное решение или вовсе нет.
Чтобы вычислить решения или корни квадратных уравнений, мы можем использовать две разные процедуры: с помощью квадратной формулы или путем факторизации выражения . В этой статье мы поговорим об обоих методах и дадим вам несколько практических упражнений. Однако прежде чем мы собираемся прояснить некоторые понятия, чтобы все объяснение было очень хорошо понятно и вы получили максимальную пользу от чтения.
Типы квадратных уравнений
Основная классификация квадратных уравнений основана на структуре самого выражения. Таким образом, стандартная или обычная структура этих выражений такова: ax² + bx + c . Эта общая форма эквивалентна полному уравнению, но когда есть нулевые или нулевые члены, структура может меняться, и именно здесь появляются неполные уравнения. Далее мы опишем характеристики всех типов более подробно.
Полные квадратные уравнения
Как мы уже говорили, у нас есть полные квадратные уравнения , у которых все коэффициенты a, b и c не равны нулю. Таким образом, выражение соответствует структуре ax² + bx + c до буквы, поскольку в нем есть все члены: квадратичный член, линейный член и независимый член. Примером такого типа является следующее уравнение: x² + 2x + 1 = 0.
Неполные квадратные уравнения
Что касается неполных уравнений, то их можно различать по тому, какой коэффициент равен нулю. Помните, что если это объяснение не разрешит ваши сомнения, чуть ниже находится изображение, на котором вы можете найти все случаи, объясненные шаг за шагом.
- Неполные уравнения (b = 0): в этой первой ситуации мы находим выражение, которое имеет следующую структуру: ax² + c = 0. При этом мы получаем два результата: отрицательный и положительный результат корня дроби c/a. .
- Неполные уравнения (c = 0): когда мы имеем форму ax² + bx = 0, мы должны факторизовать уравнение, чтобы оно имело выражение x (ax + b) = 0. Таким образом, у нас будет два решения: x = 0 и x = — б/а.
- Неполные уравнения (b = c = 0): в этом случае у нас есть уравнение ax² = 0, и у нас есть только одно возможное решение — x = 0.
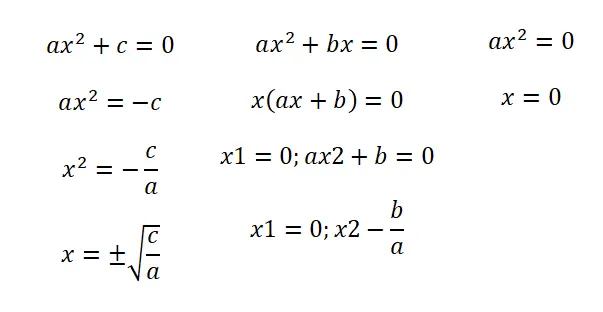
Стоит отметить, что процедуры, которым мы вас научили, позволяют вам быстрее решать неполные уравнения. Но во всех случаях вы можете использовать квадратную формулу , которой мы вас научим ниже, вам нужно будет только написать ноль в коэффициентах, которых нет.
Формула для квадратных уравнений
Для решения квадратных уравнений (ax² + bx + c = 0) нам нужно применить общую формулу или квадратную формулу, а затем нам нужно подставить числовые значения , соответствующие каждой букве в математическом выражении.
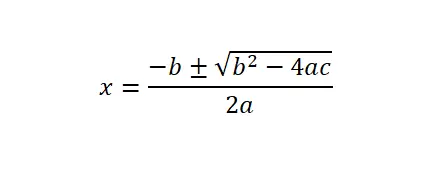
Также важно пояснить, что дискриминантом (Δ) является выражение b² – 4ac, которое находится под квадратным корнем. Из этой математической концепции мы можем узнать, сколько решений имеет это квадратное уравнение. По сути, есть три варианта: дискриминант отрицательный (действительных решений нет), дискриминант нулевой (решение только одно) или дискриминант положительный (существует два решения).
Пример решения полного квадратного уравнения
Попробуйте решить следующее квадратное уравнение: 2x²+4x-6=0 и сверьте свой результат с приведенным ниже. Мы рекомендуем вам выполнить следующую процедуру: проанализировать тип уравнения (определить нулевые члены), вычислить дискриминант, чтобы узнать количество существующих решений и, наконец, решить предложенное уравнение по формуле.
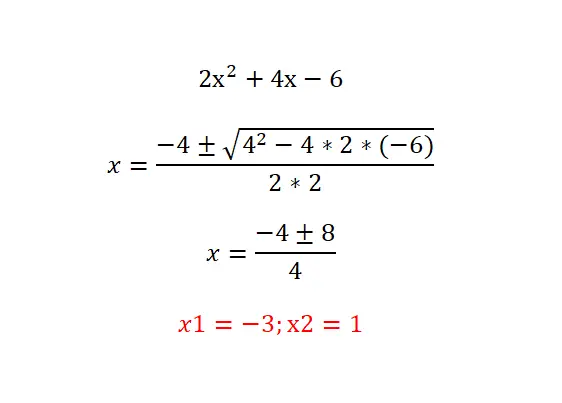
Факторные квадратные уравнения
Второй метод решения квадратных уравнений — факторизация . Итак, для факторизации многочлена (в нашем случае квадратного многочлена) мы можем использовать разные методы. Хотя в целом, когда речь идет об уравнениях такого типа, их обычно факторизуют по общему члену. А если нет, вы можете попробовать применить Notable Identities , но обычно в таких ситуациях вам не нужно знать никаких других методов.
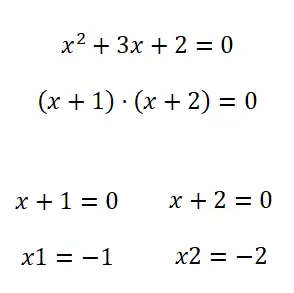
Упражнения с квадратными уравнениями с решениями
Ниже вы найдете серию упражнений по полным и неполным квадратным уравнениям . Таким образом, вы повторите всю теорию, изложенную в этой статье, и вам будет яснее, как применять ее в упражнениях. Мы рекомендуем вам попытаться решить их самостоятельно и смотреть на решение только тогда, когда вы их выполнили или когда вы застряли. Тем не менее, вы можете начать решать упражнения прямо сейчас.
Упражнение 1
Решите следующее квадратное уравнение:
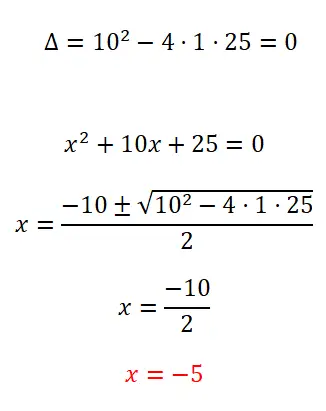
- Начнем с вычисления дискриминанта, чтобы узнать количество возможных решений.
- Поскольку это полное квадратное уравнение, применим квадратную формулу и решим вычисления.
- Получаем значение неизвестного x.
Упражнение 2
Решите следующее квадратное уравнение:
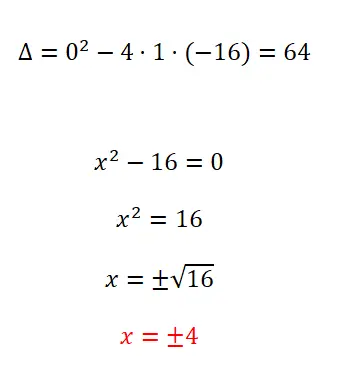
- Начнем с вычисления дискриминанта.
- Поскольку мы имеем неполное квадратное уравнение, в котором b = 0, применим стандарт для уравнений такого типа.
- Мы решаем расчет, чтобы получить результат, и мы не можем забыть знак ±.
Упражнение 3
Решите следующее неупорядоченное квадратное уравнение:
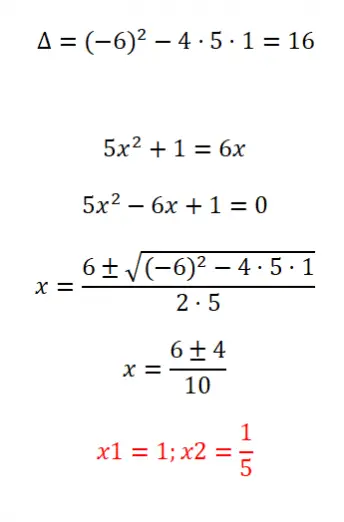
- Начнем с вычисления дискриминанта уравнения.
- Прежде чем мы сможем применить формулу, нам нужно упорядочить уравнение в соответствии со структурой ax² + bx + c = 0.
- Затем применяем общую формулу.
- И наконец мы получаем результаты.
Упражнение 4
Решите следующее квадратное уравнение методом факторизации:
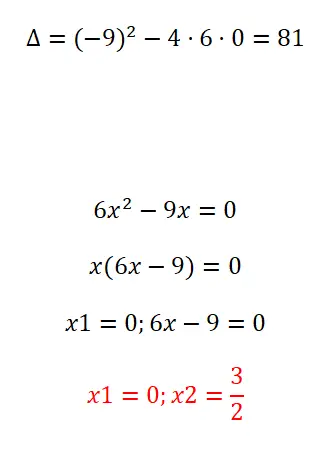
- Сначала вычислим дискриминант.
- Далее мы извлекаем общий множитель x.
- Итак, первое решение — x = 0.
- А второй — х = 3/2.
Упражнение 5
Решите полное квадратное уравнение, которое мы покажем ниже:
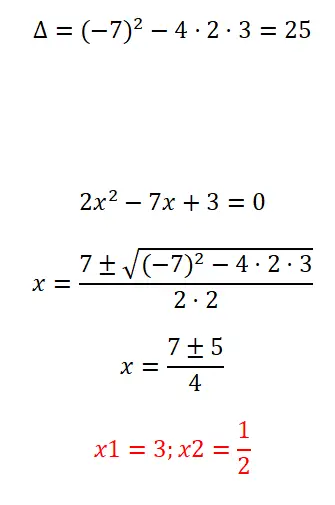
- Как всегда, вычисляем дискриминант, чтобы узнать, сколько решений имеет рассматриваемое уравнение.
- Далее применим квадратную формулу, так как это полное уравнение.
- Наконец, выразим результат уравнения.
Упражнение 6
Решите квадратное уравнение с дробями, которые мы предлагаем:
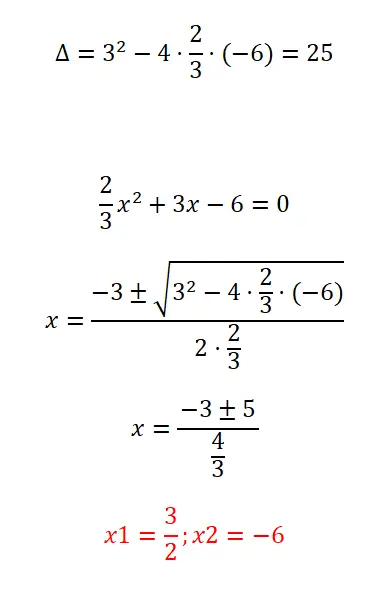
- Начнем с вычисления дискриминанта выражения.
- Далее применяем квадратичную формулу, учитывая, что коэффициент «а» образован дробью.
- Решаем расчет.
- И у нас уже есть два корня уравнения.
Упражнение 7
Решите следующее квадратное уравнение:
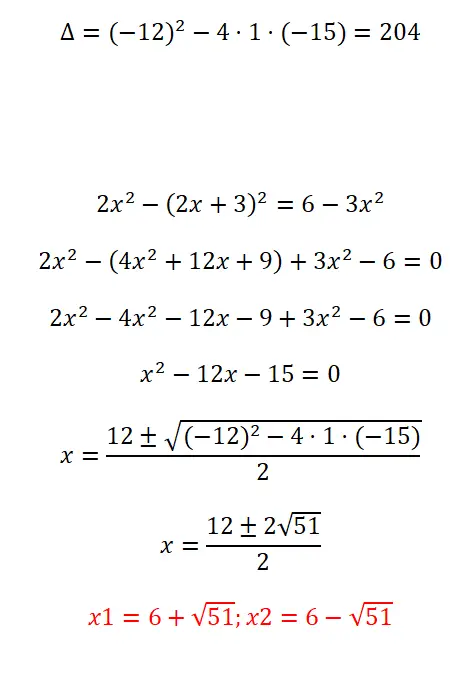
- Начнем с вычисления дискриминанта.
- Прежде чем применять формулу, нам необходимо упростить выражение и придать ему вид ax² + b + c = 0.
- Подставляем все коэффициенты в формулу и решаем расчет.
- Наконец мы получаем результат.
Упражнение 8
Доказательство решения следующего квадратного уравнения:
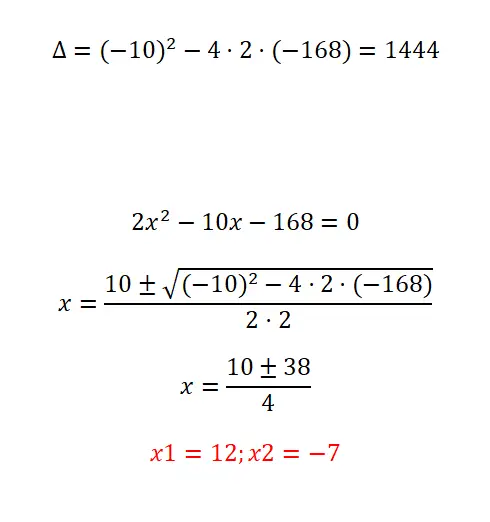
- Начнем с вычисления дискриминанта.
- Как видите, это простое квадратное уравнение, хотя и имеет довольно большие коэффициенты. Поэтому нам нужно применять формулу и быть осторожными при выполнении операций.
- В итоге мы получаем оба возможных решения.