Здесь вы найдете объяснение того, что представляет собой формула канонического (или сегментного) уравнения линии, называемого также симметричным уравнением. Кроме того, вы сможете увидеть примеры и попрактиковаться на решенных упражнениях. И даже вы узнаете, как каноническое уравнение вычисляется из общего (или неявного) уравнения линии.
Что такое каноническое или сегментное уравнение прямой?
Помните, что математическое определение линии — это набор последовательных точек, которые представлены в одном направлении без кривых или углов.
Таким образом, каноническое уравнение линии , также называемое сегментным уравнением линии , представляет собой способ математического выражения любой линии. Для этого достаточно знать точки пересечения координатных осей указанной линии.
С другой стороны, в аналитической геометрии каноническое (или сегментное) уравнение линии еще называют симметричным уравнением линии .
Формула канонического или сегментного уравнения прямой
Каноническое или сегментное уравнение линии — это алгебраическое выражение линии, которое можно определить, зная значения, в которых линия пересекает ось X и ось Y.
Если линия пересекает декартовы оси в следующих точках:
Точка пересечения с осью X:
![]()
Точка пересечения с осью Y:
![]()
Формула канонического (или сегментного) уравнения линии :
![]()

Следует отметить, что канонического (или сегментного) уравнения линии не существует ни в одном из следующих трех случаев:
- Когда линия вертикальна, то есть параллельна оси OY. Поскольку уравнение вертикальной линии имеет вид

- Когда линия горизонтальна, то есть параллельна оси OX. Поскольку уравнение горизонтальной линии имеет вид

- Когда линия проходит через начало координат (точку
), так как тогда мы имели бы две неопределенности в уравнении прямой.
Пример того, как найти каноническое или сегментное уравнение прямой
Чтобы вы лучше поняли концепцию, решим задачу сегментного (или канонического) уравнения прямой:
- Найдите каноническое или сегментное уравнение прямой, проходящей через следующие две точки:
![]()
В этом случае объявление дает нам не 2 точки, а две точки пересечения с осями.
Точка пересечения линии с осью X:
![]()
Точка пересечения линии с осью Y:
![]()
Итак, поскольку мы уже знаем две точки пересечения осей, нам просто нужно применить формулу канонического или сегментного уравнения линии:
![]()
И наконец, подставляем значения параметров
![]()
И
![]()
в формуле:
![]()
Теперь вы знаете, что такое каноническое (или сегментное) уравнение прямой. Однако следует знать, что существуют и другие способы выражения линии, и среди них выделяется явное уравнение . Этот тип линейного уравнения трудно полностью понять, поэтому мы подробно объяснили все о нем на связанной странице.
Рассчитайте каноническое или сегментное уравнение линии из ее общего уравнения.
Мы только что рассмотрели способ определения канонического или сегментного уравнения прямой, но есть и другие методы:
Каноническое или сегментное уравнение линии можно получить из общего (или неявного) уравнения этой же линии:
![]()
Сначала меняем стороны по коэффициенту С:
![]()
Далее разделим все уравнение на значение знакопеременного параметра C:
![]()
![]()
И, через свойства дробей, приходим к формуле канонического или сегментного уравнения прямой:
![]()
Следовательно, из этой формулы следует, что члены
![]()
И
![]()
канонического уравнения прямой эквивалентны следующим выражениям:
![]()
Решенные задачи канонического или сегментного уравнения прямой
Упражнение 1
Каковы точки пересечения с осями координат следующей прямой?
![]()
Линия в упражнении выражается в виде канонического или сегментного уравнения линии, формула которого имеет вид:
![]()
Следовательно, точки пересечения прямой с осями координат составляют:
Точка пересечения с осью X:
![]()
Точка пересечения с осью Y:
![]()
Упражнение 2
Какое каноническое или сегментное уравнение изображенной линии?
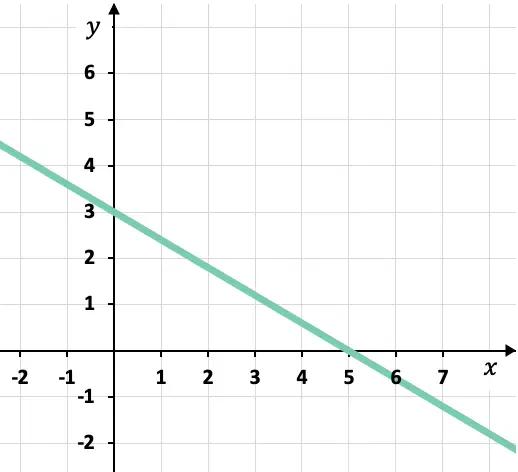
Из графика мы можем узнать точки, в которых линия пересекает оси координат:
Точка пересечения линии с осью X:
![]()
Точка пересечения линии с осью Y:
![]()
Итак, как только мы уже знаем две точки пересечения осей, нам просто нужно использовать формулу канонического или сегментного уравнения линии:
![]()
И наконец, подставляем значения параметров
![]()
И
![]()
в формуле:
![]()
Упражнение 3
Рассчитайте каноническое или сегментное уравнение линии, определяемой следующим общим (или неявным) уравнением:
![]()
Чтобы перейти от общего уравнения к сегментному уравнению, мы должны сначала выделить независимый член уравнения:
![]()
![]()
Во-вторых, разделим все уравнение на коэффициент в правой части уравнения:
![]()
![]()
Выражение выше эквивалентно следующему:
![]()
Итак, каноническое, сегментное или симметричное уравнение линии:
![]()
Упражнение 4
Определите каноническое или сегментное уравнение, вектор направления которого равен
![]()
и проходит через точку
![]()
Сначала легко находим непрерывное уравнение прямой по ее вектору направления и точке, принадлежащей прямой:
![]()
![]()
![]()
Теперь вычислим общее уравнение линии, умножив дроби крест-накрест и сгруппировав полученные члены:
![]()
![]()
![]()
![]()
Поэтому достаточно преобразовать общее уравнение линии в каноническое уравнение. Для этого сначала удалим из уравнения независимый член:
![]()
Далее разделим все уравнение на коэффициент в правой части уравнения:
![]()
![]()
Выражение выше эквивалентно следующему:
![]()
Отрицательное, разделенное на отрицательное, равно положительному:
![]()
Дроби не могут быть упрощены дальше, поэтому каноническое, сегментное или симметричное уравнение прямой имеет вид:
![]()