Как диагонализировать матрицу -

На этой странице вы найдете все о диагонализуемых матрицах: что это такое, когда их можно диагонализировать, а когда нельзя, способ диагонализации матриц, приложения и свойства именно этих матриц и т. д. И у вас даже есть несколько упражнений, решенных шаг за шагом, чтобы вы могли потренироваться и прекрасно понять, как они диагонализуются. Наконец, мы также научимся выполнять диагонализацию матриц с помощью компьютерной программы MATLAB, поскольку она очень часто используется.

Что такое диагонализуемая матрица?

Как мы увидим ниже, диагонализация матрицы очень полезна в области линейной алгебры. Поэтому многие спрашивают… что такое диагонализация матрицы? Итак, определение диагонализируемой матрицы таково:

Диагонализуемая матрица — это квадратная матрица, которую можно преобразовать в диагональную матрицу, то есть матрицу, заполненную нулями, кроме главной диагонали. Диагонализация матриц разбивается следующим образом:

$A = PDP^{-1}$

Или эквивалент,

$D = P^{-1}AP$

Золото

$A$

— матрица для диагонализации,

$P$

— матрица, столбцы которой являются собственными векторами (или собственными векторами) матрицы

$A$

$P^{-1}$

ее обратная матрица и

$D$

— диагональная матрица, образованная собственными значениями (или собственными значениями)

$A$

Матрица

$P$

действует как матрица изменений базы, поэтому на самом деле с помощью этой формулы мы меняем базу на матрицу

$A$

, так что матрица становится диагональной (

$D$

) в новой базе.

Следовательно, матрица

$A$

и матрица

$D$

Это аналогичные матрицы. И очевидно,

$P$

Это регулярная или невырожденная матрица.

Когда можно диагонализировать матрицу?

Не все матрицы можно диагонализировать; только матрицы, отвечающие определенным характеристикам, могут быть диагонализированы. Определить, является ли матрица диагонализуемой, можно разными способами:

Квадратная матрица порядка n является диагонализируемой, если она имеет n линейно независимых собственных векторов (или собственных векторов) , или, другими словами, если эти векторы образуют базис. Это потому, что матрица
$P$

, который используется для диагонализации матрицы, формируется собственными векторами указанной матрицы. Чтобы узнать, являются ли собственные векторы LI, достаточно, чтобы определитель матрицы

$P$

отлично от 0, что означает, что матрица имеет максимальный ранг.

$\text{si} \quad \text{det}(P)\neq 0 \ \longrightarrow \ \text{matriz diagonalizable}$

Свойством собственных значений и собственных векторов является то, что собственные векторы разных собственных значений линейно независимы. Следовательно, если все собственные значения матрицы уникальны, матрица диагонализируема.

Другой способ определить, можно ли разместить матрицу в диагональной матрице, — использовать алгебраическую и геометрическую кратности. Алгебраическая кратность — это количество повторений собственного значения (или собственного значения), а геометрическая кратность — это размерность ядра (или ядра) матрицы путем вычитания собственного значения на ее главной диагонали. Таким образом, если для каждого собственного значения алгебраическая кратность равна геометрической кратности , матрица является диагонализуемой.

$\alpha_\lambda = \text{multiplicidad algebraica} = \text{multiplicidad del valor propio}$

$m_\lambda = \text{multiplicidad geom\'etrica} = \text{dim } Ker(A-\lambda I) = n -rg(A-\lambda I)$

$\alpha_\lambda \geq m_\lambda \geq 1$

$\text{si} \quad \alpha_\lambda = m_\lambda \quad \forall \lambda \ \longrightarrow \ \text{matriz diagonalizable}$

Наконец, существует теорема — спектральная теорема, гарантирующая диагонализацию симметричных матриц с действительными числами. Другими словами, любая действительная и симметричная матрица диагонализуема .

Как диагонализировать матрицу

Процедура диагонализации матрицы основана на нахождении собственных значений (или собственных значений) и собственных векторов (или собственных векторов) матрицы. Вот почему важно, чтобы вы научились вычислять собственные значения (или собственные значения) и собственные векторы (или собственные векторы) любой матрицы . Вспомнить, как это делалось, можно, перейдя по ссылке, где мы пошагово объясним, как их найти и некоторые хитрости, значительно упрощающие расчеты. Кроме того, вы также найдете решенные упражнения для практики.

Следующим методом можно диагонализировать матрицу любой размерности: 2х2, 3х3, 4х4 и т. д. Шаги, которые необходимо выполнить для диагонализации матрицы:

Получите собственные значения (или собственные значения) матрицы.
Вычислите собственный вектор, связанный с каждым собственным значением.
Постройте матрицу
$P$

, столбцы которого являются собственными векторами матрицы, подлежащей диагонализации.
Убедитесь, что матрица может быть диагонализирована (она должна соответствовать одному из условий, описанных в предыдущем разделе).
Постройте диагональную матрицу
$D$

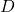
, все элементы которого равны 0, кроме элементов на главной диагонали, которые являются собственными значениями, найденными на шаге 1.

Внимание: собственные векторы матрицы

$P$

можно располагать в любом порядке, но собственные значения диагональной матрицы

$D$

Их необходимо расположить в том же порядке. Например, первое собственное значение диагональной матрицы

$D$

должен быть тот, который соответствует собственному вектору первого столбца матрицы

$P$

Ниже приведены несколько пошаговых упражнений по диагонализации матрицы, с которыми вы можете попрактиковаться.

Решение упражнений по диагонализации матрицы

Упражнение 1

Диагонализуйте следующую квадратную матрицу размером 2×2:

$\displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}$

Посмотреть решение

Сначала мы должны определить собственные значения матрицы A. Поэтому мы вычисляем характеристическое уравнение, решив следующий определитель:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4$

Теперь вычислим корни характеристического многочлена:

$\displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}$

Как только собственные значения получены, мы вычисляем собственный вектор, связанный с каждым. Во-первых, собственный вектор, соответствующий собственному значению 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}$

А затем вычисляем собственный вектор, связанный с собственным значением 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}$

Строим матрицу

$P$

, образованный собственными векторами матрицы:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}$

Поскольку все собственные значения различны, матрица А диагонализуема. Таким образом, соответствующей диагональной матрицей является та, у которой собственные значения находятся на главной диагонали:

$\displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Помните, что собственные значения должны располагаться в том же порядке, в каком располагаются собственные векторы в матрице.

$P$

В заключение, матрица изменения базиса и диагонализированная матрица:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Упражнение 2

Диагонализуйте следующую квадратную матрицу второго порядка:

$\displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}$

Посмотреть решение

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2$

Теперь вычислим корни характеристического многочлена:

$\displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}$

Как только собственные значения получены, мы вычисляем собственный вектор, связанный с каждым. Во-первых, собственный вектор, соответствующий собственному значению -1:

$\displaystyle (A+I)v=0$

$\displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}$

А затем вычисляем собственный вектор, связанный с собственным значением 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y$

$\displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}$

Строим матрицу

$P$

, образованный собственными векторами матрицы:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}$

Поскольку все собственные значения отличны друг от друга, матрица А диагонализуема. Таким образом, соответствующей диагональной матрицей является та, которая содержит собственные значения на главной диагонали:

$\displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

$P$

В заключение, матрица изменения базиса и диагонализированная матрица:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Упражнение 3

Диагонализуйте следующую квадратную матрицу размером 3×3:

$\displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}$

Посмотреть решение

Первый шаг состоит в нахождении собственных значений матрицы A. Поэтому мы вычисляем характеристическое уравнение, решая определитель следующей матрицы:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12$

Теперь нам нужно вычислить корни характеристического многочлена. Поскольку это полином третьей степени, применим правило Руффини:

$\displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}$

А затем находим корни полученного многочлена:

$\displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}$

Итак, собственные значения матрицы:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 4$

После того как собственные значения найдены, вычисляем собственный вектор, связанный с каждым из них. Во-первых, собственный вектор, соответствующий собственному значению 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}$

Затем мы вычисляем собственный вектор, связанный с собственным значением 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

И, наконец, вычисляем собственный вектор, связанный с собственным значением 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}$

Строим матрицу

$P$

, образованный собственными векторами матрицы:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}$

Поскольку все собственные значения отличны друг от друга, матрица А диагонализуема. Таким образом, соответствующей диагональной матрицей является та, у которой собственные значения находятся на главной диагонали:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

$P$

Короче говоря, матрица изменения базиса и диагонализованная матрица:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Упражнение 4

Диагонализуйте, если возможно, следующую квадратную матрицу третьего порядка:

$\displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}$

Посмотреть решение

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8$

Теперь нам нужно вычислить корни минимального многочлена. Поскольку это полином третьей степени, мы применяем правило Руффини для его факторизации:

$\displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}$

А затем находим корни полученного многочлена:

$\displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}$

Итак, собственные значения матрицы:

$\lambda=2 \qquad \lambda =2 \qquad \lambda = -2$

Собственное значение -2 имеет простую алгебраическую кратность, с другой стороны, собственное значение 2 имеет двойную кратность.

$\displaystyle (A+2I)v=0$

$\displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}$

Давайте теперь вычислим собственные векторы, связанные с собственными значениями 2.

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}$

Поскольку собственное значение 2 повторяется дважды, нам нужно вычислить другой собственный вектор, который удовлетворяет уравнениям подпространства (или собственного пространства):

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}$

Строим матрицу

$P$

, образованный тремя собственными векторами матрицы:

$\displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}$

Однако эти три вектора не являются линейно независимыми, поскольку очевидно, что два собственных вектора с собственным значением 2 представляют собой линейную комбинацию друг друга. Это также можно продемонстрировать, поскольку определитель матрицы

$P$

равно 0 (имеет строку, полную нулей):

$\displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0$

Следовательно, поскольку собственные векторы линейно зависимы, матрица A не является диагонализуемой .

Упражнение 5

Если возможно, диагонализуйте следующую квадратную матрицу размером 3×3:

$\displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}$

Посмотреть решение

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}$

Поскольку первая строка полностью состоит из нулей, кроме 3, мы воспользуемся этим для решения определителя матрицы с помощью сомножителей (или сопряженных):

$\displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}$

Теперь нам нужно вычислить корни характеристического многочлена. Скобки лучше не умножать, так как тогда вы получите полином третьей степени. С другой стороны, если два фактора решаются отдельно, легче получить собственные значения:

$\displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}$

Итак, собственные значения матрицы:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 3$

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Затем вычисляем собственные векторы, связанные с собственными значениями 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}$

Поскольку собственное значение 3 повторяется дважды, нам нужно вычислить другой собственный вектор, который удовлетворяет уравнениям собственного пространства:

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

Строим матрицу

$P$

, образованный собственными векторами матрицы:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}$

В отличие от упражнения 4, в этом случае нам удалось сформировать 3 линейно независимых вектора, хотя алгебраическая кратность собственного значения 3 двойная. В этом можно убедиться, увидев, что определитель матрицы

$P$

дает результат, отличный от 0:

$\displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0$

Таким образом, мы можем провести диагональное разложение матрицы А. И соответствующая диагональная матрица — это та, у которой собственные значения находятся на главной диагонали:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

$P$

Короче говоря, матрица изменения базиса, необходимая для диагонализации матрицы и ее диагонализированной формы, такова:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Упражнение 6

Провести диагонализацию, если это возможно, следующей матрицы размерности 4×4:

$\displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Посмотреть решение

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}$

В этом случае последний столбец определителя состоит только из нулей, за исключением одного элемента, поэтому мы воспользуемся этим для вычисления определителя по сомножителям через этот столбец:

$\displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}$

Теперь нам нужно вычислить корни характеристического многочлена. Произведение скобок лучше не делать, потому что тогда вы получите многочлен четвертой степени. Однако, если два фактора решаются отдельно, собственные значения легче вычислить:

$\displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}$

$\displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}$

Итак, собственные значения матрицы:

$\lambda=0 \qquad \lambda =-3 \qquad \lambda = 2\qquad \lambda = 5$

После того как все собственные значения найдены, переходим к собственным векторам. Вычисляем собственный вектор, связанный с собственным значением 0:

$\displaystyle (A-0I)v=0$

$\displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Вычисляем собственный вектор, связанный с собственным значением -3:

$\displaystyle (A+3I)v=0$

$\displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Вычисляем собственный вектор, связанный с собственным значением 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Вычисляем собственный вектор, связанный с собственным значением 5:

$\displaystyle (A-5I)v=0$

$\displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}$

Делаем матрицу

$P$

, составленный из собственных векторов матрицы:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}$

$\displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Помните, что собственные значения должны располагаться в том же порядке, в каком расположены собственные векторы в матрице

$P$

Таким образом, основные изменения матрицы, необходимые для диагонализации матрицы A и матрицы в диагональной форме, таковы:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Приложения диагонализуемых матриц

Если вы зашли так далеко, вы, вероятно, задаетесь вопросом: для чего нужна диагонализуемая матрица?

Что ж, диагонализуемые матрицы очень полезны и широко используются в математике. Причина в том, что диагональная матрица практически полна нулей и поэтому значительно упрощает вычисления.

Ярким примером этого являются степени диагонализуемых матриц, поскольку их результат упрощается следующей формулой:

$\displaystyle A^k=PD^kP^{-1}$

Это равенство легко доказывается по индукции. Поэтому достаточно поднять матрицу

$D$

экспоненту. А поскольку это диагональная матрица, то операция сводится к возведению каждого члена главной диагонали в показатель степени:

$\displaystyle D^k = diag(\lambda_1^k,\lambda_2^k, \ldots , \lambda_n^k)$

Пример степени диагонализуемой матрицы

Чтобы лучше понять, в качестве примера вычислим степень диагонализуемой матрицы:

$\displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}$

Матрица основных изменений

$P$

, образованная собственными векторами, и диагонализованной матрицей

$D$

, состоящий из собственных значений, являются:

$\displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}$

Итак, чтобы привести пример, матрица A, повышенная до 7, эквивалентна:

$\displaystyle A^7=PD^7P^{-1}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}$

Теперь инвертируем матрицу

$P:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

Решаем мощность матрицы

$D:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

И, наконец, выполняем умножения матриц:

$\displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}$

Как вы видели, вычислять степень с диагональной матрицей удобнее, чем умножать одну и ту же матрицу семь раз подряд. Затем представьте себе гораздо большие значения показателя степени.

Свойства диагонализуемых матриц

Характеристики этого типа матрицы:

Если матрица
$A$

диагонализуема, любая степень

$A$

.

Почти все матрицы можно диагонализовать в сложной среде.
$\mathbb{C}$

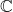
. Хотя ниже приведены исключения, которые никогда не поддаются диагонализации.

Если матрица
$P$

является ортогональной матрицей, то мы говорим, что матрица

$A$

ортогонально диагонализируема , поэтому уравнение можно переписать:

$\displaystyle A=PDP^t$

Матрица диагонализуема унитарной матрицей тогда и только тогда, когда она является нормальной матрицей.

Учитывая две диагонализуемые матрицы, они коммутативны тогда и только тогда, когда их можно диагонализовать одновременно, то есть если они имеют один и тот же ортонормированный базис собственных векторов (или собственных векторов).

Если эндоморфизм диагонализуем, мы говорим, что он диагонализуем по подобию . Однако не все эндоморфизмы диагонализуемы, или, другими словами, диагонализация эндоморфизма не гарантирована.

Одновременная диагонализация

Множество матриц называется одновременно диагонализируемым, если существует обратимая матрица, по которой можно провести диагонализацию любой матрицы из этого множества. Другими словами, если две матрицы диагонализуются по одному и тому же базису собственных векторов, это означает, что они диагонализуются одновременно.

Кроме того, как мы отметили в свойствах диагонализации матриц, если две матрицы способны одновременно диагонализовываться, они должны коммутировать друг с другом.

Например, следующие две матрицы перестановочны, поэтому они диагонализуются на одной и той же основе собственных векторов или собственных векторов.

$\displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}$

Даже если у них одинаковые собственные векторы, это не значит, что у них одинаковые собственные значения. Фактически, хотя приведенные выше матрицы A и B имеют схожие собственные векторы, они имеют разные собственные значения.

Недиагонализируемые матрицы

Хотя подавляющее большинство матриц диагонализуемы в среде комплексных чисел, некоторые матрицы никогда не могут быть диагонализуемы.

Этот факт имеет место, когда алгебраическая кратность собственного значения (или собственного значения) не совпадает с геометрической кратностью.

Например, следующую матрицу никак нельзя диагонализировать, она «недиагонализуема»:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}$

Кроме того, существуют матрицы, которые не способны к диагонализации в среде действительных чисел, но они диагонализуются при работе с комплексными числами, как эта матрица:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}$

Наконец, существуют некоторые процедуры диагонализации матричных блоков , которые не являются чисто диагонализуемыми, но немного сложнее. Самый известный метод — диагонализация с канонической формой Жордана .

Диагонализация матрицы с помощью MATLAB

Компьютерные программы очень удобны при диагонализации матриц, особенно если они очень большие. И самое известное программное обеспечение, безусловно, MATLAB , поэтому далее мы увидим, как с помощью этой программы факторизовать матрицу по диагонали.

Инструкция, используемая для диагонализации матрицы с помощью MATLAB:

$\displaystyle \text{[P, D] = eig(A)}$

Золото

$A$

— матрица, которую нужно диагонализировать, и

$P$

$D$

это матрицы, которые возвращает программа:

$P$

– матрица, образованная собственными векторами и

$D$

— матрица в диагональной форме, главные диагональные члены которой являются собственными значениями.

Поэтому вам просто нужно ввести этот код в программу.

С другой стороны, если вы хотите узнать только собственные значения, вы можете использовать следующий оператор:

$\displaystyle e= eig(A)}$

Золото

$e$

— вектор-столбец, который MATLAB возвращает с собственными значениями матрицы

$A$

Что такое диагонализуемая матрица?

Когда можно диагонализировать матрицу?

Как диагонализировать матрицу

Решение упражнений по диагонализации матрицы

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Упражнение 6

Приложения диагонализуемых матриц

Пример степени диагонализуемой матрицы

Свойства диагонализуемых матриц

Одновременная диагонализация

Недиагонализируемые матрицы

Диагонализация матрицы с помощью MATLAB

Оставьте комментарий Отменить ответ