Иррациональная функция или радикальная функция -

На этой странице объясняется, что такое иррациональная функция, также называемая радикальной функцией, а также все характеристики этого типа функции. Вы также узнаете, как вычислять область определения радикальных или иррациональных функций, и, кроме того, вы сможете увидеть, как представить их на графике с примерами и попрактиковаться в упражнениях и задачах, решаемых шаг за шагом.

Что такое иррациональная (или радикальная) функция?

Иррациональная функция означает то же самое, что и радикальная функция, и, следовательно, они имеют общее определение:

Иррациональная функция , также называемая радикальной функцией , — это функция, имеющая независимую переменную x под символом корня.

Как мы уже знаем, результат корня может быть положительным или отрицательным. Таким образом, представление иррациональной (или радикальной) функции имеет две возможные кривые:

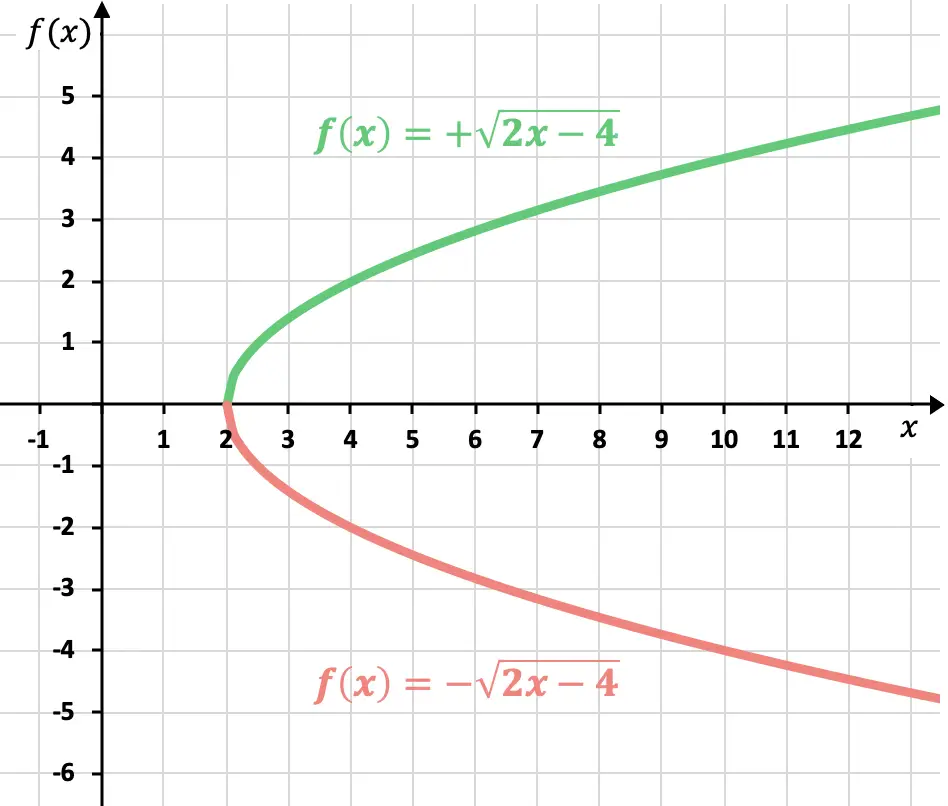
примеры иррациональных или радикальных функций

Но если знак не указан, предполагается, что представлена положительная функция.

С другой стороны, не следует путать иррациональную функцию с рациональной функцией. Хотя у них очень похожие имена, это два совершенно разных типа функций.

Область иррациональной или радикальной функции

Область определения функции с корнями зависит от четности индекса корня, т. е. от того, является ли радикальный индекс четным или нечетным.

Область определения функции с корнем из четного индекса

Как известно, у отрицательного числа не существует корня (даже индекса). Следовательно, радикальная функция с четным индексом будет существовать до тех пор, пока ее содержимое равно или больше 0.

В качестве примера давайте посмотрим, как вычисляется область определения следующей радикальной или иррациональной функции:

$f(x)=\sqrt{x-4}$

Это радикальная индексная функция, поэтому мы должны посмотреть, когда ее содержимое положительное или нулевое :

$x-4\ge 0$

Решаем неравенство:

$x\ge 4$

Таким образом, функция будет существовать всякий раз, когда x больше или равно 4, и обозначается следующим интервалом:

$\text{Dom } f= [4,+\infty)$

Область определения функции с корнем из нечетного индекса

Иррациональные функции с нечетным индексом не имеют этой проблемы, поскольку корень нечетного индекса отрицательного числа существует:

$\sqrt[3]{-8}=-2$

Следовательно, радикальные функции нечетного индекса существуют для любого значения x . Или, другими словами, домен состоит только из вещественных чисел .

Например, вычислим область определения следующей радикальной функции с нечетным индексом:

$f(x)=\sqrt[3]{3x-4}$

Поскольку это иррациональная функция с нечетным индексом, ее область определения состоит из действительных чисел:

$\text{Dom } f= \mathbb{R}$

Как представить иррациональную или радикальную функцию

Давайте посмотрим, как представить на графике функцию с корнями на примере.

Постройте на графике следующую радикальную или иррациональную функцию:

$f(x)=\sqrt{x+2}$

Первое, что нужно сделать, это найти область определения функции. Поскольку это квадратный корень, все, что в нем содержится, должно быть положительным, поскольку из отрицательного числа не существует квадратного корня. Следовательно, радикальная функция будет существовать до тех пор, пока ее содержимое равно или больше 0:

$x+2\ge 0$

$x\ge -2$

Таким образом, область определения функции состоит из всех чисел, больших или равных -2. Это сказать:

$\text{Dom } f = [-2,+\infty)$

Как только мы узнаем область определения функции, мы создаем таблицу значений. Очевидно, что чем больше точек мы вычислим, тем точнее будет представление функции. Но расчета 3 или 4 точек в интервале домена вполне достаточно:

$x= -2 \ \longrightarrow \ f(-2)=\sqrt{-2+2}= 0$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{-1+2}= 1$

$x= 2 \ \longrightarrow \ f(2)=\sqrt{2+2}= 2$

$x= 7 \ \longrightarrow \ f(7)=\sqrt{7+2}= 3$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 0 \\ -1 & 1 \\ 2 & 2 \\ 7 & 3 \end{array}$

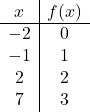
Теперь представим полученные точки на графике :

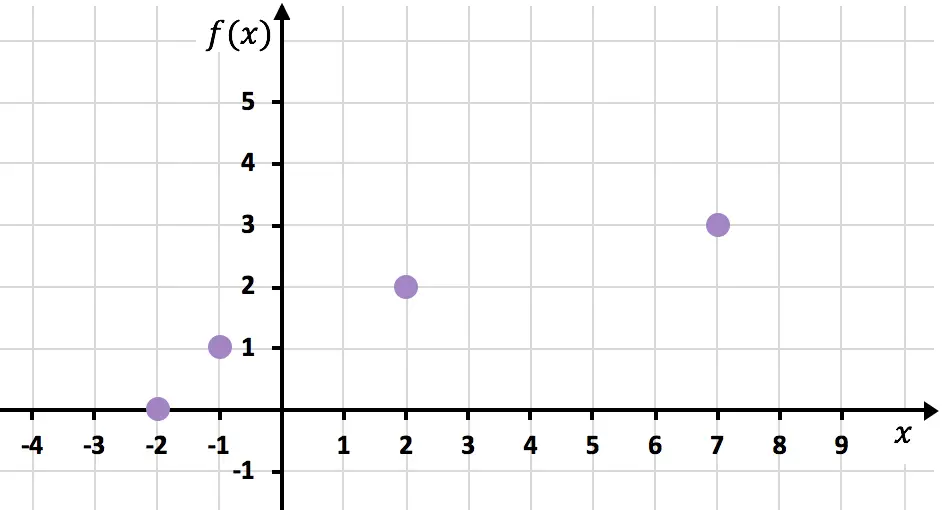
как представить радикальную или иррациональную функцию

И, наконец, мы соединяем точки и расширяем кривую, чтобы указать, что функция продолжает расти:

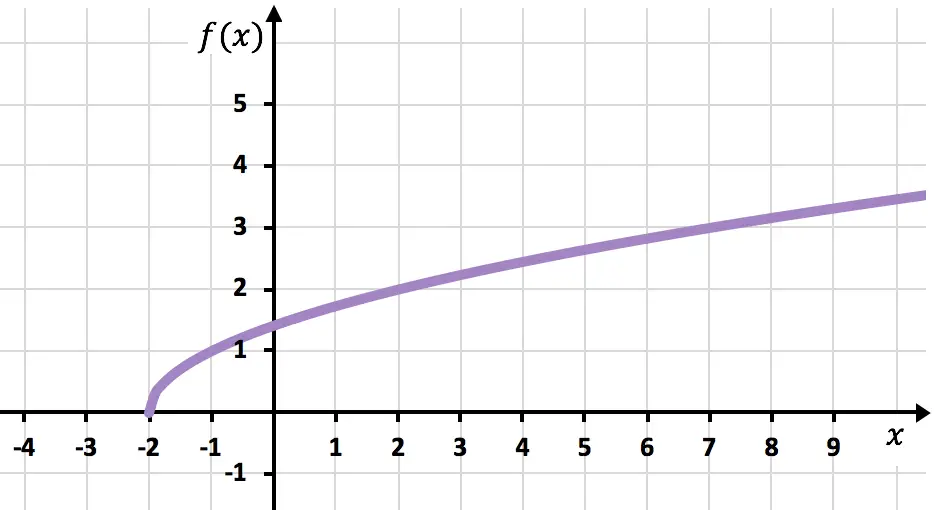
пример графического изображения радикальной или иррациональной функции

Решенные упражнения на иррациональные или радикальные функции

Упражнение 1

Найдите область определения следующей радикальной функции:

$\sqrt{3x+6}$

Посмотреть решение

Квадратного корня из отрицательного числа не существует. Следовательно, функция будет существовать, когда корневой аргумент положителен или равен нулю:

$3x+6 \ge 0$

$3x \ge -6$

$x \ge \cfrac{-6}{3}$

$x \ge -2$

$\mathbf{Dom } \ \bm{f = [-2,+\infty)}$

Упражнение 2

Найдите область определения следующей иррациональной функции:

$\sqrt{-x+2}$

Посмотреть решение

Квадратный корень из отрицательного числа не имеет реального решения. Следовательно, функция будет существовать до тех пор, пока содержимое корня положительно или равно нулю:

$-x+2\ge 0$

$-x\ge -2$

$x\le\cfrac{-2}{-1}=2$

Помните, что если в неравенстве мы меняем стороны отрицательного числа, которое умножается или делится, мы также должны повернуть знак неравенства.

$x\le2$

$\mathbf{Dom } \ \bm{f = (-\infty,2]}$

Упражнение 3

Постройте на графике следующую иррациональную функцию:

$f(x)= \sqrt{x-1}$

Посмотреть решение

Прежде всего, мы должны вычислить область определения функции:

$x-1\ge 0$

$x\ge 1$

$\text{Dom } f = [1,+\infty)$

Теперь создадим массив значений, задав значения функции в диапазоне доменов:

$x= 1 \ \longrightarrow \ f(1)= \sqrt{1-1}=0$

$x= 2 \ \longrightarrow \ f(2)= \sqrt{2-1}=1$

$x= 5 \ \longrightarrow \ f(5)= \sqrt{5-1}=2$

$x= 10 \ \longrightarrow \ f(10)= \sqrt{10-1}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 2 & 1 \\ 5 & 2 \\ 10 & 3 \end{array}$

Наконец, мы наносим точки и отображаем функцию на графике:

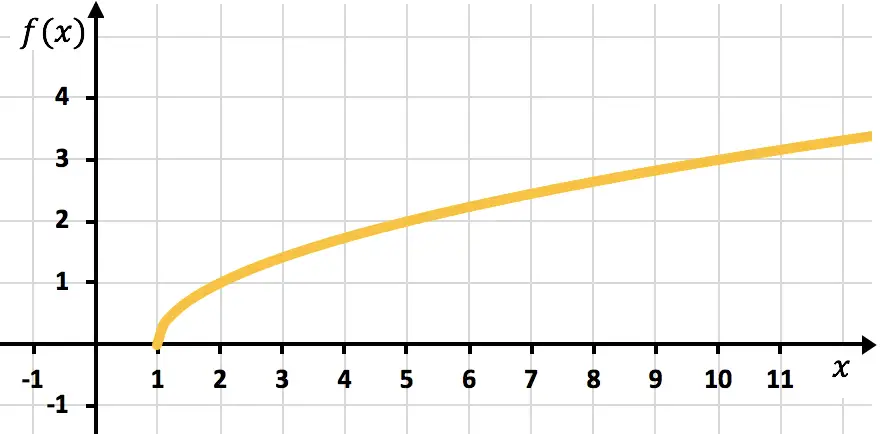
упражнение, решающее шаг за шагом иррациональную или радикальную функцию

Упражнение 4

Изобразите график следующей иррациональной или радикальной функции:

$f(x)= -2\sqrt{x}+3$

Посмотреть решение

Прежде всего, мы должны вычислить область определения функции:

$x\ge 0$

$\text{Dom } f = [0,+\infty)$

Теперь создадим массив значений, задав значения функции в диапазоне доменов:

$x= 0 \ \longrightarrow \ f(0)= -2\sqrt{0}+3=3$

$x= 1 \ \longrightarrow \ f(1)= -2\sqrt{1}+3=1$

$x= 4 \ \longrightarrow \ f(4)= -2\sqrt{4}+3=-1$

$x= 9 \ \longrightarrow \ f(9)= -2\sqrt{9}+3=-3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 3 \\ 1 & 1 \\ 4 & -1 \\ 9 & -3 \end{array}$

Наконец, наносим точки и рисуем функцию на графике:

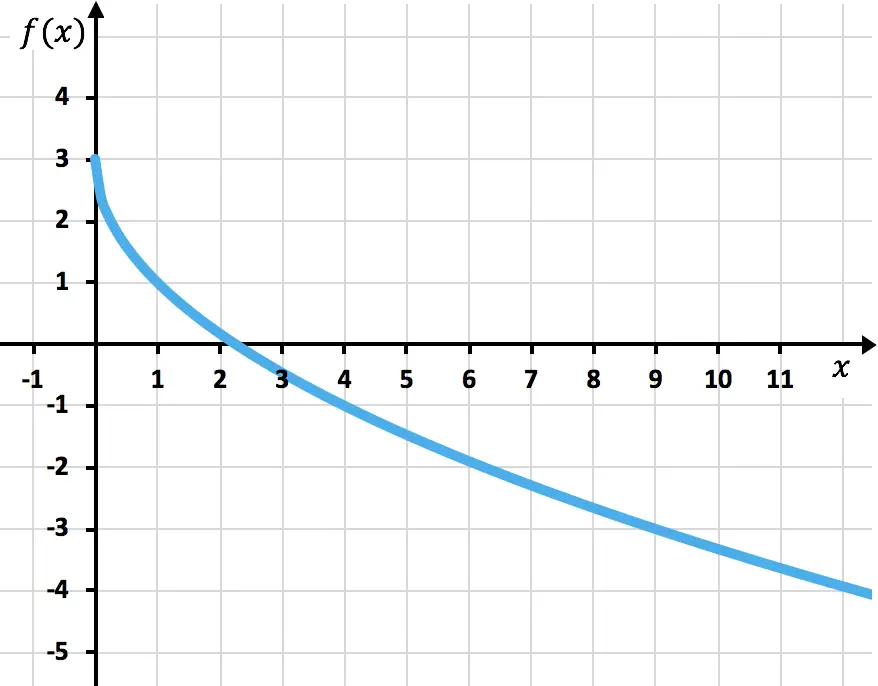
Упражнение 5

Изобразите график следующей иррациональной или радикальной функции:

$f(x)= \sqrt{-x+5}$

Посмотреть решение

Прежде чем построить график функции, нам необходимо вычислить область определения функции:

$-x+5\ge 0$

$-x\ge -5$

$x\le\cfrac{-5}{-1}=5$

Помните, что если в неравенстве мы меняем стороны отрицательного числа, которое умножается или делится, мы также должны изменить знак неравенства.

$x\le5$

$\text{Dom } f = (-\infty,5]$

Теперь построим таблицу значений, оценивая функцию в точках, принадлежащих области определения функции:

$x= 5 \ \longrightarrow \ f(5)=\sqrt{-5+5}=0$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{-4+5}=1$

$x= 1 \ \longrightarrow \ f(1)=\sqrt{-1+5}=2$

$x= -4 \ \longrightarrow \ f(-4)=\sqrt{-(-4)+5}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 5 & 0 \\ 4 & 1 \\ 1 & 2 \\ -4 & 3 \end{array}$

И, наконец, просто обозначаем точки и рисуем функцию на графике:

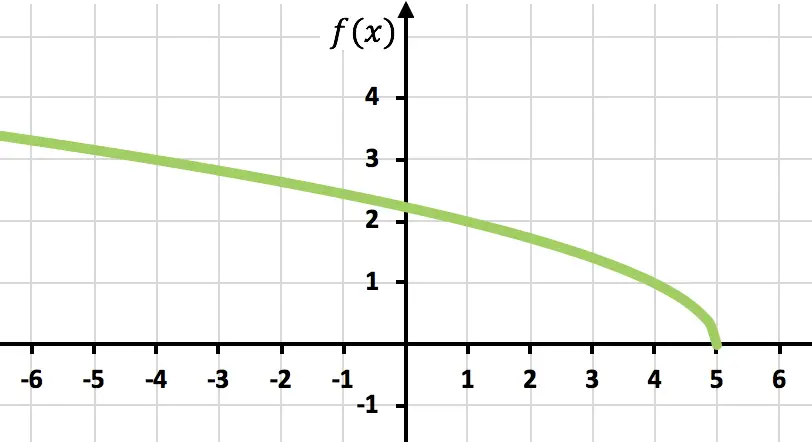
определенные упражнения радикальных или иррациональных функций

Упражнение 6

Постройте на графике следующую иррациональную или радикальную функцию:

$f(x)= \sqrt{x^2-5x+4}$

Посмотреть решение

Сначала мы должны вычислить область определения функции:

$x^2-5x+4\ge 0$

В данном случае мы получили неравенство второй степени, поэтому для его решения нужно применить формулу квадратных уравнений:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}$

Делим линию на три части с полученными корнями:

И подставляем число в каждый участок неравенства, чтобы увидеть, какие участки удовлетворяют неравенству и, следовательно, принадлежат области:

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=»Rendered by QuickLaTeX.com»> ❌ <p class=$ $x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 5}$

$5^2-5\cdot 5+4\ge 0 \ \longrightarrow \ 4\ge 0$

Таким образом, разделы, которые соблюдают неравенство, являются разделами сторон:

Таким образом, областью определения функции является:

$\text{Dom } f = (-\infty,1]\cup [4,+\infty)$

После того, как мы вычислили область определения функции, мы создаем таблицу значений, дающую значения функции в интервале области определения:

$x= 1 \ \longrightarrow \ f(1)=\sqrt{1^2-5\cdot 1+4} =0$

$x= 0 \ \longrightarrow \ f(0)=\sqrt{0^2-5\cdot 0+4} =2$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{(-1)^2-5\cdot (-1)+4} =3,16$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{4^2-5\cdot 4+4} =0$

$x= 5 \ \longrightarrow \ f(5)=\sqrt{5^2-5\cdot 5+4} =2$

$x= 6 \ \longrightarrow \ f(6)=\sqrt{6^2-5\cdot 6+4} =3,16$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 0 & 2 \\ -1 & 3,16 \\ 4 & 0 \\ 5 & 2 \\ 6 & 3,16 \\ \end{array}$

Наконец, представим полученные точки на графике и построим функцию:

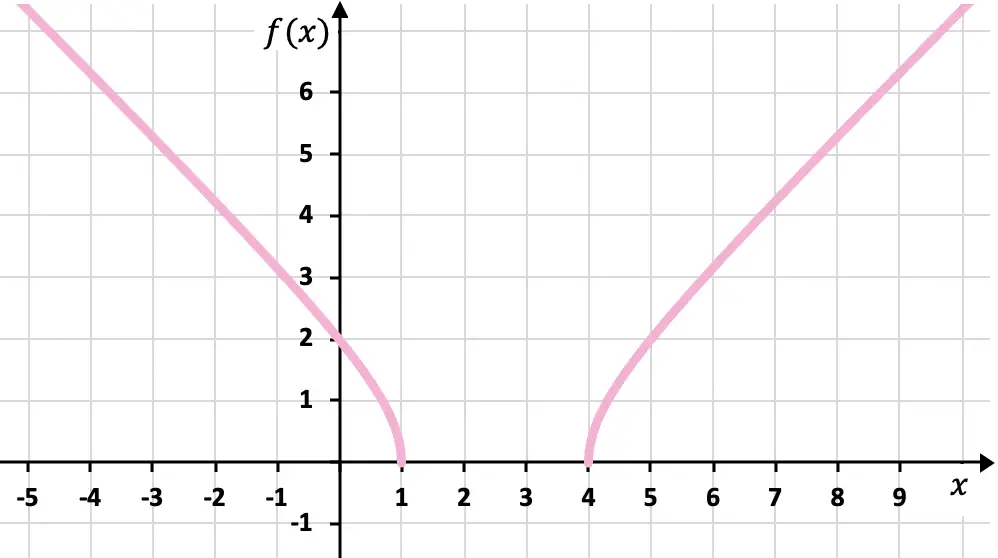
график иррациональной или радикальной функции с четным индексом

Упражнение 7

Представим на графике следующую функцию, образованную корнем:

$f(x)= \sqrt[3]{x}$

Посмотреть решение

Это иррациональная функция, корень которой имеет нечетный индекс, поэтому область определения функции состоит из действительных чисел:

$\text{Dom } f = \mathbb{R}$

Поэтому мы можем взять любую точку для создания таблицы значений. В этом случае мы будем искать много точек, потому что это кубический корень:

$x= 0 \ \longrightarrow \ f(0)= \sqrt[3]{0} = 0$

$x= 0,5 \ \longrightarrow \ f(0,5)= \sqrt[3]{0,5} = 0,79$

$x= -0,5 \ \longrightarrow \ f(-0,5)= \sqrt[3]{-0,5} = -0,79$

$x= 1 \ \longrightarrow \ f(1)= \sqrt[3]{1} = 1$

$x= -1 \ \longrightarrow \ f(-1)= \sqrt[3]{-1} = -1$

$x= 8 \ \longrightarrow \ f(8)= \sqrt[3]{8} = 2$

$x= -8 \ \longrightarrow \ f(-8)= \sqrt[3]{-8} = -2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 0 \\ 0,5 & 0,79 \\ -0,5 & -0,79 \\ 1 & 1 \\ -1 & -1 \\ 8 & 2 \\ -8 & -2 \end{array}$

Наконец, наносим найденные точки и строим функцию на графике:

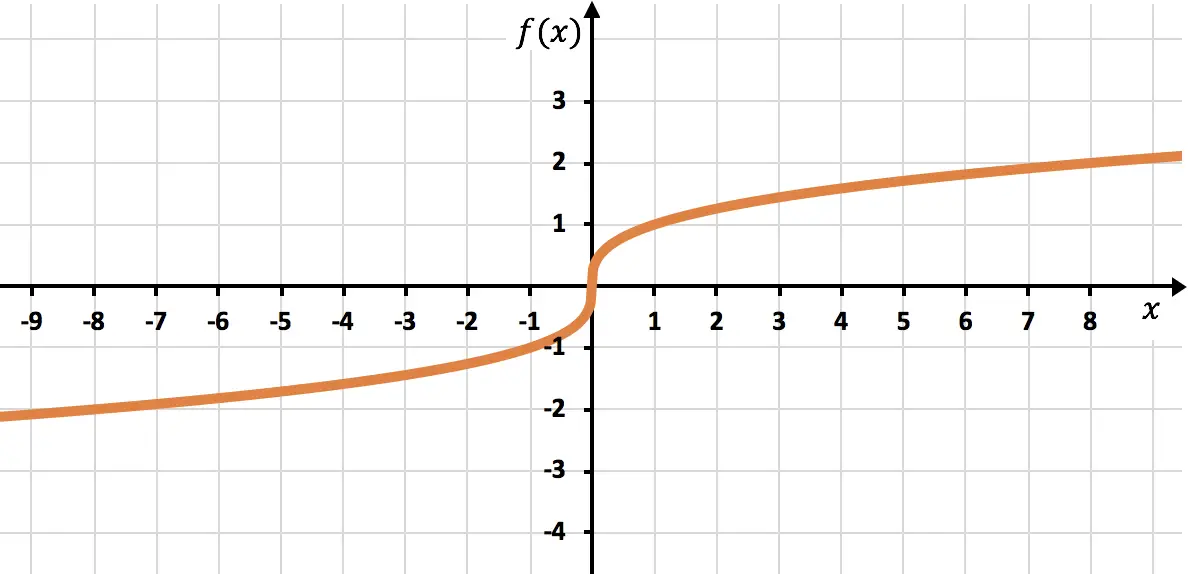
построить график иррациональной или радикальной функции с нечетным индексом

Упражнение 8

Решите следующую задачу, связанную с иррациональными (или радикальными) функциями:

Потребление аккумулятора сотового телефона определяется следующей функцией:

$f(t)=\sqrt{x-K \vphantom{(-K)}}$

Где потребление выражается в миллиамперах (мА) и

$t$

— прошедшее время в минутах.

Определить значение константы

$K$

так что через 4 минуты потребление составит 35 мА.

Посмотреть решение

То, что через 4 минуты потребление составляет 35 мА, означает, что когда t равно 4, f(t) равно 35. Таким образом, f(4)=35.

$f(4)=\sqrt{4-K} = 35$

$\sqrt{4-K} = 35$

Теперь нам нужно решить полученное уравнение. Если присмотреться, то это иррациональное уравнение, поскольку оно имеет корень. В уравнениях такого типа первое, что необходимо сделать, — это выделить корень одной стороны, которая в данном случае уже изолирована. После изоляции мы должны возвести в квадрат обе части уравнения:

$\left( \sqrt{4-K} \right)^2= 35^2$