Инволюционная матрица

На этой странице вы узнаете, что такое инволютивная матрица. Мы также покажем вам примеры инволютивных матриц размерностей 2×2, 3×3 и 4×4. И, наконец, вы найдете формулу инволюционной матрицы.

Что такое инволюционная матрица?

Смысл инволюционной матрицы следующий:

Определение инволютивной матрицы : Обратимая квадратная матрица, обратной матрицей которой является сама матрица.

$A^{-1} = A$

Золото

$A$

любая матрица и

$A^{-1}$

представляет собой его обратную сторону.

Итак, очевидно, что инволюционная матрица является примером регулярной или невырожденной матрицы .

Если вы не знаете, что такое обратная матрица, вы можете узнать здесь, как вычислить обратную матрицу 3х3 . Важно знать, как обратить матрицу, однако для этого нужно еще знать, как вычисляется сопряженная матрица .

Но вернемся к теме: когда матрица инволютивна, умножение матрицы на саму матрицу дает единичную матрицу. Взгляните на демо:

Любая матрица, умноженная на обратную, дает матрицу идентичности (или единицы измерения). ТАК:

$\displaystyle A \cdot A^{-1} = I$

А поскольку обратной инволюционной матрице является сама матрица:

$\displaystyle A \cdot A = I$

Следовательно, квадрат инволюционной матрицы дает единичную матрицу:

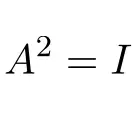
Примеры инволюционных матриц

Пример инволютивной матрицы 2×2:

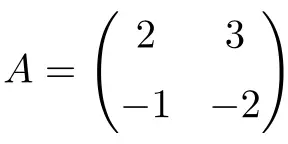
пример инволютивной матрицы размерности 2x2

Мы можем убедиться, что это инволюционная матрица, вычислив вторую степень матрицы:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Поскольку матрица A в квадрате является единичной матрицей, матрица A является инволюционной матрицей 2 × 2.

Пример инволюционной матрицы 3×3:

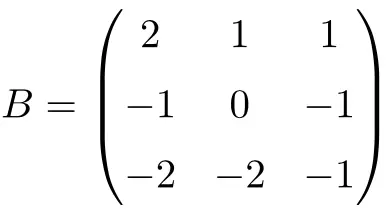
пример инволютивной матрицы размерности 3x3

Мы можем убедиться, что это инволюционная матрица, решив произведение матрицы на себя:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Поскольку матрица B в квадрате является единичной матрицей, матрица B представляет собой инволюционную матрицу размером 3 × 3.

Пример инволютивной матрицы 4×4:

Матрица идентичности (или единицы измерения), независимо от ее размера, по определению является инволюционной матрицей.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Мы можем убедиться, что это инволюционная матрица, увеличив ее до 2:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Поскольку квадрат единичной матрици является единичной матрицей, единичная матрица представляет собой инволюционную матрицу 4×4.

Очевидно, единичная матрица может иметь любую размерность, поскольку это просто диагональная матрица со всеми единицами на главной диагонали и остатком 0. Таким образом, единичная матрица всегда будет инволюционной матрицей, независимо от ее порядка.

Формула инволюционной матрицы

Одним из свойств инволюционной матрицы является то, что ее формула может быть известна. Но доказательство формулы для инволюционной матрицы второго порядка довольно утомительно, поэтому оставим вас сразу к результату, вот что действительно важно. Если вас больше интересует демо-версия, вы можете увидеть ее пошаговое объяснение ниже в комментариях.

Формула инволютивной матрицы размерности 2 × 2 выглядит следующим образом:

Следовательно, любая матрица, у которой значения главных диагоналей противоположны и определитель которой равен -1, будет инволюционной матрицей.

Однако помимо матриц, описываемых этой формулой, необходимо учитывать, что единичная матрица и ее противоположность также являются инволюционными матрицами второго порядка:

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

Свойства инволютивной матрицы

Инволюционные матрицы обладают следующими характеристиками:

Определитель инволюционной матрицы всегда равен -1 или +1.

Существует связь между инволюционными матрицами и идемпотентными матрицами : матрица
$A$

инволюционна тогда и только тогда, когда матрица

$\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$

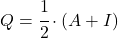
является идемпотентным.

Ага
$A$

И

$B$

две коммутирующие инволюционные матрицы, то матричное произведение

$AB$

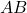
также является еще одной инволюционной матрицей.

Любая степень инволюционной матрицы приводит к другой инволюционной матрице. В частности, инволюционная матрица, возведенная в нечетный показатель, будет равна сама себе, с другой стороны, если она возведена в четный показатель, она будет эквивалентна матрице идентичности.

$A^2 = I$

$A^3 = A$