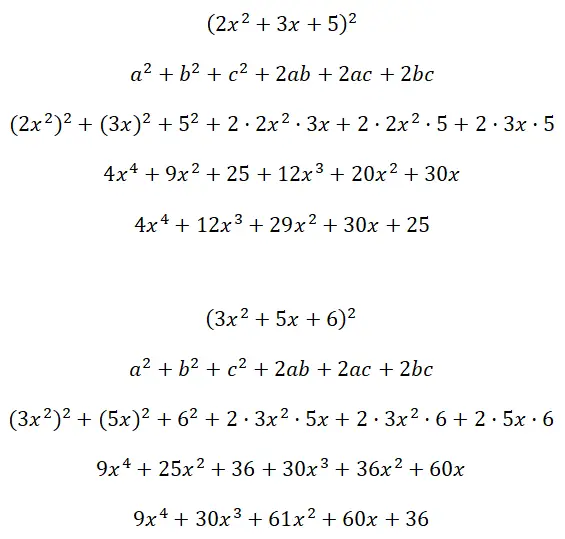Что такое выдающиеся продукты или выдающиеся личности?
Замечательные тождества , также называемые замечательными произведениями или замечательными равенствами , представляют собой математические ресурсы, которые позволяют быстрее решать произведения и частные многочленов . Как указывает слово «идентичность», это равенства, которые позволяют нам вычислять эти операции без необходимости их решения. Поскольку мы знаем, что это выражение подчиняется фиксированным правилам (которые всегда соблюдаются), и, следовательно, мы можем получить результат без необходимости его проверки.
Когда использовать заметную индивидуальность?
Эти тождества в основном используются в области алгебры, и их основная функция — ускорить решение определенного полинома без необходимости решать всю операцию целиком. Оттуда мы получаем формулы известных продуктов, которые мы будем комментировать на протяжении всей статьи. И, наконец, мы можем применять формулы к полным квадратам, факторным полиномам или любому другому типу вычислений.
Как шаг за шагом решить замечательное изделие?
Чтобы распознать заметные личности, вам нужно выполнить очень простую процедуру, которая также имеет большой смысл:
- Определите тип заметной идентичности. Первым шагом является определение типа операции: заметный продукт или заметный коэффициент. Вам также следует уточнить, какой тип формулы вам нужно будет применить, хотя вы поймете это позже, когда мы объясним различные типы заметных личностей.
- Примените формулу: как только вы узнаете, какую формулу вам нужно применить, пришло время выполнить расчеты. В зависимости от типа тождества вам придется решать более или менее сложные операции и в подавляющем большинстве случаев эти вычисления будут состоять из термов, содержащих хотя бы одно неизвестное.
- Упростите выражение: Наконец, когда вы получите результат, вам нужно его упростить. На этом этапе вам необходимо сгруппировать похожие термины и упорядочить их, чтобы сформировать хорошо структурированный результирующий многочлен. Следует отметить, что этот шаг так же важен, как и остальные, поскольку в противном случае упражнение останется незавершенным.
Формулы известных личностей или основных известных продуктов
Ниже вы найдете все формулы, соответствующие известным тождествам. В дополнение к теоретическому объяснению каждого случая есть также несколько примечательных примеров решенных продуктов, благодаря которым вы лучше поймете все концепции. Стоит отметить, что в этом первом разделе вы найдете только самые важные личности . Но, прочитав эту статью, вы узнаете, как разрабатывать более сложные и заметные продукты, например, состоящие из трехчленов.
квадрат суммы
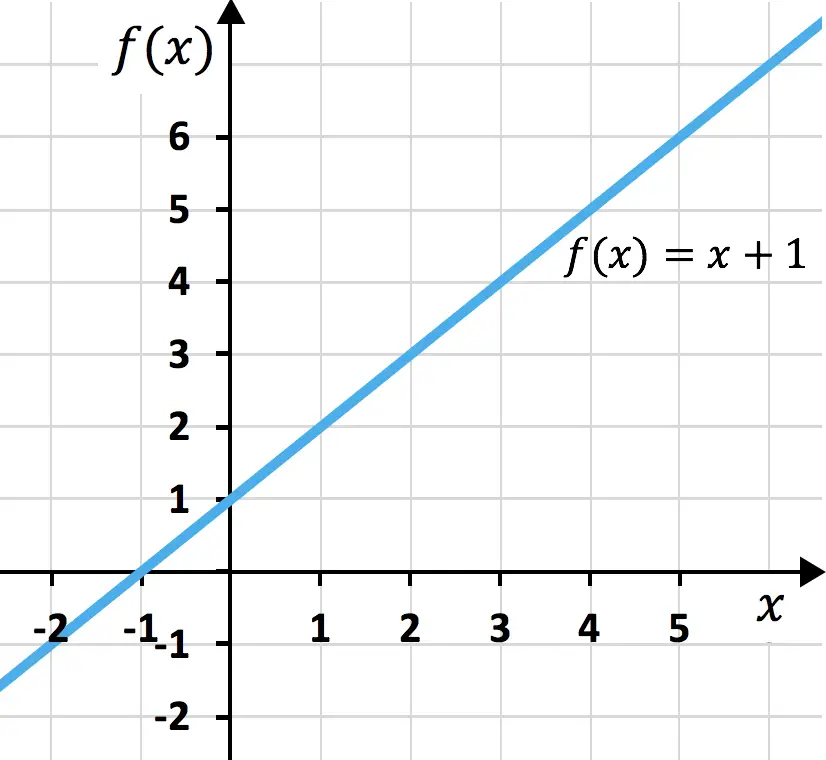
Первый случай касается квадрата суммы , который является очень распространенным полиномиальным выражением в мире алгебры. Это можно найти в виде: (a + b) 2 , что эквивалентно: (a + b) · (a + b). Следовательно, мы знаем, что ее можно решить с помощью полиномиального умножения. Но, благодаря примечательным тождествам, мы можем сэкономить время, воспользовавшись следующей формулой: (a + b) 2 = a 2 + 2ab + b 2 . Далее мы покажем вам демонстрацию формулы , которую мы только что видели, таким образом вы сможете понять, откуда она взялась и как она используется:
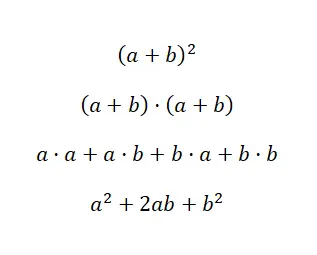
Как мы видим, проверку мы провели с помощью умножения полиномов, о котором мы ранее комментировали. И можно со стопроцентной уверенностью сказать, что если знать полученную формулу наизусть, то, выполнив простую подстановку значений , можно получить результат быстрее. Так что это очень полезная математическая концепция. Теперь, когда вы знаете, как работает квадрат суммы, мы покажем вам конкретный пример:
Пример квадрата суммы
Вычислите примечательное тождество (2x + 4) 2 :
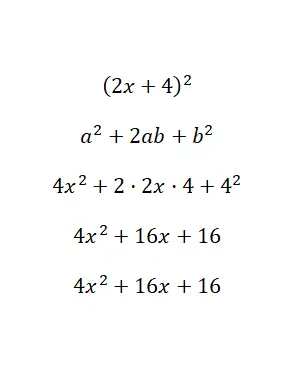
По сути, мы связали значения бинома с буквами формулы и решили: a = 2x и b = 4. Наконец, после решения всех вычислений, мы получаем многочлен 4x 2 + 16x + 16, который равен эквивалентен оригиналу . В этом примере мы получили расширенный полином (в стандартной форме) из приведенного полинома.
квадрат вычитания
Еще одно очень распространенное выражение — квадрат вычитания , который во многом похож на квадрат сложения, только меняется на один знак. Тогда структура бинома эквивалентна: (a – b) 2 , и если мы его развернем, получим: (a – b) · (a – b). Как и в предыдущем случае, это можно вычислить путем умножения многочленов, хотя и здесь есть формула, облегчающая решение: a 2 – 2ab +b 2 . Ниже вы можете найти эмпирическое подтверждение этого:
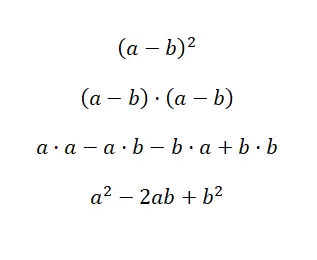
Чтобы упростить определение квадрата разности, мы можем использовать ту же формулу, которую мы использовали для суммы квадратов, но с отрицательным первым знаком . Это минимальное изменение позволяет адаптировать выражение к биномам, состоящим из положительного и отрицательного членов, что полезно для вычитаний. Теперь мы покажем вам решенный пример:
Пример квадрата вычитания
Вычислите заметное тождество (x – 3) 2 :
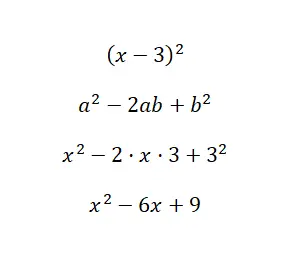
Как вы можете видеть в примере решения, мы подставили значения нашего бинома в формулу a = x и b = 3. Таким образом, используя формулу, которую мы объяснили ранее, мы получили только замену и некоторые очень простые действия. расчеты. Это позволяет нам увидеть, насколько легко с помощью этого выражения можно вычислить квадрат разницы.
Разность квадратов или сумма по разности
Третий случай примечательных произведений называется разностью квадратов , он образуется произведением положительного бинома и отрицательного бинома. Выражение этого стиля имеет следующую структуру: (a + b) · (a – b), поэтому, если разложить это произведение, мы получим формулу, облегчающую расчет: a 2 – b 2 . Как видите, это очень простая формула, хотя для полного ее понимания необходимо разработать все расчеты:
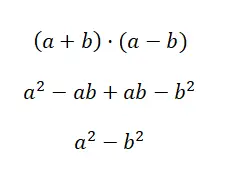
Пример суммы по разнице
Вычислите примечательное тождество (x + 1) · (x – 4):
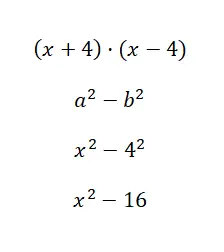
В этом случае численный расчет очень прост, фактически нам нужно было найти только степень. Хотя правда, эта формула применима только тогда, когда биномы имеют один и тот же главный член и один и тот же независимый член, но с измененным знаком. Итак, эта идентичность важна, но вы не будете использовать ее чаще всего.
Произведение двух биномов с общим членом
В этом четвертом случае мы сталкиваемся с ситуацией, очень похожей на предыдущую, хотя и с небольшим изменением структуры. Обратите внимание на разницу, которую мы вам покажем: (x + a) · (x + b) и (a + b) · (a – b). Если вам это все еще не совсем ясно, рассмотрим следующий пример: (x + 4) · (x + 5) и (x + 4) · (x – 4). В первом случае ( произведение двух общих биномов терминов ) существует только один общий термин, а во втором случае (сумма по разности) два члена являются общими, но независимый член имеет обратный знак. Тем не менее, давайте посмотрим, по какой формуле мы можем действовать:
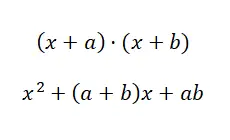
Пример произведения двух биномов с общим членом
Найдите примечательное произведение (x + 2) · (x + 3):
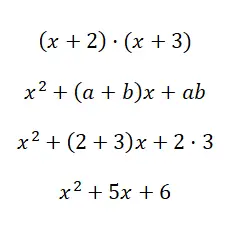
Используя формулу x 2 + (a + b)x + ab, мы можем вычислить полином второй степени, полученный в результате умножения двух биномов. Мы надеемся, что на этом примере вы поняли разницу между двумя последними случаями, которые мы объяснили, потому что иногда их бывает сложно различить.
квадрат трехчлена
Когда мы пытаемся вычислить квадрат трехчлена, мы также получаем замечательный результат, который облегчает нашу жизнь. Это выражение представляется следующим образом: (a + b + c) 2 и эквивалентное произведение: a 2 + b 2 + c 2 + 2ab + 2ac + 2bc. Следует отметить, что это справедливо в случае положительного трехчлена, но если один из коэффициентов отрицательный, нужно просто вписать в формулу отрицательное значение. Ниже приведена демонстрация формулы:
Пример квадрата трехчлена
Вычислите примечательное тождество (2x + 1 + x 2 ) 2 :
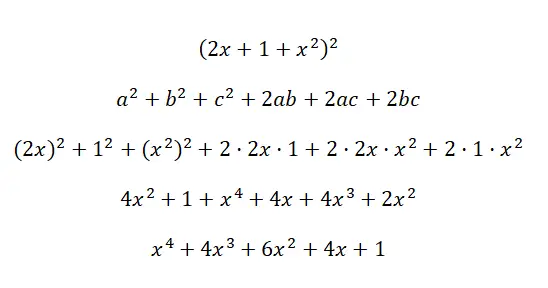
Замечательные формулы идентичности или замечательные кубические произведения
Теперь, когда мы объяснили основные известные тождества, мы рассмотрим их производные , начиная с куба биномов. Чтобы рассчитать примечательные продукты этого стиля, нам придется прибегнуть к формулам, которые немного более сложны, но имеют структуру, аналогичную тем, которые мы уже обсуждали.
биномиальный куб
Куб бинома записывается: (a + b) 3 и (a – b) 3 , это выражение эквивалентно следующей формуле: (a 3 + 3a 2 b + 3ab 2 + b 3 ), и (a 3 – 3а 2 б + 3аб 2 – б 3 ). Эти два случая называются кубом суммы и кубом вычитания, поскольку они представляют собой кубы биномов. Ниже вы найдете очень подробную демонстрацию каждого случая:
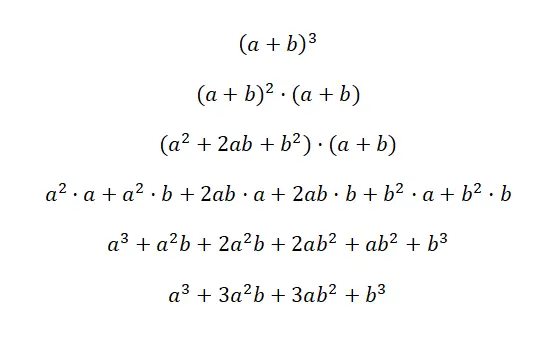
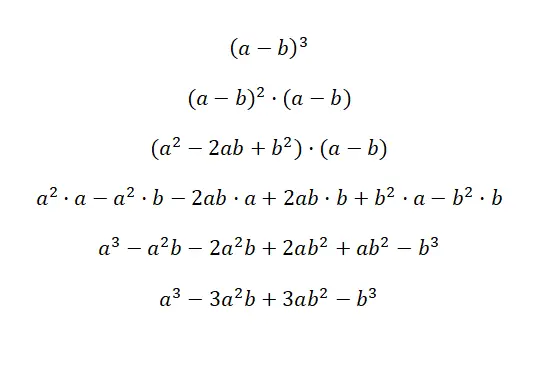
Ключом к пониманию этого первого доказательства является понимание того, что (a + b) 3 эквивалентно: (a + b) 2 · (a + b). Таким образом, мы используем формулу квадрата суммы , которую мы объяснили ранее, для умножения другого коэффициента. Тогда мы просто упростим выражение и получим соответствующее примечательное тождество: a 3 + 3a 2 b + 3ab 2 + b 3 . В случае второго примера происходит то же самое, но со сменой знака.
Пример биномиального куба
Решите примечательное тождество (x + 3) 3 :
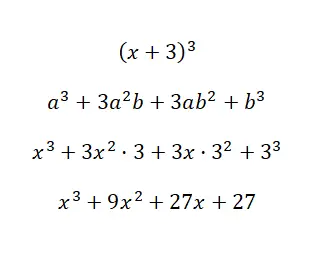
Используя формулу, которую мы только что обсудили, мы можем вычислить полином, принимая во внимание, что: a = xyb = 3. Как видите, процедура очень проста и не имеет особых сложностей при расчете, все потому, что у нас есть формула . В противном случае выполнение такого большого количества умножений было бы довольно утомительным.
Сумма кубов и разность кубов
У нас есть еще один случай, который легко спутать с предыдущим. Хотя эти два случая написаны по-разному, они не эквивалентны. Выражение, эквивалентное сумме или разности кубов, имеет вид: a 3 + b 3 , тогда как в предыдущем случае мы говорили о: (a + b) 3 . Как видите, в структуре выражения есть неоспоримое сходство, но на самом деле, когда дело доходит до построения расчета, это два совершенно разных случая:
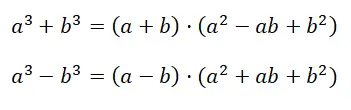
При демонстрации формулы мы получаем факторизацию первого многочлена , именно мы идем от исходного бинома к произведению бинома на трехчлен. Кажется, что полученный результат (a + b) · (a 2 – ab + b 2 ), совершенно не упрощает расчет, но на самом деле, факторизируя многочлен, мы получаем выражение, которое очень легко понять.
Пример суммы кубов
Вычисляем знатное произведение х 3 +27:
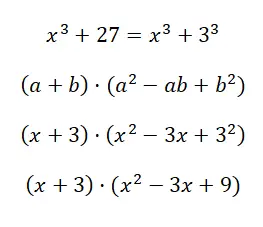
В этом случае результат мы получим довольно длинный, потому что его нельзя упростить дальше. Но прийти к такому выражению вполне нормально, ведь в этих случаях можно получить только результат со структурой, эквивалентной произведению бинома на трёхчлен, как в этом примере.
трехчлен в кубе
Куб трехчлена записывается: (a + b + c) 3 , что представляет собой умножение трех одинаковых трехчленов, но без показателя степени: (a + b + c) · (a + b + c) · (a + b +в). Это самый сложный заметный продукт, хотя формула вполне логична и получается так же, как и все остальные, при выполнении соответствующих умножений многочленов. Ниже вы найдете доказательство формулы этого замечательного тождества:
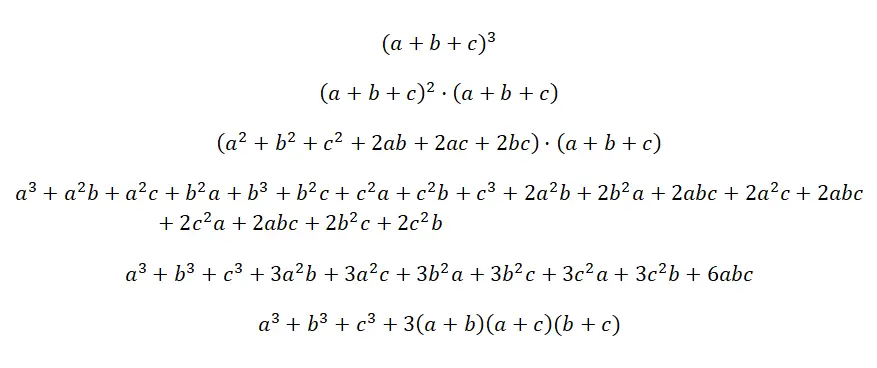
Пример куба трехчлена
Решите следующий трёхчленный куб (x 2 + 3x – 4) 3 :
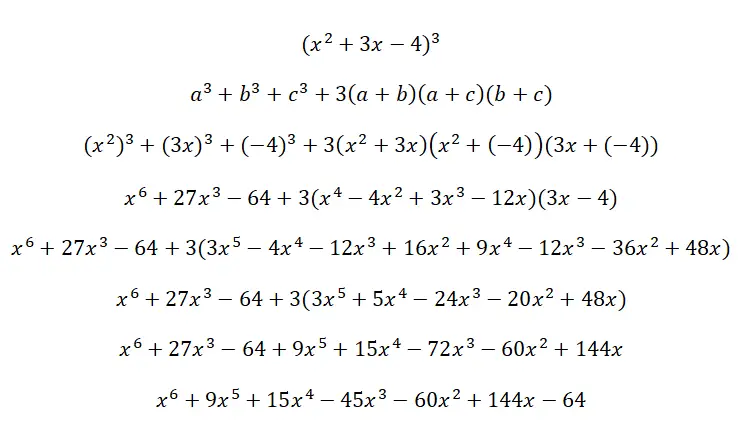
замечательные соотношения
Наконец, мы объясним примечательные факторы , которые являются примечательными тождествами для быстрого решения определенных типов алгебраических дробей. Точнее, существует четыре разных типа, которые имеют одну общую характеристику: их результат состоит из точных полиномов (с остатком, равным нулю). Стоит также отметить, что формулы замечательных частных имеют определенную связь с формулами замечательных продуктов, которые мы уже объяснили.
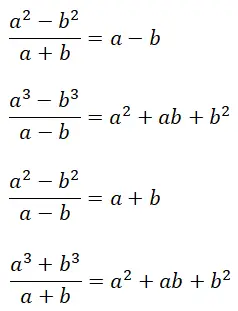
Пример решения замечательных соотношений
Рассчитайте следующие заметные соотношения:
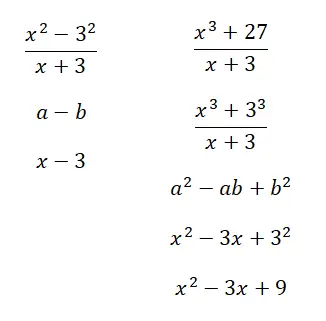
Решены замечательные упражнения с продуктом
Теперь, когда вы знаете, как решаются различные важные задачи, пришло время немного попрактиковаться. Вот почему мы предлагаем вам 6 упражнений для применения всей изложенной теории. А мы покажем вам таблицу основных примечательных тождеств, чтобы она была у вас под рукой, пока вы решаете все упражнения:

Упражнение 1
Решите биномиальные квадраты (x – 4) 2 , (x + 1) 2 и (x – 3) 2 :
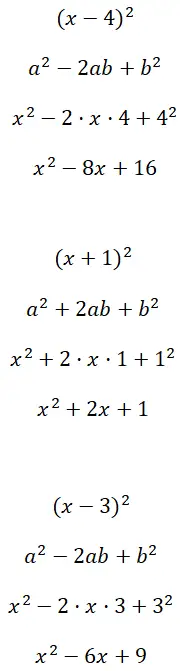
Упражнение 2
Вычислите две разности квадратов (x – 1) · (x + 1) и (x + 3) · (x – 3):
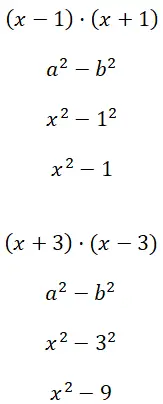
Упражнение 3
Разложим примечательные произведения в куб (x – 5) 3 и (x + 8) 3 :
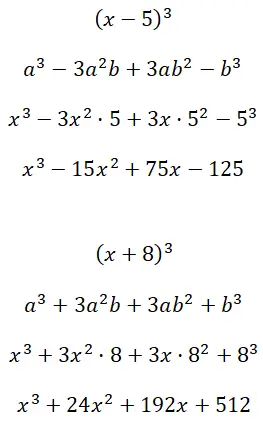
Упражнение 4
Разработайте заметные тождества, образованные из многофакторных термов (4x 2 + 5y) 2 , (5x 3 + y 2 ) · (5x 3 – y 2 ) и (5xy 2 – 2xy) 2 :
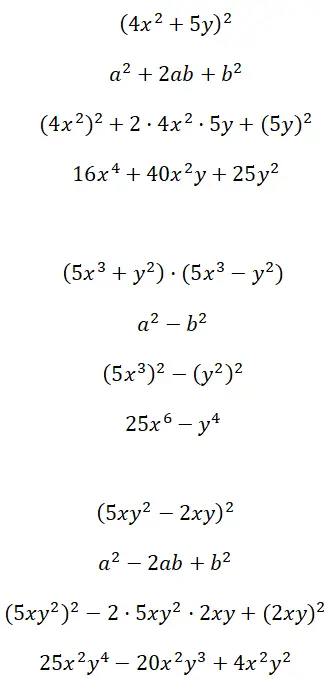
Упражнение 5
Вычислите значимые кубические произведения, образованные многофакторными членами (3x 2 + y) 3 и (5y 3 – 2x 2 ) 3 :
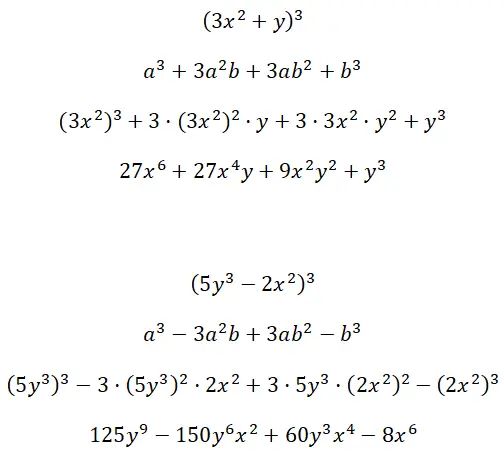
Упражнение 6
Решите квадраты трёхчленов ( 2×2 +3x+5) 2 и ( 3×2 +5x+6):