Дроби или смешанные числа — это числовые выражения, обозначающие одну величину, разделенную на другую. Следовательно, это значение представляет собой частное двух чисел. С помощью этого типа чисел мы можем выражать десятичные и целые величины и даже указывать пропорции . Далее мы определим дроби более математически и покажем вам несколько примеров, чтобы вы поняли эту концепцию графически.
Что такое дроби?
Дробь равна количеству частей, которые мы извлекаем из единицы, разделенной на равные части. Итак, графически он представлен двумя терминами, разделенными горизонтальной линией посередине. Точнее, вверху строки находим числитель, а внизу знаменатель.
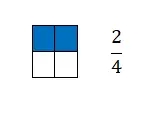
Как видите, дроби — это очень простая математическая концепция для графического отображения, поскольку они идут рука об руку с пропорциями. Именно поэтому в предыдущем примере мы выразили количество цветных квадратов дробным числом.
Дробные члены
Две части дроби:
- Числитель: этот член расположен над горизонтальной линией, и здесь мы пишем количество взятых нами кусочков. Мы можем найти положительные, отрицательные и нулевые (равные нулю) числители.
- Знаменатель: этот другой термин расположен под чертой, и здесь мы записываем общее количество частей, на которые разделена единица. Мы можем найти положительные и отрицательные знаменатели, но они не могут быть равны нулю.
виды дробей
Существует много видов дробей, в зависимости от чисел, из которых они состоят, и эквивалентности, которую они представляют с другими дробями. Далее мы определим все существующие категории и прокомментируем характеристики, которые позволяют их отличать от других:
- Правильные дроби: это те, у которых числитель меньше знаменателя. Если преобразовать эти дроби в десятичные , то получится число от нуля до единицы. Оно не может быть больше единицы, поскольку значение числителя всегда будет меньше значения знаменателя и, следовательно, единица не будет превышена.
- Неправильные дроби: это те, у которых числитель больше знаменателя, в этом случае они выражают числовые значения, большие единицы. Например, 8/5 равно 1,6, что больше 1. Это еще один способ выражения смешанных чисел следующего типа.
- Смешанные дроби: также называемые смешанными числами, это те, которые состоят из целого числа и смешанного числа. В основном они представлены целым значением перед дробью, поэтому, чтобы преобразовать их в неправильные дроби, вам нужно умножить целую часть на знаменатель, прибавить ее к числителю и оставить знаменатель прежним.
- Десятичные дроби: это те, у которых знаменатель выражает величину, эквивалентную десятичной степени, например: 6/10, 34/1000 или 5/100. Они используются в десятичной записи и наиболее распространены при преобразовании точных десятичных чисел в смешанные числа. Мы обсудим это более подробно в следующем разделе.
- Сложные дроби: это те, которые состоят из другой дроби либо в числителе, либо в знаменателе, либо в обоих. Итак, чтобы упростить эти выражения и представить их в виде одной дроби, нам нужно разделить числитель на знаменатель. Это станет яснее, когда мы объясним деление дробей.
- Эквивалентные дроби: это те, которые эквивалентны одному и тому же числу, хотя и не состоят из одинаковых числителей и знаменателей. Например, 8/4 = 4/2 = 2, обе дроби равны двум. В данном конкретном случае это связано с тем, что первая дробь в два раза равна второй, поэтому сохраняется пропорциональное соотношение.
- Несократимые дроби: это те дроби, которые невозможно упростить дальше, поскольку числитель и знаменатель не имеют общих множителей и, следовательно, не могут делиться ни на какое число. Некоторые примеры этого типа: 9/5, 5/6, 7/8 и другие. Чтобы знать, как их обнаружить, важно уметь вычислять наибольший общий делитель .
Операции с дробями
Теперь, когда мы знаем различные существующие категории дробей, мы увидим, как решать различные арифметические операции со смешанными числами . Следует отметить, что это немного сложнее, чем операции с целыми числами, хотя, как только вы поймете методологию, все будет довольно просто. Более того, мы не только объясним теорию, но и покажем вам несколько примеров. С учетом сказанного, давайте начнем.
сумма дробей
Складывать дроби с общим знаменателем довольно просто, поскольку вы просто складываете два числителя, а знаменатель оставляете прежним. С другой стороны, сложение дробей с разными знаменателями становится немного сложнее, потому что вам нужно найти наименьшее общее кратное знаменателей. А затем мы должны сложить произведение каждого числителя, разделив lcm (новый знаменатель) на старый знаменатель. Для лучшего понимания можно посмотреть на следующую схему:
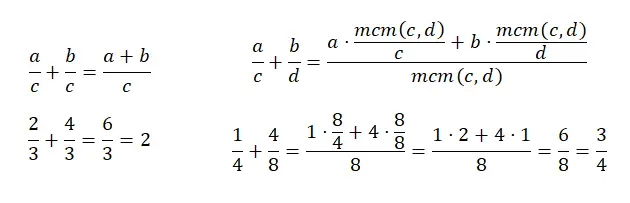
дроби вычитания
Вычитание дробей с общим знаменателем очень похоже на сложение, по сути все делается так же, за исключением суммы числителей, ведь вместо сложения приходится вычитать. И при вычитании дробей с разными знаменателями происходит то же самое, практически то же самое, только вместо того, чтобы складывать произведение числителей путем деления н.к.м. на старый знаменатель, надо вычитать . Вот еще одна диаграмма:
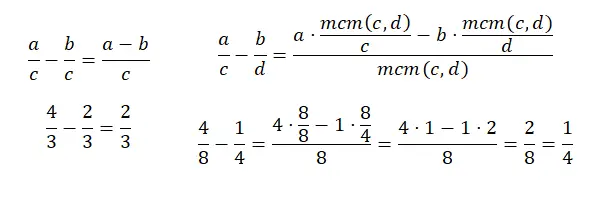
умножение дробей
Умножение дробей можно решить одинаково, независимо от того, одинаковые знаменатели или нет. По сути, вам нужно умножить числители на одну часть, а знаменатели на другую. Это, пожалуй, самая простая операция, поскольку вам нужно выполнить всего два умножения.
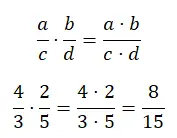
деление дробей
Деление на дроби тоже решить довольно легко, нужно всего лишь перемножить крестики. Другими словами, числитель — это результат умножения числителя первой дроби на знаменатель второй. тогда как знаменатель представляет собой произведение знаменателя первой дроби и числителя второй.
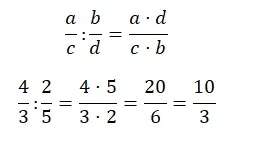
Упростить дроби
Упрощение дробей или сокращение дробей не является арифметической операцией как таковой, но очень важно знать, как это делать, а также это тема, которую мы уже немного касались видов дробей. Итак, чтобы упростить смешанное число, нам нужно разделить числитель и знаменатель на одно и то же число. Обычно для такого упрощения мы выбираем наибольший общий фактор . На следующем изображении вы можете найти пример.
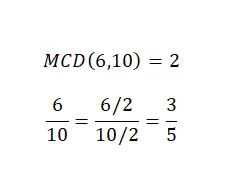
Как видите, у нас есть две эквивалентные дроби , поэтому обе представляют одно и то же числовое значение, но вторая проще первой. Таким образом, мы успешно достигли цели упрощения.
Как перейти от десятичной дроби к дробной и наоборот?
Производящая дробь — это несократимая дробь, полученная из десятичного числа, либо точного десятичного числа, либо повторяющегося десятичного числа. Конечно, нам придется использовать разные методы в зависимости от типа десятичной дроби, о которой мы поговорим ниже.
Преобразование точной десятичной дроби в производящую дробь
В этом случае мы можем прибегнуть к десятичным дробям , о которых мы говорили вначале. Проще говоря, нам нужно в числителе записать числовое значение, но без десятичной точки. А в знаменателе пишем степень десяти, у которой нулей столько, сколько цифр в числителе.
Однако если у нас есть десятичное число больше единицы, например 4,25, тогда нам нужно будет умножить количество имеющихся у нас полных единиц на значение знаменателя и прибавить его к исходному числителю. Ниже вы найдете примеры каждого типа:
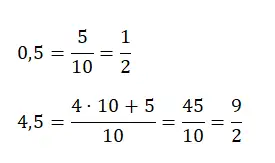
Преобразование чистой повторяющейся десятичной дроби в порождающую дробь
Когда у нас есть чистое периодическое десятичное число , если мы хотим получить производящую дробь, нам придется поставить в числитель то же значение, но без десятичной точки и вычесть целую часть. Хотя знаменатель будет равен числу, состоящему только из девяток, мы должны конкретно записать столько девяток, сколько цифр в десятичной части исходного числа. Эта система несколько запутанна, но на нескольких примерах мы поймем:
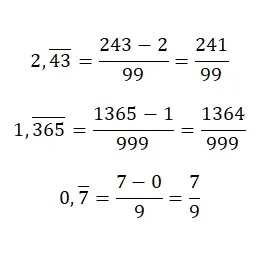
Преобразование смешанных повторяющихся десятичных дробей в генерирующие дроби
В случае наличия смешанного повторяющегося десятичного числа нам придется применить довольно сложное правило. Сначала мы запишем число без запятой в числителе и вычтем целую часть, за которой следуют неповторяющиеся десятичные дроби, также без запятой. Что касается знаменателя, вам нужно будет написать столько девяток, сколько цифр в периодической десятичной части, а затем столько нулей, сколько цифр в неповторяющейся десятичной части.
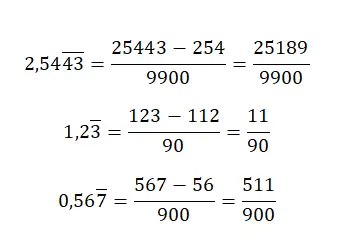
перевести дробь в десятичную
Чтобы перейти от дроби к десятичной, просто разделите числитель на знаменатель, поскольку смешанное число — это не что иное, как частное между двумя значениями . Итак, решив деление, вы получите соответствующее десятичное число. На следующем изображении вы можете найти несколько довольно простых примеров:
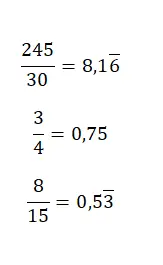
упражнения с дробями
Теперь, когда вы знаете всю теорию о дробях, мы рекомендуем вам выполнить несколько упражнений. Таким образом, вы изучите все концепции, объясненные более подробно, и в день экзамена вы быстрее решите вычисления. Кроме того, вы видели все существующие типы упражнений с дробями и будете знать, как их решать соответствующим образом. Наконец, позвольте мне сообщить вам, что у нас также есть в вашем распоряжении онлайн- калькулятор дробей , с помощью которого вы можете решать все операции с дробями.