Диагональная матрица

На этой странице вы увидите, что такое диагональная матрица и примеры диагональных матриц. Кроме того, вы узнаете, как работать с матрицами такого типа, как легко вычислять их определители и как их инвертировать. Также есть свойства и применения диагональных матриц. И, наконец, есть объяснения двудиагональной и трехдиагональной матриц.

Что такое диагональная матрица?

Диагональная матрица — это квадратная матрица, в которой все элементы, не входящие в главную диагональ, равны нулю (0). Элементы главной диагонали могут быть нулевыми, а могут и не быть нулевыми.

Как только мы узнаем точное определение диагональной матрицы, мы увидим примеры диагональных матриц:

Примеры диагональных матриц

Пример диагональной матрицы размерности 2 × 2

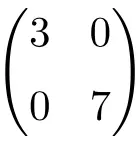
Пример диагональной матрицы порядка 3×3

Пример диагональной матрицы размером 4×4

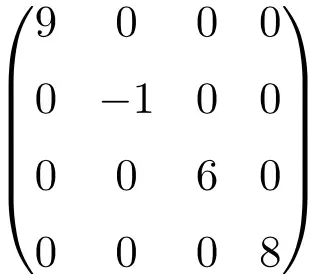
Матрицы такого типа обычно записываются с указанием элементов диагонали:

$diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Операции с диагональными матрицами

Одна из причин, по которой диагональные матрицы так важны для линейной алгебры, заключается в простоте, с которой они позволяют выполнять вычисления. Вот почему они так используются в математике.

Сложение и вычитание диагональных матриц

Складывать (и вычитать) две диагональные матрицы очень просто: достаточно сложить (или вычесть) числа на диагоналях.

$\displaystyle \text{diag}(a_1,... ,a_n) \pm \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\pm b_1,..., a_n\pm b_n)$

Например:

$\displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}$

Умножение диагональной матрицы

Чтобы решить задачу умножения или матричного произведения двух диагональных матриц, просто умножьте элементы диагоналей вместе.

$\displaystyle \text{diag}(a_1,... ,a_n) \cdot \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\cdot b_1,..., a_n\cdot b_n)$

Например:

$\displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}$

Степень диагональных матриц

Чтобы вычислить степень диагональной матрицы, нам нужно возвести каждый элемент диагонали в показатель степени:

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle A^k= \text{diag}(a_1^k,... ,a_n^k)$

Например:

$\displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}$

Определитель диагональной матрицы

Определителем диагональной матрицы является произведение элементов главной диагонали.

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle \text{det}(A)= \prod_{i =1}^n a_i$

Посмотрите на следующее решенное упражнение, в котором мы находим определитель диагональной матрицы, просто умножая элементы ее главной диагонали:

$\displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30$

Эту теорему легко доказать: нужно просто вычислить определитель диагональной матрицы по блокам (или сомножителям). Эта демонстрация подробно описана ниже с использованием общей диагональной матрицы:

$\begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}$

Перевернуть диагональную матрицу

Диагональная матрица обратима тогда и только тогда, когда все элементы главной диагонали отличны от 0 . В этом случае мы говорим, что диагональная матрица является регулярной матрицей.

Кроме того, обратная диагональной матрице всегда будет другой диагональной матрицей с обратной основной диагональю:

$\displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}$

Из предыдущей характеристики можно сделать вывод, что определитель обратной диагональной матрицы является произведением обратных главной диагонали:

$\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}$

$\displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{4} \cdot \cfrac{1}{-1}=-\cfrac{1}{8} = -0,125$

Свойства диагональных матриц

Любая диагональная матрица также является симметричной матрицей .

Диагональная матрица — это матрица, имеющая одновременно верхнюю и нижнюю треугольную форму .

Единичная матрица представляет собой диагональную матрицу:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Аналогично, нулевая матрица также является диагональной матрицей, поскольку все ее элементы, не находящиеся на диагонали, являются нулями. Хотя цифры по диагонали — 0.

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Собственные значения (или собственные значения) диагональной матрицы — это элементы ее главной диагонали.

$\begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7$

Квадратная матрица является диагональной тогда и только тогда, когда она треугольная и нормальная .

Сопряженным к диагональной матрице является другая диагональная матрица.

Приложения с диагональной матрицей

Как мы видели, решать вычисления с диагональными матрицами очень просто, поскольку в операциях участвует много нулей. По этой причине они очень полезны в области математики и широко используются.

По этой же причине было проведено так много исследований о том, как диагонализировать матрицу , и даже был разработан метод диагонализации матриц (с использованием характеристического многочлена).

Поэтому диагонализуемые матрицы также весьма актуальны. Как теорема о спектральном разложении, которая устанавливает условия, когда матрица может быть диагонализирована, а когда нет.

двудиагональная матрица

Двудиагональная матрица — это квадратная матрица, в которой все элементы, не находящиеся на главной диагонали или на верхней или нижней диагонали, равны 0.

Например:

$\begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}$

верхняя двудиагональная матрица

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}$

нижняя двудиагональная матрица

Когда главная диагональ и первая супердиагональ заняты, мы говорим о верхней двудиагональной матрице. С другой стороны, когда главная диагональ и первая поддиагональ заняты, мы говорим о нижней двудиагональной матрице.

трехдиагональная матрица

Трехдиагональная матрица — это квадратная матрица, единственными ненулевыми элементами которой являются элементы главной диагонали и соседних диагоналей сверху и снизу.

Например:

$\begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}$

Таким образом, все диагональные, двудиагональные и трехдиагональные матрицы являются примерами ленточных матриц . Потому что ленточная матрица — это та матрица, у которой все ненулевые элементы расположены вокруг главной диагонали.

Что такое диагональная матрица?

Примеры диагональных матриц

Операции с диагональными матрицами

Сложение и вычитание диагональных матриц

Умножение диагональной матрицы

Степень диагональных матриц

Определитель диагональной матрицы

Перевернуть диагональную матрицу

Свойства диагональных матриц

Приложения с диагональной матрицей

двудиагональная матрица

трехдиагональная матрица

Оставьте комментарий Отменить ответ