▷ Как делить многочлены (решенные упражнения)

На этой странице вы узнаете, как делить многочлены: как деление многочлена на моном, так и деление многочлена на другой многочлен. Вы также сможете увидеть примеры деления многочленов и попрактиковаться с пошаговыми решениями упражнений. А кроме того, вы узнаете свойства этой полиномиальной операции.

Полиномиальное (или полиномиальное) деление

Прежде чем мы увидим, как именно делятся два многочлена, мы кратко рассмотрим концепции деления многочлена, чтобы потом было легче понять метод, который мы собираемся использовать.

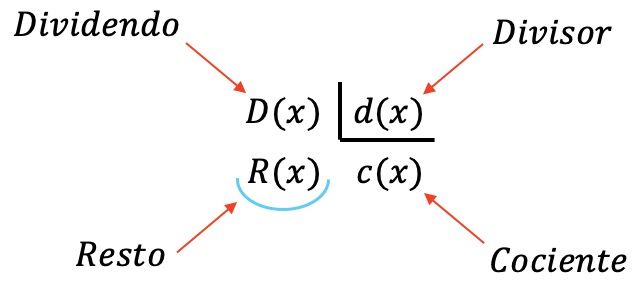
В полиномиальном делении участвуют четыре многочлена:

Дивиденд : разделенный полином.
Делитель : полином, который делит делимое.
Частное : результат деления делимого на делитель.
Остаток (или остаток): полином, оставшийся при делении двух полиномов.

С другой стороны, вы также должны знать, что между многочленами есть два типа деления:

Точное деление многочленов : деление между многочленами является точным, когда остаток равен нулю. В этом случае делимое полинома равно делителю, умноженному на частное.

$D(x)=d(x) \cdot c(x)$

Более того, в этом случае дивиденд

$D(x)$

кратно делителю

$d(x)$

и частное

$c(x).$

Аналогично, полиномиальный делитель и полиномиальное частное являются делителями делимого.

Целочисленное деление многочленов : при целочисленном (или неточном) делении многочленов остаток ненулевой (0). Тогда выполняется фундаментальное свойство полиномиального деления:

$D(x)=d(x) \cdot c(x) + R(x)$

Теперь, когда мы увидели, что такое деление многочленов, давайте посмотрим, как делить многочлены друг на друга. Точнее, мы сначала объясним деление между многочленом и мономом, а затем деление между двумя многочленами.

Деление многочлена на моном

Прежде чем посмотреть, как разделить многочлен на моном, давайте сначала вспомним, как делятся между собой мономы, так как это необходимо знать, чтобы иметь возможность проделать этот тип полиномиальной операции.

Деление двух одночленов предполагает деление их коэффициентов между собой и буквенных частей друг с другом, т. е. делятся коэффициенты мономов и вычитаются показатели степеней переменных, имеющих одинаковое основание. Посмотрите на следующий пример:

$12x^5: 3x^2 = \cfrac{12x^5}{3x^2}=(12:3) x^{5-2} = 4x^3$

Теперь посмотрим, что включает в себя деление многочлена на моном:

В математике, чтобы решить деление многочлена на моном, каждый член многочлена делится на моном.

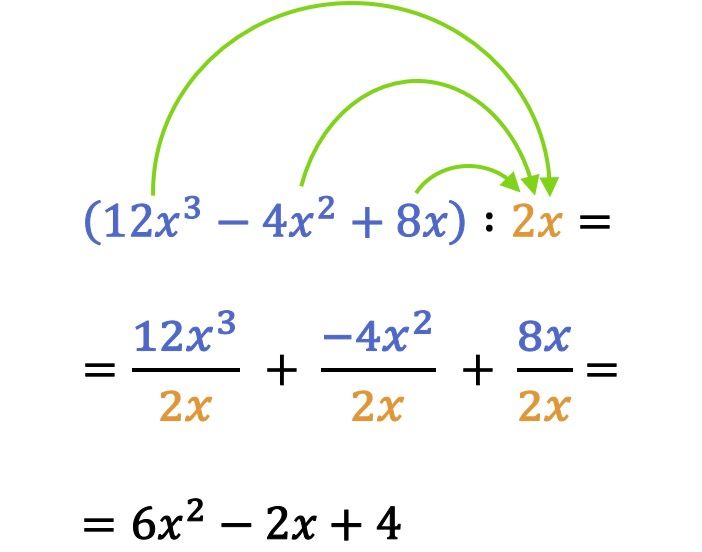
Обратите внимание, что в предыдущем примере деления при делении мономов или многочленов также необходимо учитывать правило знаков. Фактически, очень распространенная ошибка при делении полиномов на мономы заключается в неправильном понимании знака члена.

Деление многочлена на другой многочлен

Чтобы разделить два многочлена, необходимо выполнить определенную процедуру, поэтому давайте посмотрим, как выглядит метод деления многочленов, также называемый делением многочленов в длину, пошагово решая пример:

Вычислить результат деления многочлена
$P(x)$

между полиномом

$Q(x).$

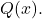
Будучи двумя полиномами:

$P(x) =x^3+4x^2+12 \qquad \qquad Q(x) =x-4$

$\cfrac{P(x)}{Q(x)} = \ ?$

Первое, что нужно сделать, это привести полиномы к форме деления. Слева пишем числитель дроби (делимый полином), а справа ставим знаменатель дроби (делительный полином):

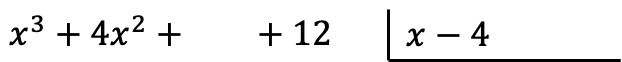
Внимание: если в многочлене нет монома определенной степени, на его месте необходимо оставить пробел. Например, полином

$x^3+4x^2+12$

Срок первого года обучения отсутствует, поэтому вместо него остается пустое место.

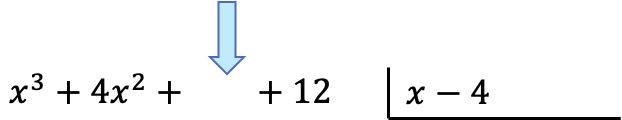
деление многочленов при отсутствии члена

Получив полиномы, мы найдем частное. И чтобы найти первый член частного, мы должны разделить первый член делимого на первый член делителя:

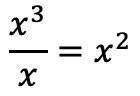
И вместо частного ставим результат деления:

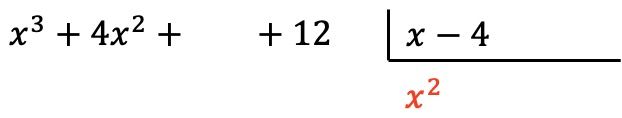
Теперь умножаем найденный член на каждый элемент делителя, и каждый результат помещаем под делимым в соответствующем столбце , меняя его знак :

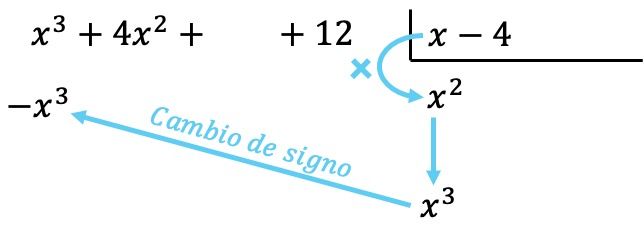
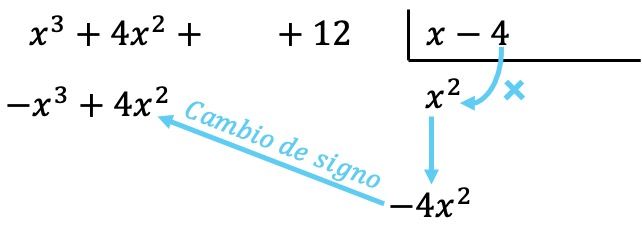
Как и во всех операциях с многочленами, важно упорядочить многочлены от высшей степени к низшей, чтобы все члены одной степени находились в одном столбце.

После того, как мы разместили результаты умножения с противоположным знаком, нам нужно добавить члены, выровненные по вертикали:

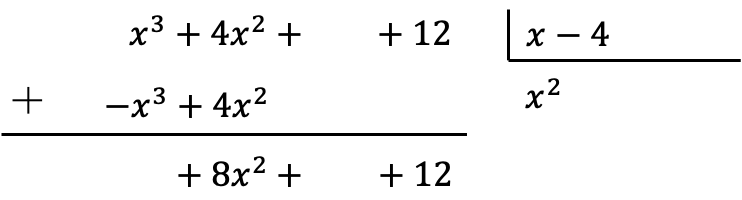
Обратите внимание, что при выполнении этой суммы коэффициент с наивысшей степенью сокращается, и, следовательно, у нас на один член меньше в дивиденде.

Теперь нам нужно повторять ту же процедуру до тех пор, пока делимое полинома не станет на одну степень меньше делителя полинома.

Поэтому мы делим первый член делимого на первый член делителя:

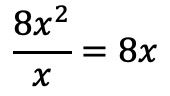
Помещаем результат в частное:

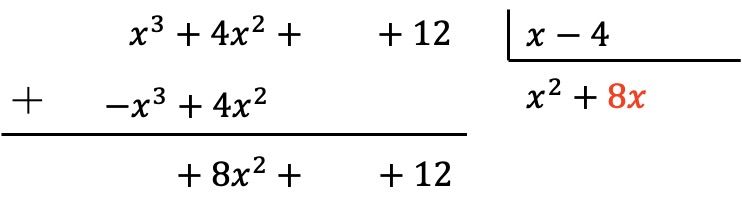
Как и прежде, умножаем новый член частного на каждый элемент делителя и помещаем результаты противоположного знака в соответствующие столбцы делимого:

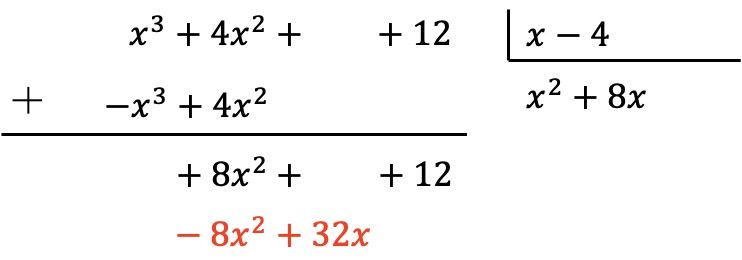
И добавляем вертикально:

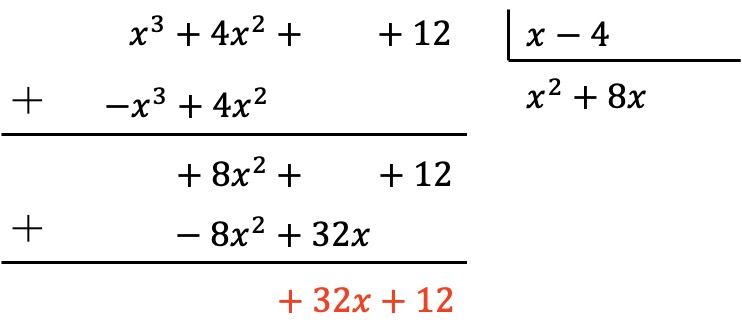
Полином делимого по-прежнему ни на одну степень меньше полинома делителя, поэтому нам нужно продолжать делать тот же процесс.

Итак, сначала мы делим первый член дивиденда на первый член делителя, затем умножаем результат на каждый член делителя, затем ставим измененные результаты под знак делимого и, наконец, складываем по вертикали:

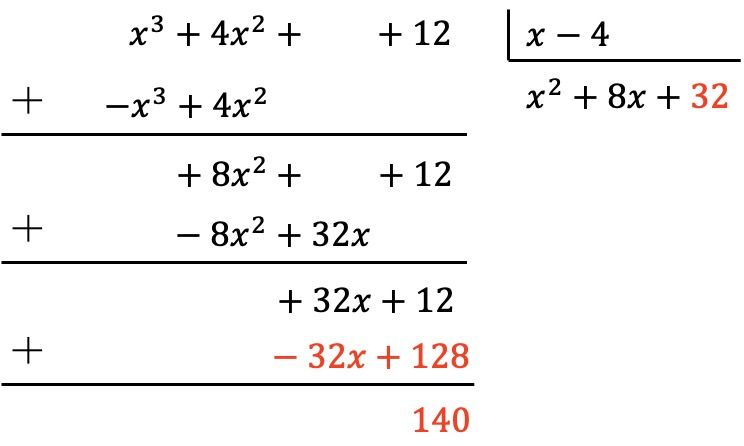
Итак, мы уже получили, что полином делимого имеет степень меньшую, чем степень делителя, потому что делимое имеет степень 0, а делитель имеет степень 1. Следовательно, деление завершено.

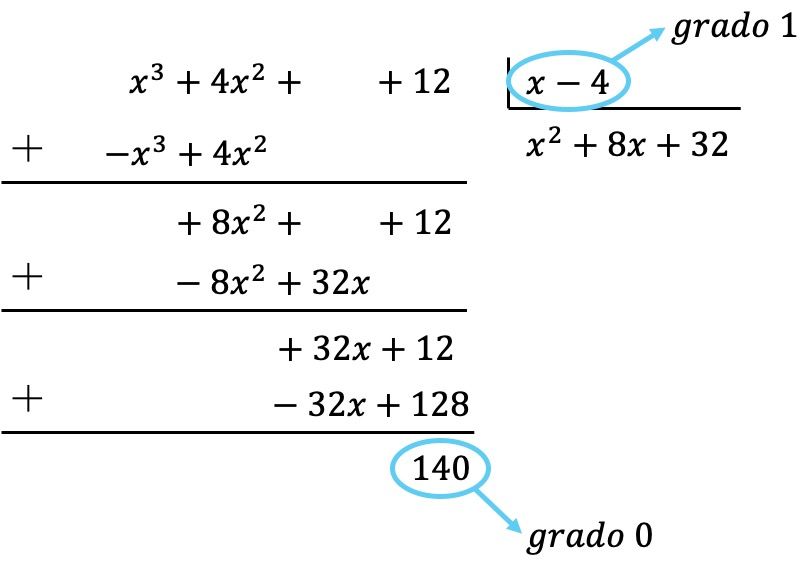
Таким образом, результатом деления будет:

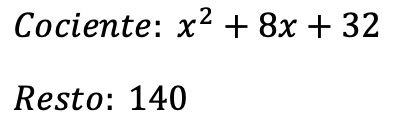
С другой стороны, мы можем проверить, правильно ли мы выполнили деление полинома, основываясь на фундаментальном условии деления многочленов:

$D(x)=d(x) \cdot c(x) + R(x)$

$x^3+4x^2+12=(x-4) \cdot (x^2+8x+32) + 140$

$x^3+4x^2+12=x^3+8x^2+32x-4x^2-32x-128+ 140$

$x^3+4x^2+12=x^3+4x^2+12$

✅

Уравнение удовлетворяется, значит, деление полинома выполнено правильно.

Итак, мы закончили деление многочленов и надеемся, что смогли помочь вам с этим объяснением. Что вы думаете о методе деления многочленов? У вас есть сомнения? Вам это нравится? Или вы бы предпочли, чтобы полиномиальных делений не существовало? 😂 Читаем вас в комментариях! 👇👇👇

Свойства делящих многочленов

Любое деление полиномов отвечает следующим характеристикам:

✓ Степень полиномиального делимого всегда должна быть больше степени полиномиального делителя.

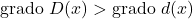$\text{grado } D(x) >\text{grado } d(x)» title=»Rendered by QuickLaTeX.com» height=»19″ width=»193″ style=»vertical-align: -5px;»></p> </p> <p> <strong><span style=$ ✓ Степень полиномиального делимого эквивалентна сумме степеней делителя и частного.

$\text{grado } D(x) =\text{grado } d(x)+\text{grado } c(x)$

✓ Степень остатка всегда меньше степени делителя (а значит, и делимого).

$\text{grado } R(x) <\text{grado } d(x)$

✓ Делимое равно произведению делителя на частное плюс остаток. Это условие ставится и при делении чисел.

$D(x)=d(x) \cdot c(x) + R(x)$

Решенные упражнения на деление многочленов

Упражнение 1

Определите результат следующего деления многочлена на моном:

$\left(15x^5+9x^3 \right) : \left(3x^2\right)$

Посмотреть решение

Чтобы разделить многочлен на моном, необходимо решить деление каждого члена многочлена на указанный моном:

$\begin{aligned} \left(15x^5+9x^3 \right) : \left(3x^2\right) & = \cfrac{15x^{5}}{3x^2}+ \cfrac{9x^3}{3x^2} \\[2ex] & = \bm{5x^3+3x} \end{aligned}$

Помните, что при делении между одночленами коэффициенты делятся между собой и вычитаются показатели степеней, у которых основание одинаковое.

Упражнение 2

Вычислите следующее деление многочлена на моном:

$\left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right)$

Посмотреть решение

Чтобы разделить многочлен на моном, необходимо разделить каждый член многочлена на указанный моном:

$\begin{aligned} \left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right) & = \cfrac{16x^5}{4x^2}+ \cfrac{-4x^3}{4x^2} + \cfrac{-20x^2}{4x^2} \\[2ex] & = \bm{4x^3-x-5} \end{aligned}$

Помните, что при мономиальном делении коэффициенты делятся между собой и вычитаются показатели степеней с эквивалентным основанием.

Упражнение 3

Решите следующее деление многочлена на моном:

$\left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right)$

Посмотреть решение

Чтобы разделить многочлен на моном, необходимо решить деление каждого члена многочлена на указанный моном:

$\begin{aligned} \left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right) & = \cfrac{12x^{10}}{-6x^3}+ \cfrac{-30x^{7}}{-6x^3} + \cfrac{-18x^6}{-6x^3} + \cfrac{54x^4}{-6x^3} \\[2ex] & = \bm{-2x^7+5x^4+3x^3-9x} \end{aligned}$

Имейте в виду, что делящий одночлен отрицательный, поэтому знаки всех делений меняются.

Упражнение 4

Выполним следующее деление многочленов:

$\cfrac{x^4+x^3-x^2+x+1}{x^3-5}$

Посмотреть решение

Чтобы разделить полиномы, вы должны применить метод, описанный выше:

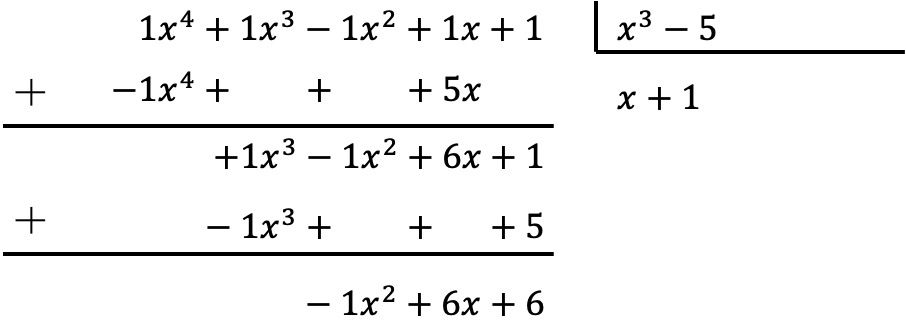
Таким образом, результатом деления двух полиномов будет:

Коэффициент:

$x+1$

Отдых:

$-x^2+6x+6$

Упражнение 5

Вычислите следующее деление многочленов:

$\cfrac{2x^3-3x^2-5x-5}{x-2}$

Посмотреть решение

Чтобы решить деление многочлена на бином, мы должны применить метод, который мы видели выше:

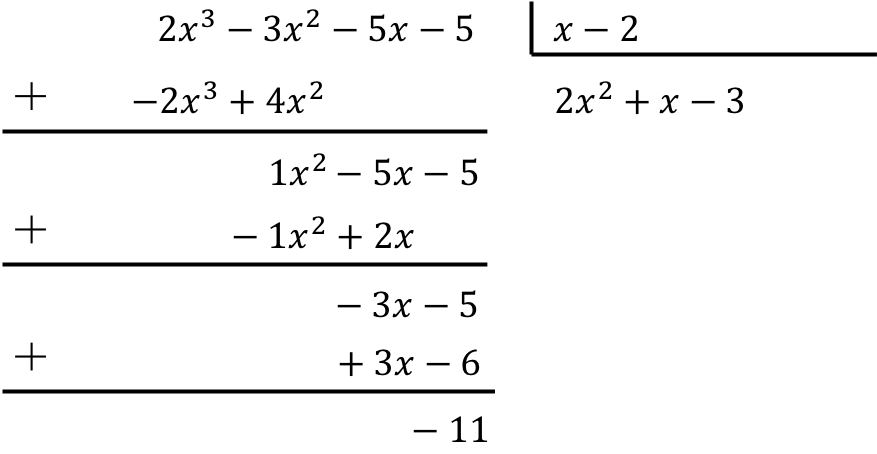
пошагово решенные упражнения на деление многочленов

Таким образом, результатом полиномиального деления будет:

Коэффициент:

$2x^2+x-3$

Отдых:

$-11$

Упражнение 6

Решите следующее деление многочленов:

$\cfrac{x^4+x^2+3}{x^3+3x^2+2x}$

Посмотреть решение

Чтобы вычислить деление многочленов, мы должны применить объясненный метод:

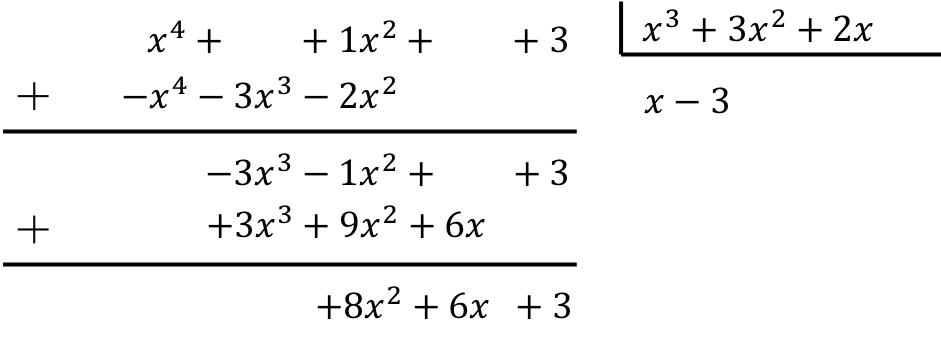
Таким образом, результатом деления двух полиномов будет:

Коэффициент:

$x-3$

Отдых:

$8x^2+6x+3$

Упражнение 7

Найдите результат следующего деления двух полиномов:

$\cfrac{x^4-2x^3+x^2-x-3}{x^2+x+1}$

Посмотреть решение

Чтобы вычислить деление многочлена на трехчлен, вы должны применить описанный метод:

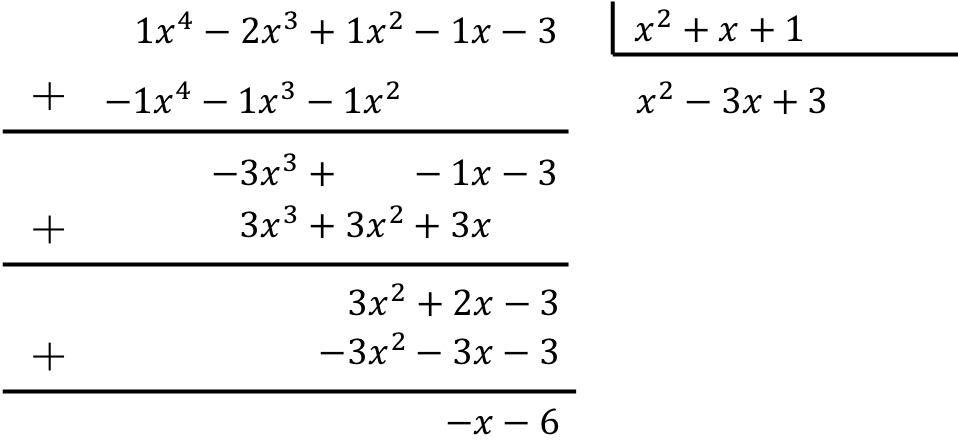
упражнения решены шаг за шагом на деление многочленов

Таким образом, результатом деления двух полиномов будет:

Коэффициент:

$x^2-3x+3$

Отдых:

$-x-6$

👉👉👉Если вы зашли так далеко, значит, вы уже знаете, как делятся многочлены. Яркий! Теперь, когда вы освоили деление многочленов, знайте, что существует метод, позволяющий гораздо быстрее решать определенные задачи деления между многочленами . Это синтетическое деление или правило Руффини , посмотреть, как применяется этот трюк и когда его можно использовать, можно, перейдя по ссылке.😉

Полиномиальное деление

Полиномиальное (или полиномиальное) деление

Деление многочлена на моном

Деление многочлена на другой многочлен

Свойства делящих многочленов

Решенные упражнения на деление многочленов

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Упражнение 6

Упражнение 7

Оставьте комментарий Отменить ответ