Гиперболическая производная арксинуса

Здесь вы найдете, что является производной гиперболического арксинуса (формула). Кроме того, вы сможете увидеть несколько упражнений, решаемых на производные гиперболического арксинуса функции. Наконец, мы покажем вам формулу производной тригонометрической функции этого типа.

Формула гиперболической производной арксинуса

Производная гиперболического арксинуса x равна единице по квадратному корню из x в квадрате плюс 1.

f(x)=\text{arcsenh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2+1}}

Таким образом , производная гиперболического арксинуса функции равна частному производной этой функции, деленному на квадратный корень этой функции, возведенный в квадрат плюс один.

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

Вторая формула аналогична первой, но с применением правила цепочки. То есть по первой формуле можно вывести только гиперболический арксинус xy, тогда как по второй формуле можно вывести гиперболический арксинус любой функции.

полученный из гиперболического арксинуса

Имейте в виду, что гиперболический арксинус — это обратная функция гиперболического синуса, производную которого вы можете увидеть здесь:

➤ См.: формула производной гиперболического синуса

Примеры гиперболической производной арксинуса

Пример 1

f(x)=\text{arcsenh}(3x)

Чтобы найти производную функции арксинуса, мы используем формулу, показанную выше:

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

Производная 3x равна 3, поэтому в числителе стоит 3. А в знаменатель нам просто нужно положить квадратный корень из 3х в квадрате плюс 1:

f(x)=\text{arcsenh}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{\sqrt{(3x)^2+1}}=\cfrac{3}{\sqrt{9x^2+1}}

Пример 2

f(x)=\text{arcsenh}(x^3)

Чтобы получить гиперболический арксинус функции x в кубе, мы должны применить ту же формулу:

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

Производная x в кубе равна 3x 2 , поэтому производная гиперболического арксинуса x, возведенного в 3, будет равна:

f(x)=\text{arcsenh}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3x^2}{\sqrt{\left(x^3\right)^2+1}}=\cfrac{3x^2}{\sqrt{x^6+1}}

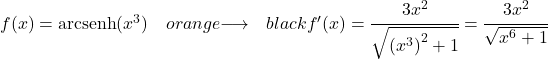
Доказательство гиперболической производной арксинуса

Продемонстрируем формулу производной гиперболического арксинуса:

y=\text{arcsenh}(x)

Сначала преобразуем гиперболический арксинус в гиперболический синус:

x=\text{senh}(y)

Из обеих частей равенства выводим:

1=\text{cosh}(y)\cdot y'

Мы очищаем вас:

y'=\cfrac{1}{\text{cosh}(y)}

Затем мы применяем тригонометрическое тождество, которое соединяет гиперболический синус и гиперболический косинус:

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{cosh}(y)=\sqrt{1+\text{senh}^2(y)}

y'=\cfrac{1}{\sqrt{1+\text{senh}^2(y)}}

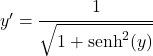
Но выше мы пришли к выводу, что x соответствует гиперболическому синусу y, поэтому уравнение остается:

y'=\cfrac{1}{\sqrt{1+x^2}}

Как видите, применив эти действия, мы получили формулу производной гиперболического арксинуса, чем и доказали.

Похожие товары

  • Формула производной гиперболического секанса
  • Формула производной арсеканса
  • Формула секущей производной
  • Формула производной арксинуса
  • формула синусоидальной производной

Оставьте комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Прокрутить вверх