Производная гиперболического арккосинуса

На этой странице вы увидите, чему равна производная гиперболического арккосинуса (формула). Вы также найдете упражнения, решаемые шаг за шагом для производных гиперболического аркосинуса функции. И, наконец, вас ждет демонстрация формулы производной этого типа тригонометрической функции.

Формула производной гиперболического аркосинуса

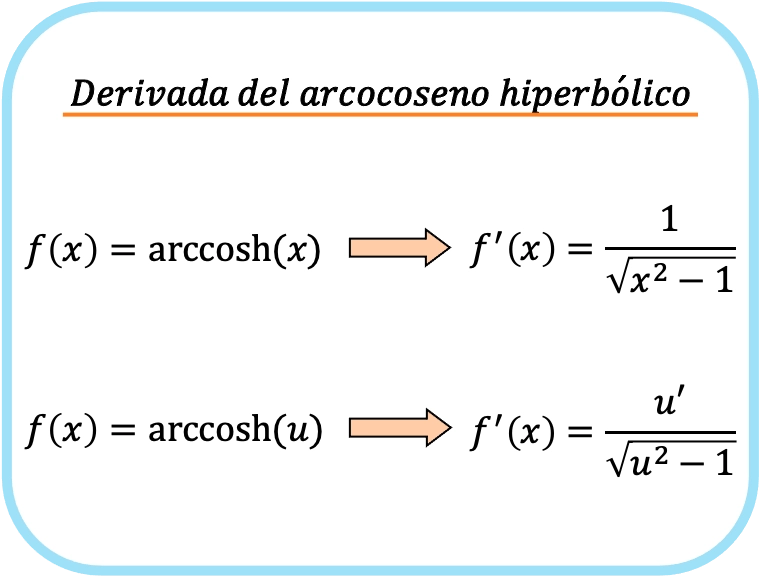
Производная гиперболического арккосинуса x равна единице по квадратному корню из x в квадрате минус 1.

f(x)=\text{arccosh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2-1}}

Следовательно, производная гиперболического аркокосинуса функции равна частному производной этой функции, деленному на квадратный корень этой функции, возведенный в квадрат минус один.

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

Вторая формула включает в себя правило цепочки и поэтому может использоваться для вывода любого гиперболического арккосинуса. Фактически, если мы заменим x на u, мы получим первую формулу. Вместо этого первая формула работает только для гиперболической производной арккосинуса x.

производная гиперболического арккосинуса

Гиперболический арккосинус является обратной функцией гиперболического косинуса, поэтому эти две функции связаны. Вы можете увидеть формулу производной этой тригонометрической функции, нажав здесь:

➤ См.: формула производной гиперболического косинуса

Примеры гиперболической производной арксинуса

Пример 1

f(x)=\text{arccosh}(5x)

Чтобы найти производную гиперболического арккосинуса, нам нужно использовать соответствующую формулу:

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

Следовательно, в числитель дроби нам нужно поставить производную от 5х, которая равна 5. А в знаменатель нам нужно просто положить корень квадратный из аргумента функции, возведенный в квадрат минус 1:

f(x)=\text{arccosh}(5x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{5}{\sqrt{(5x)^2-1}}=\cfrac{5}{\sqrt{25x^2-1}}

Пример 2

f(x)=\text{arccosh}(x^4-5x^2)

Функция, которую нужно вывести из этого упражнения, представляет собой гиперболический арккосинус, поэтому для ее получения мы используем следующую формулу:

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

Таким образом, в числителе запишем производную аргумента функции, а в знаменателе — квадратный корень из функции аргумента, возведенного в 2 минус 1:

f(x)=\text{arccosh}(x^4-5x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{4x^3-10x}{\sqrt{\left(x^4-5x^2\right)^2-1}}

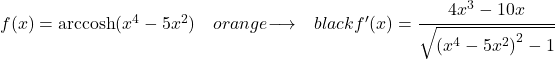
Доказательство производной гиперболического аркосинуса

Наконец, мы продемонстрируем формулу производной гиперболического аркосинуса.

y=\text{arccosh}(x)

Сначала преобразуем гиперболический арккосинус в гиперболический косинус:

x=\text{cosh}(y)

Выводим из обеих частей равенства:

1=\text{senh}(y)\cdot y'

Мы очищаем вас:

y'=\cfrac{1}{\text{senh}(y)}

Теперь мы используем тригонометрическое тождество, связывающее гиперболический синус и гиперболический косинус, чтобы изменить знаменатель:

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{senh}(y)=\sqrt{\text{cosh}^2(y)-1}

y'=\cfrac{1}{\sqrt{\text{cosh}^2(y)-1}}

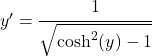
Однако сначала мы пришли к выводу, что x эквивалентен гиперболическому косинусу y, поэтому уравнение остается:

y'=\cfrac{1}{\sqrt{x^2-1}}

Похожие товары

  • Формула производной гиперболического косеканса
  • Формула производной арккосеканса
  • Формула производной косеканса
  • Формула производного арккозина
  • Формула производной косинуса

Оставьте комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Прокрутить вверх