Векторное вычитание

На этой странице вы увидите, как вычесть два вектора как графически, так и численно. Для их графического вычитания есть три метода: параллелограмм, треугольник и многоугольник. Здесь можно разграничить преимущества и недостатки каждого метода. Кроме того, вы найдете примеры, упражнения и задачи, решаемые шаг за шагом.

Как графически вычесть два вектора?

Существует несколько способов геометрического вычитания векторов. Очевидно, что со всеми ними получается один и тот же результат, но мы объясним вам все способы, чтобы вы могли выбрать тот, который вам больше по душе. 👌

Чтобы вычесть только 2 вектора, есть две графические процедуры: метод параллелограмма и метод треугольника . Однако, если мы хотим решить вычитание 3 или более векторов, нам нужно использовать метод многоугольника .

Итак, без лишних слов, ниже у вас есть объяснения всех этих методов.

Метод или правило параллелограмма

Правило параллелограмма или метод параллелограмма — это процедура, позволяющая очень простым способом найти вычитание двух векторов через их графическое представление. Для применения этого процесса необходимо выполнить следующие шаги:

1. Сначала мы представляем два вектора на графике и располагаем их в одной и той же точке приложения, то есть помещаем начала обоих векторов в одну и ту же точку.
2. Во-вторых, мы рисуем вектор, противоположный вектору, который вычитается в операции, или, другими словами, мы обращаем вектор, который вычитает.
3. Затем мы рисуем линию, параллельную вектору с измененным знаком, в конце добавляемого вектора. И повторяем процесс с другим вектором. Так что у нас получится рисунок параллелограмма (отсюда и название правила).
4. Наконец, результатом вычитания будет вектор, идущий от общего начала двух векторов до точки пересечения двух параллельных прямых.

Рассмотрим следующий общий пример, в котором два вектора вычитаются с использованием метода параллелограмма:

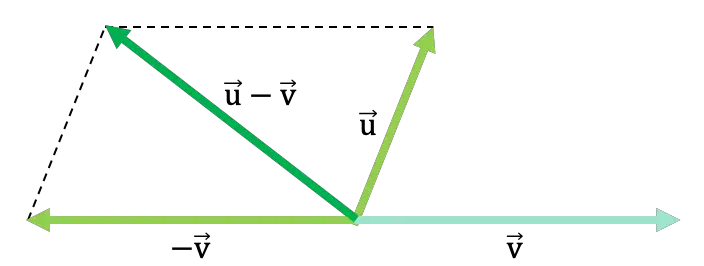
Метод или правило треугольника

Метод треугольника — это еще одна процедура, с помощью которой два вектора можно вычесть из их графика. В этом случае необходимо выполнить следующие действия:

1. Поместите два вектора в одну и ту же точку приложения, то есть так, чтобы оба вектора имели одну и ту же точку, что и их начало.
2. Результатом вычитания вектора является отрезок, идущий от конца вычитающего вектора до конца другого вектора. Если вы присмотритесь, то увидите, что треугольник состоит из двух вычтенных векторов и вычтенного вектора.

Вот пример вычитания вектора с использованием метода треугольника:

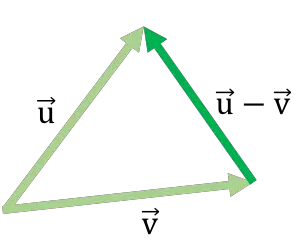
Этот способ вычитания векторов аналогичен методу «голова и хвост» , используемому для сложения векторов .

полигональный метод

После того, как мы увидели, как графически решить вычитание двух векторов, мы увидим, как это делается, когда у нас более двух векторов.

Если вы хотите вычесть три или более векторов, есть способ ускорить вычисления и вычесть все векторы одновременно. Этот метод называется методом полигонов и состоит в последовательном применении метода сложения векторов «голова к хвосту».

Теперь вы, наверное, думаете: добавить векторы? Неправильно поправили… Ну нет! да да

Оказывается, вычитание двух векторов — это то же самое, что сложение вектора плюс вектор, противоположный (или отрицательный) вектору вычитания. Это связано со свойствами сложения и вычитания векторов:

Таким образом, шаги, которые нам необходимо выполнить, чтобы вычесть 3 или более векторов с помощью метода многоугольника:

1. Во-первых, нам нужно найти обратный вектор каждого вектора вычитания. Это так же просто, как поменять направление и направление всех вычитаемых векторов.
2. Затем мы помещаем каждый противоположный вектор один за другим рядом с вектором, который вы не вычитаете. Так что начало вектора совпадает с концом другого вектора.
3. Наконец, результатом вычитания вектора является вектор, полученный путем соединения начала первого вектора с концом последнего вектора.

Посмотрите на следующий пример, где вычитание выполняется с 4 векторами:

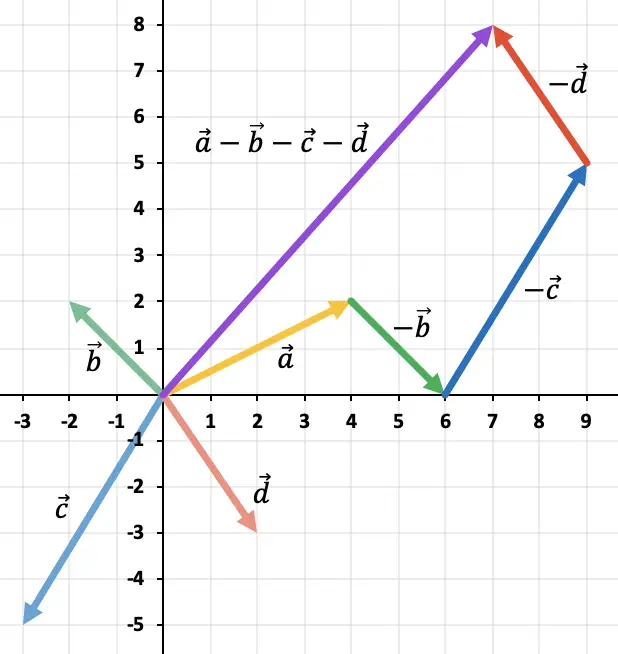
Обратите внимание: чтобы найти вектор, противоположный вектору, две компоненты указанного вектора должны изменить знак.

Как численно рассчитать вычитание двух векторов?

Как только мы уже знаем, как вычитать векторы из графика, мы увидим, как рассчитать вычитание векторов численно или алгебраически.

Например, вычитание между векторами

И

Восток:

Решенные задачи на вычитание векторов

Упражнение 1

Графический расчет векторного вычитания

меньше

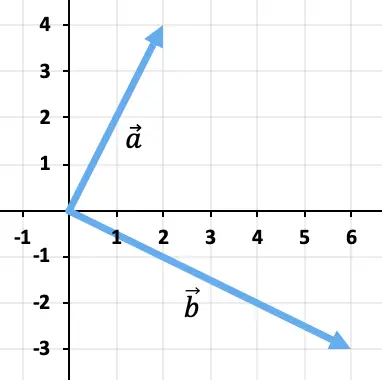
Чтобы вычесть два вектора, мы воспользуемся методом треугольника. Точки уже размещены в одной и той же точке приложения (начале координат), поэтому результатом вычитания будет вектор, идущий от конца

в конце

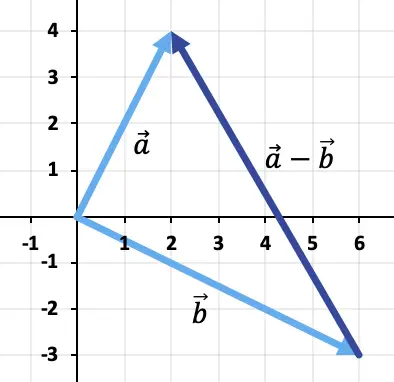
Упражнение 2

Найти вычитание векторов графически

меньше

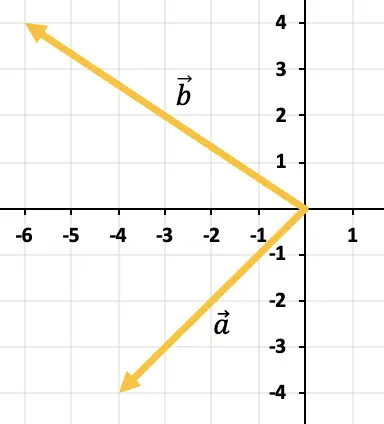
Чтобы вычесть два вектора, мы воспользуемся правилом треугольника. Точки уже размещены в одной и той же точке приложения (в начале оси X и оси Y), поэтому результатом вычитания будет вектор, идущий от конца

в конце

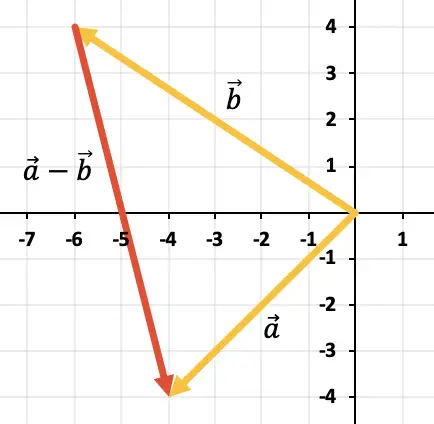
Упражнение 3

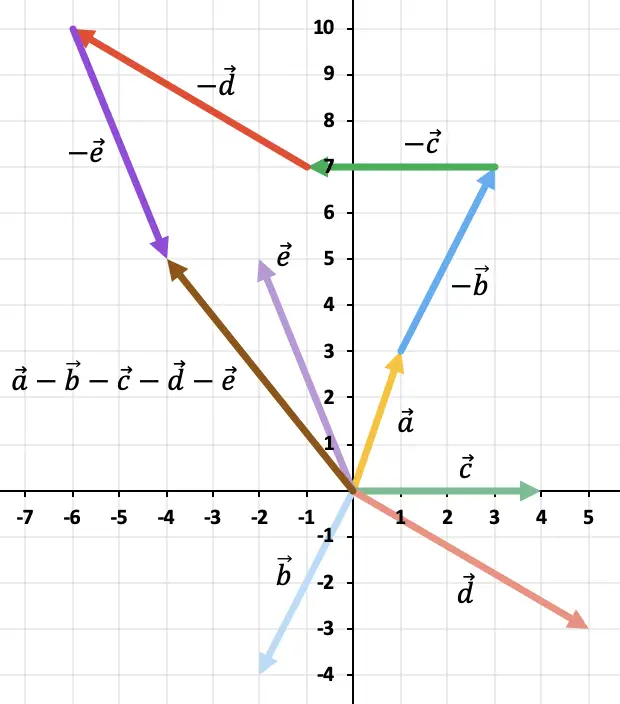
Графически решим следующую векторную операцию:

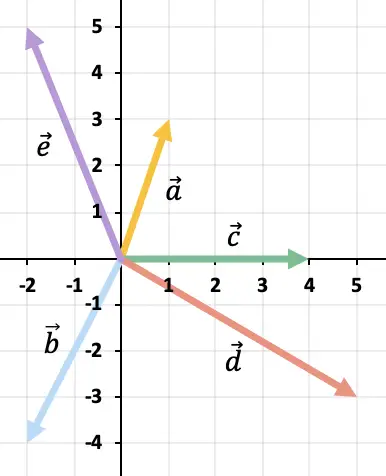
Поскольку векторов более двух, мы будем использовать правило многоугольника для решения вычитания векторов. Для этого нам нужно представить друг за другом противоположные векторы остальных векторов. И результатом будет вектор, который начинается с начала координат вектора.

туда, где заканчивается последний противоположный вектор.

Упражнение 4

Численно определите результат вычитания следующих векторов:

Чтобы численно вычесть два вектора, необходимо вычесть их соответствующие координаты:

Упражнение 5

Аналитически решите следующую векторную операцию:

Чтобы вычесть векторы численно (или аналитически), мы должны вычесть их соответствующие компоненты: