Вычислить точку пересечения или пересечения двух линий

Здесь вы узнаете, как рассчитывается точка разреза (или пересечение) между двумя линиями. Вы также увидите примеры и сможете попрактиковаться, выполняя упражнения шаг за шагом.

Что такое точка отсечения или пересечения двух линий?

Точка пересечения (или разреза) двух линий — это точка пересечения двух разных линий. Поэтому, когда две разные линии имеют точку пересечения или разреза, это означает, что они совпадают в одной точке.

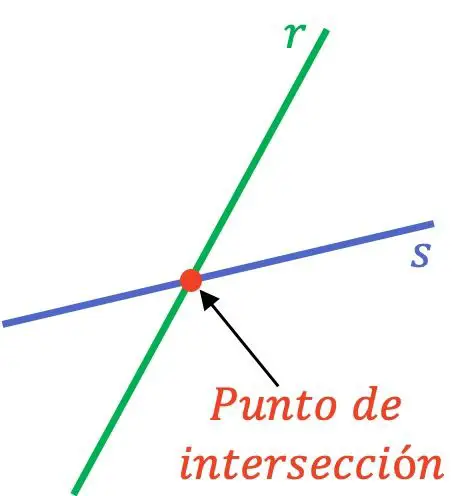
Чтобы две прямые пересеклись в одной точке, они должны быть пересекающимися прямыми, поскольку параллельные прямые не соприкасаются ни в одной точке.

Если вы сейчас точно не помните, что такое пересекающиеся линии, мы рекомендуем посетить нашу страницу «Примеры пересекающихся линий» , где вы найдете подробное объяснение того, что это за типы линий и как определить, пересекаются две линии или нет.

Как рассчитать точку отсечки или пересечения двух линий?

После того, как мы увидели определение точки пересечения или пересечения двух линий, давайте теперь посмотрим, как рассчитывается указанная точка.

Чтобы найти точку пересечения (или пересечения) двух линий, необходимо сначала убедиться, что эти две линии не параллельны, поскольку, если это две параллельные линии, они не будут пересекаться ни в одной точке. Поэтому сначала нужно знать, как определить , когда две прямые параллельны , а когда нет; Если вы не помните, как это делать, вы можете посмотреть его еще раз, перейдя по ссылке.

Как только мы узнаем, что две линии не параллельны, чтобы определить точку пересечения (или пересечения) между двумя линиями, мы должны решить систему уравнений, образованную уравнением каждой линии. И результатом указанной системы уравнений будут координаты точки пересечения (или пересечения) двух линий.

Пример того, как найти точку пересечения или пересечения двух линий

В качестве примера мы решим задачу, чтобы вы увидели, как найти точку пересечения (или пересечения) между 2-мя прямыми:

• Найдите точку пересечения следующих двух линий:

Во-первых, линии не параллельны, поскольку имеют разные наклоны, поэтому обе они пересекаются в точке на декартовой плоскости.

Чтобы это узнать, надо решить систему уравнений, составленную из уравнений каждой строки:

В данном конкретном случае будем решать систему методом уравнения, так как две неизвестные

уже решены (обе строки имеют явный вид уравнения):

Удаляем значение переменной

И как только ты узнаешь, сколько это стоит

Подставим его значение в любое уравнение, чтобы найти значение

Итак, координаты точки пересечения двух линий:

Решенные проблемы точки пересечения или пересечения двух линий

Упражнение 1

Какова точка пересечения или пересечения следующих двух линий?

Во-первых, линии не параллельны, поскольку имеют разный наклон, поэтому в какой-то точке плоскости они встретятся.

Для расчета указанной точки необходимо решить систему уравнений, образованную уравнением каждой линии:

В этом случае будем решать систему уравнений методом уравнения, так как две неизвестные

уже решены (обе строки имеют явный вид уравнения):

Удаляем значение переменной

И как только ты узнаешь, сколько это стоит

Подставим его значение в любое уравнение, чтобы найти значение

Таким образом, координаты точки пересечения двух линий:

Упражнение 2

Найдите точку пересечения или пересечения следующих двух линий:

право

Оно выражается в виде неявного (или общего) уравнения, поэтому сначала передадим его в виде явного уравнения, чтобы узнать значение его наклона:

Таким образом, две линии имеют разные наклоны и, следовательно, между ними есть точка пересечения.

Для расчета указанной точки необходимо решить систему уравнений, образованную уравнением каждой линии:

Решаем систему уравнений методом уравнения:

Удаляем значение переменной

И как только ты узнаешь, сколько это стоит

Мы подставляем его значение в любое уравнение, чтобы найти значение

Таким образом, координаты точки пересечения двух линий:

Упражнение 3

Определите точку пересечения или пересечение следующих двух линий:

Прежде всего нам нужно знать, две ли это параллельные прямые или нет. Для этого мы проверим, пропорциональны ли векторы направления двух линий.

право

определяется в виде параметрических уравнений, поэтому компонентами его вектора направления являются коэффициенты перед параметром

И, с другой стороны, линия

описывается в виде неявного уравнения, поэтому его вектор направления равен:

Так как компоненты двух векторов направления не пропорциональны друг другу, следовательно, две линии не параллельны.

А поскольку две линии не параллельны, это означает, что между ними действительно есть точка пересечения. Для его расчета необходимо решить систему уравнений, образованную уравнением каждой линии:

В этом случае, как и строка

имеет форму параметрических уравнений, необходимо подставить выражение каждого параметрического уравнения в уравнение другой строки:

Теперь решим полученное уравнение:

и замените значение

найденные в параметрических уравнениях для нахождения координат точки разреза:

Итак, точка пересечения двух линий: