Вычислить наименьшее общее кратное (lcm)

Наименьшее общее кратное (НОК) двух или более чисел — это наименьшее (ненулевое) кратное, общее для этих чисел. Это операция, обратная наибольшему общему делителю , хотя вычисляется аналогичными методами. Если вы хотите узнать, как рассчитать НОК, рекомендуем продолжить чтение, поскольку в этой статье мы объясним все процедуры (от самых простых до самых сложных) по нахождению наименьшего общего кратного набора чисел.

калькулятор lcm

Прежде чем мы начнем говорить о том, как получить lcm, мы хотим, чтобы вы знали, что на этой странице у нас есть калькулятор наименьших общих кратных . С его помощью вы сможете вычислить 1см всех нужных чисел и сравнить результаты своих упражнений, чтобы увидеть, правильно ли вы их решили.

Чтобы использовать менее распространенный калькулятор кратных, введите целые числа, разделенные запятой:

рассчитать lcm

Как вычислить наименьшее общее кратное?

Чтобы найти наименьшее общее кратное двух или более чисел, вам нужно воспользоваться одним из трех методов, которые мы объясним ниже. Далее, когда мы подробно расскажем о каждой из процедур, которые вы можете выбрать, мы также расскажем вам, каковы их преимущества и недостатки. Таким образом, вы будете знать, какой из них выбрать в каждой ситуации, чтобы легко и быстро решить рассматриваемую LCM.

Метод 1: множественный список

Первый метод — создать список кратных чисел, которые вы хотите вычислить в LCM. Затем вам нужно найти наименьшее значение, которое повторяется во всех списках , таким образом у вас будет наименьшее общее кратное. Дальше мы увидим это на примере: lcm(5, 6).

Способ 2: факториальное разложение

Во-вторых, мы можем факторизовать числа. Более конкретно, этот метод облегчит вычисление PCM больших чисел . Поскольку выполнение метода 1 при выполнении lcm больших чисел может быть медленным и утомительным просто потому, что нам придется писать очень длинные списки кратных. Поначалу эта вторая процедура может быть немного сложнее для понимания, но когда вы поймете механику, она имеет много преимуществ по сравнению с предыдущей. Тем не менее, давайте посмотрим, как следует поступить:

• Факториальное разложение: первым шагом будет разложение всех чисел, которые мы собираемся включить в LCM, на простые множители. Если вы не знаете , как разложить число на факториал , рекомендуем перейти по этой последней ссылке, там вы найдете первоклассное объяснение, как быстро и эффективно упростить числа.
• Создайте одно математическое выражение: когда у нас есть все числа, выраженные в виде простых делителей, мы выберем общие и необычные числа, возведенные в наибольшую степень. Затем вы записываете их как одно математическое выражение и, наконец, решаете необходимые умножения и/или степени. И у вас уже будет числовое значение lcm.

Способ 3: Математическая формула

Существует последний способ получить наименьшее общее кратное, который состоит из использования НОД и следующей математической формулы:

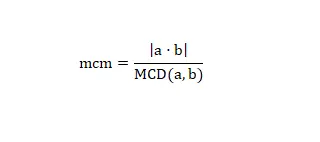
Используя эту формулу, мы можем вычислить 1см любого числа. Давайте посмотрим на реальный пример: если мы хотим вычислить lcm (2.6), нам просто нужно решить операцию (2 x 6)/2 = 6. И мы уже решим вычисление, как видите, это простой метод. и быстро , если у вас есть НОД или вы можете легко его вычислить.

Советы по быстрому расчету lcm

Когда вы освоите три метода, которые мы только что объяснили, мы рекомендуем вам прочитать свойства наименьшего общего кратного , о которых мы сейчас поговорим. Поскольку благодаря им вы сможете определить некоторые конкретные ситуации, в которых LCM можно рассчитать очень быстро, без необходимости использовать уже объясненные стратегии.

• Первое число, делящееся на второе: если мы хотим вычислить наименьшее общее кратное a и b, когда a делит b, то ppcm этих двух чисел будет наибольшим (в данном случае b). Например, если вы хотите вычислить 1см 2 и 8, результат будет наибольшим, следовательно, 8.
• Два простых числа. В случае нахождения двух простых чисел самый быстрый способ — умножить их вместе, и результатом будет число ppcm. Это логично, так как его наибольший общий делитель равен 1, а значит, мы не сможем разложить число на более простые множители, чем само число, и, следовательно, сможем только перемножить их вместе. Например, НОК чисел 3 и 5 будет результатом их произведения: 3 х 5 = 15.

Как получить наименьшее общее кратное дробей?

Когда мы хотим решить задачу сложения или вычитания дробей, нам нужно вычислить наименьший общий знаменатель, который аналогичен lcm, но применяется к дробям. По сути, мы ищем 1 см двух знаменателей, чтобы затем выразить сумму в виде одной дроби. Если вы хотите увидеть, как наименьший общий знаменатель применяется к вычислению реальной дроби, вы можете перейти по этой ссылке .

Lcm на научном калькуляторе

Ключ LCM, который есть на любом научном калькуляторе, позволяет вычислить наименьшее общее кратное двух целых чисел. В случае калькуляторов Casio синтаксис или процедура, которой вам необходимо следовать, выглядит следующим образом. Сначала вы нажимаете APHA + MCM (последняя клавиша будет помечена коричневым цветом). Как только это будет сделано, вы можете ввести оба числа, но помните, что вы должны разделить их запятой ( SHIFT + , ). Наконец, вы получите наименьшее общее кратное, нажав кнопку равенства.

Упражнения LCM решаются шаг за шагом

Далее мы шаг за шагом покажем вам три примера решения наименьшего общего кратного . Таким образом, вы можете попытаться решить эти проблемы и немного попрактиковаться в том, что мы объяснили в этой статье. Если вы хотите усвоить концепции, важно попытаться решить упражнения, поскольку необходимо применить теорию к реальности. Тем не менее, мы позволяем вам практиковаться с упражнениями:

Вычислите lcm чисел 4 и 6.

Вычислите lcm чисел 6 и 9.

Вычислите lcm 30 и 40.