Верхняя и нижняя треугольная матрица

На этой странице вы увидите, что такое треугольная матрица и различные типы треугольных матриц, а также примеры. Кроме того, вы узнаете, как вычислить определитель треугольной матрицы и каковы свойства этой очень интересной матрицы. Наконец, мы также объясним, что такое матрица Хессенберга, поскольку это матрица, связанная с треугольными матрицами.

Что такое треугольная матрица?

Определение треугольной матрицы:

Треугольная матрица — это квадратная матрица, в которой все элементы выше или ниже главной диагонали равны нулю (0).

Треугольные матрицы широко используются в вычислениях линейной алгебры, поскольку инвертировать треугольную матрицу, вычислять ее определитель или даже решать системы линейных уравнений с помощью этого типа матриц гораздо проще, чем с матрицами, имеющими элементы, отличные от 0 во всех позициях. .

верхняя треугольная матрица

Верхнетреугольная матрица – это квадратная матрица, элементы которой ниже главной диагонали равны нулю (0).

Пример верхней треугольной матрицы:

нижняя треугольная матрица

Нижнетреугольная матрица — это квадратная матрица, имеющая ноль (0) в каждом элементе, находящемся выше главной диагонали.

Пример нижней треугольной матрицы:

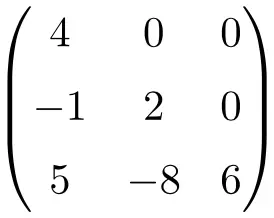
Иногда эти матрицы также называют буквой U для верхней треугольной матрицы и буквой L для нижней треугольной матрицы. Хотя эта номенклатура в основном используется в английском языке, на самом деле буква U означает верхнюю треугольную матрицу , а буква L — нижнюю треугольную матрицу .

Примеры треугольных матриц

Треугольная матрица размерности 2 × 2

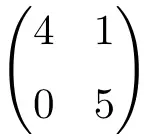
Треугольная матрица порядка 3×3

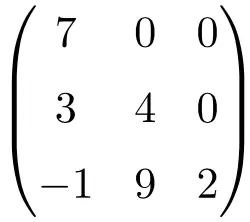
треугольная матрица размером 4х4

Определитель треугольной матрицы

Определитель треугольной матрицы , будь то верхняя или нижняя треугольная, является произведением элементов на главной диагонали.

Взгляните на следующее упражнение, решенное, как достаточно вычислить умножение элементов главной диагонали треугольной матрицы, чтобы найти ее определитель:

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

Эту теорему легко продемонстрировать: просто вычислите определитель треугольной матрицы по блокам (или кофакторам). Эта демонстрация подробно описана ниже с использованием общей треугольной матрицы:

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

С другой стороны, мы знаем, что матрица обратима, если ее определитель отличен от 0. Итак, если ни один элемент на главной диагонали не равен 0, треугольная матрица также будет обратимой и, следовательно, будет правильной матрица.

Свойства треугольной матрицы

Теперь посмотрим, каковы свойства треугольных матриц:

Произведение двух верхних треугольных матриц равно одной верхней треугольной матрице. И наоборот: умножение двух нижних треугольных матриц дает еще одну нижнюю треугольную матрицу.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

Транспонирование верхней треугольной матрицы является нижней треугольной матрицей, и наоборот: транспонирование нижней треугольной матрицы является верхней треугольной матрицей.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

Треугольная матрица обратима, если все ее элементы на главной диагонали ненулевые, то есть отличны от нуля. В таком случае обратная верхней (нижней) треугольной матрице также является верхней (нижней) треугольной матрицей.

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

Кроме того, главная диагональ инвертированной матрицы всегда будет содержать обратные элементы главной диагонали исходной треугольной матрицы.

Любая диагональная матрица является одновременно верхней треугольной матрицей и нижней треугольной матрицей, например:

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

Таким образом, скалярная матрица — это также верхняя и нижняя треугольная матрица. Например, единичная матрица:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Очевидно, что нулевая матрица также является верхней и нижней треугольной матрицей, поскольку элементы выше и ниже главной диагонали равны 0:

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Собственные значения (или собственные значения) треугольной матрицы — это элементы главной диагонали.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

Верхняя или нижняя треугольная матрица всегда способна к диагонализации на основе собственных векторов (или собственных векторов).

Любую матрицу можно разложить на произведение нижней треугольной матрицы и верхней треугольной матрицы . То есть любую матрицу можно преобразовать в умножение треугольной матрицы. При этом, если матрица обратима, это преобразование уникально. Для факторизации матрицы часто используется метод LU-разложения.

Триангуляризировать матрицу

Существует несколько теорем о матрицах, которые можно треугольизировать, меняя основание. Однако здесь мы увидим, как триангулировать матрицу, применяя к линиям элементарные преобразования , как в методе Гаусса.

Например:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

И таким образом мы уже триангуляризировали исходную матрицу.

Напомним, что элементарные преобразования, разрешенные между строками в методе Гаусса:

Замените строку линейной комбинацией других линий.
Умножьте или разделите все члены подряд на число, отличное от 0.
Редактировать строки заказа.

Матрица Хессенберга

Определение матрицы Хессенберга следующее:

Матрица Хессенберга представляет собой «почти» треугольную матрицу, то есть все ее элементы равны нулю, начиная с первой субдиагонали (верхняя матрица Хессенберга) или первой супердиагонали (нижняя матрица Хессенберга).

Я уверен, что это лучше всего понять на примере верхней матрицы Хессенберга и еще одного примера нижней матрицы Хессенберга:

Верхняя матрица Хессенберга

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

Нижняя матрица Хессенберга

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

Матрица, которая является одновременно верхней и нижней матрицей Хессенберга, является трехдиагональной матрицей .

Эта матрица названа в честь Карла Хессенберга, выдающегося немецкого инженера и математика XX века.

Наконец, этот тип матрицы имеет особенность: если ее умножить на треугольную матрицу, результатом всегда будет матрица Хессенберга.