▷ Вычислить векторное произведение двух векторов (примеры)

На этой странице объясняется, что такое векторное произведение двух векторов и как оно рассчитывается. Вы также увидите, как найти направление и направление векторного произведения, используя правило правой руки (или штопор). Более того, вы найдете способы использования этого типа операций, а также примеры, упражнения и задачи, решаемые шаг за шагом.

Чему равно векторное произведение двух векторов?

В математике векторное произведение — это операция между двумя векторами в трехмерном пространстве (в R3). Результатом этой векторной операции является вектор с направлением, перпендикулярным двум перемноженным векторам, и с модулем, равным произведению модулей векторов-множителей на синус образуемого ими угла. Другими словами, его формула такова:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)$

Как вы видите в предыдущей формуле, векторное произведение обозначается

$\bm{\times}$

, поэтому его еще называют перекрестным произведением. Его также иногда называют векторным произведением Гиббса, поскольку он его изобрел.

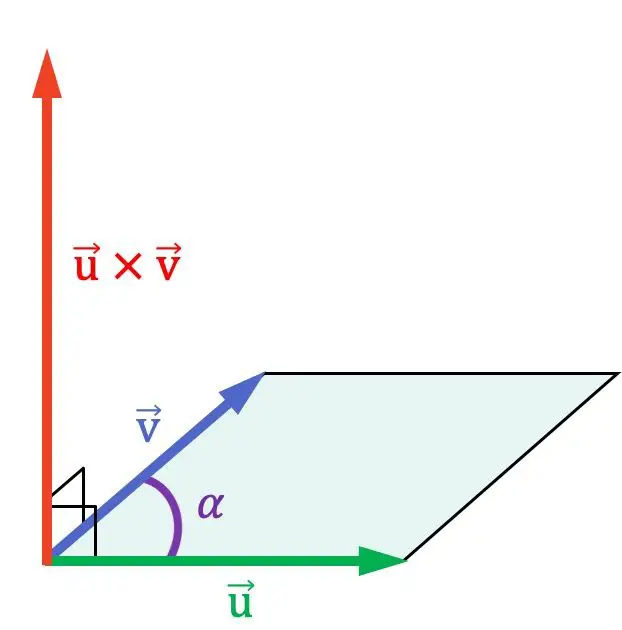
Как вы можете видеть в предыдущем графическом представлении, векторное произведение перпендикулярно двум векторам, на которые они перемножаются, и, следовательно, оно нормально к плоскости, которая их содержит.

Формула расчета векторного произведения двух векторов

Если мы знаем декартовы координаты векторов, самый простой способ вычислить их векторное произведение — найти определитель 3×3. Посмотрите, как это делается:

Рассмотрим любые два вектора:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Его векторное произведение:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}$

Где векторы

$\vv{i}, \vv{j},\vv{k}$

Это единичные векторы в направлениях осей X, Y и Z соответственно.

Давайте посмотрим пример того, как вычислить векторное произведение двух векторов:

$\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)$

Чтобы определить векторное произведение векторов, необходимо составить следующий определитель третьего порядка:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}$

В этом случае определитель будем решать с помощью адъювантов или кофакторов (можно также использовать правило Саррюса):

$\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}$

Таким образом, результатом векторного произведения двух векторов будет:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}$

Определяет направление и направление векторного произведения

Иногда нам не нужно знать компоненты вектора, полученного в результате векторного произведения, но достаточно найти его модуль, его направление и направление. Такое часто случается в физике, особенно при расчете сил.

Таким образом, существует несколько правил нахождения направления и направления векторного произведения, наиболее известными из которых являются правило правой руки , либо тремя пальцами, либо всей рукой, и правило штопора (или винта) . Вы можете использовать любое из них, поэтому вам не обязательно знать их все, мы все равно объясним вам три правила, чтобы вы могли придерживаться того, которое вам больше нравится. 😉

Правило правой руки (3 пальца)

Версия правила или закона правой руки с тремя пальцами предполагает выполнение следующих шагов:

Поместите указательный палец правой руки к первому вектору векторного произведения.
$(\vv{\text{u}}).$
Поместите средний палец (или средний палец) правой руки ко второму вектору векторного произведения.
$(\vv{\text{v}}).$
Полученное положение большого пальца указывает направление и направление векторного произведения.
$(\vv{\text{u}}\times\vv{\text{v}}).$

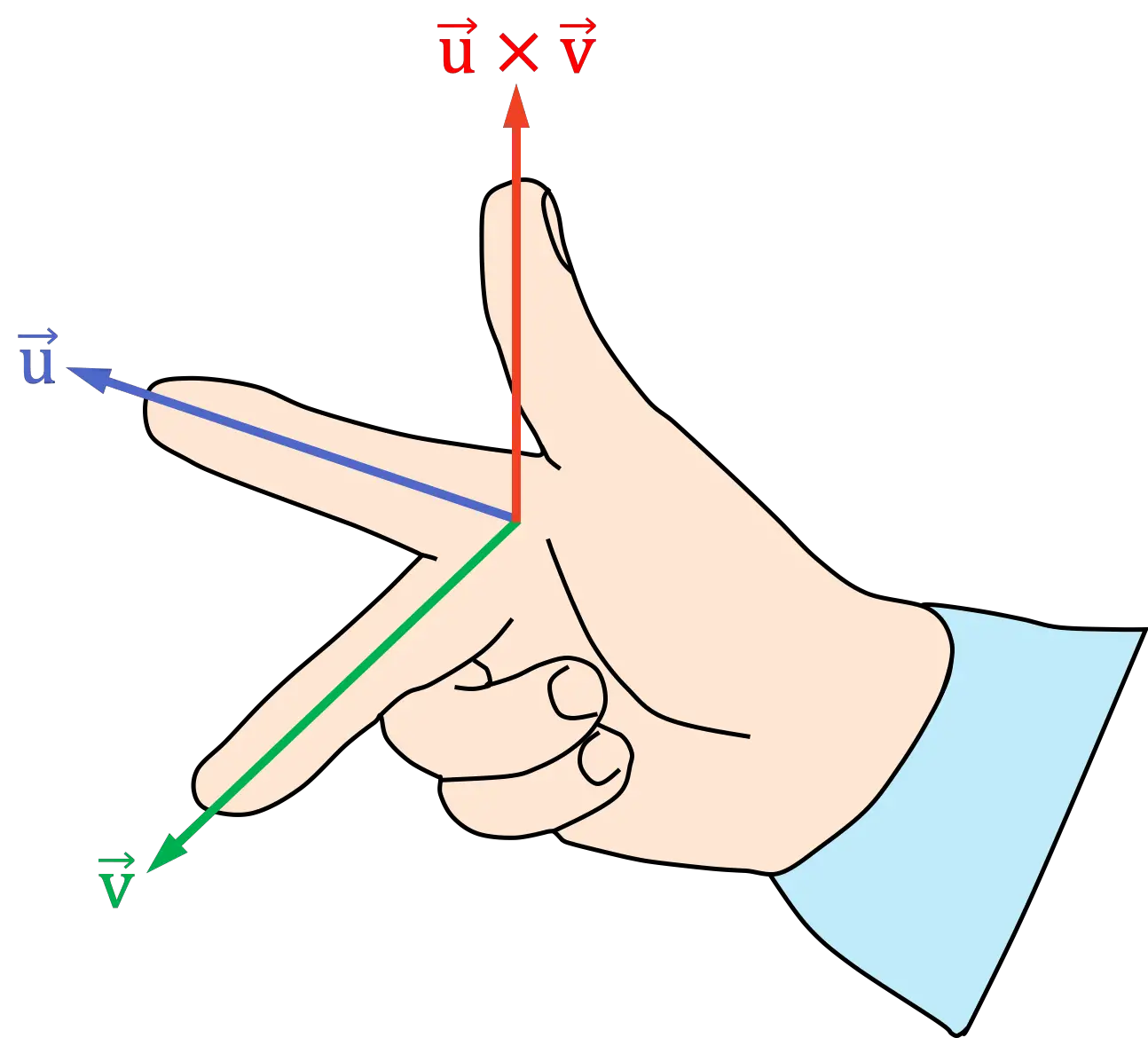
Правило правой руки (ладонь)

Ладонная версия правила или закона правой руки очень похожа на предыдущее правило. Чтобы применить его, необходимо выполнить следующие шаги:

Поместите правую руку пальцами в том же направлении, что и первый вектор векторного произведения.
$(\vv{\text{u}}).$
Закройте правую руку, переместив пальцы ко второму вектору векторного произведения.
$(\vv{\text{v}}).$

Сомкнуть руку нужно с той стороны, где угол (или расстояние) между векторами меньше.
Полученное положение большого пальца определяет направление векторного произведения.
$(\vv{\text{u}}\times\vv{\text{v}}).$

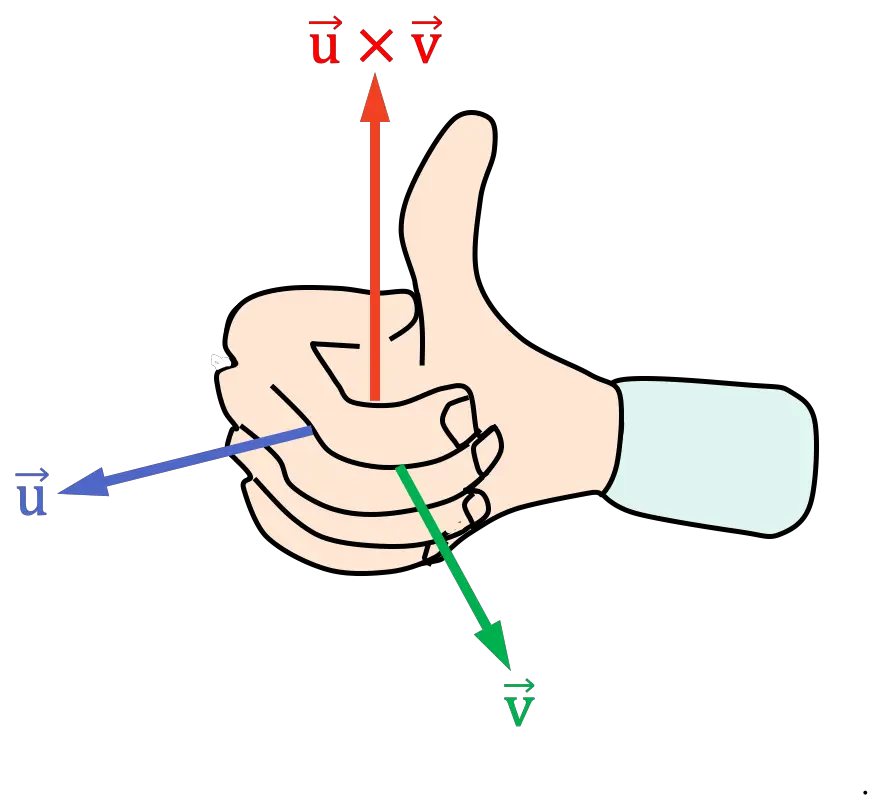
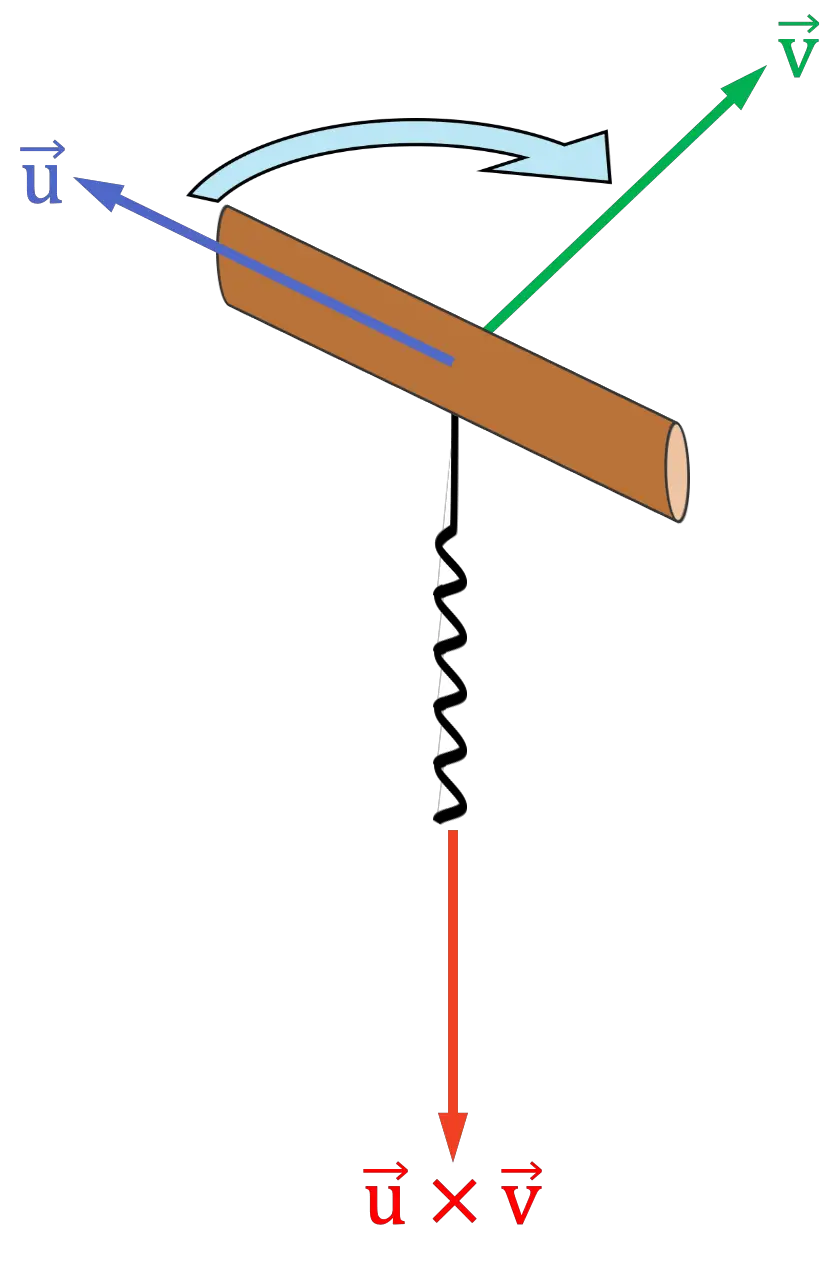
правило штопора

Правило штопора или винта аналогично правилу правой руки, в котором используется вся ладонь. Процедура следующая:

Используя свое воображение, поместите штопор (или винт) так, чтобы его ручка была направлена в том же направлении, что и первый вектор векторного произведения.
$(\vv{\text{u}}).$
Затем поверните штопор ко второму вектору векторного произведения.
$(\vv{\text{v}})$

как будто собираешься заткнуть его пробкой. Вам нужно повернуть штопор в ту сторону, где расстояние между векторами наименьшее.
Направление, в котором указывает спираль штопора, будет направлением и направлением векторного произведения.
$(\vv{\text{u}}\times\vv{\text{v}}).$

Свойства векторного произведения двух векторов

Перекрестное произведение двух векторов имеет следующие характеристики:

Антикоммутативное свойство: порядок векторов, входящих в векторное произведение, не безразличен, поскольку в зависимости от него меняется знак.

$\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}$

Распределительное свойство сложения и вычитания векторов:

$\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}$

$\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}$

Свойство однородности : умножение вектора векторного произведения на скаляр (действительное число) эквивалентно умножению результата векторного произведения на указанный скаляр.

$k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})$

Вектор, полученный в результате векторного произведения, перпендикулярен двум векторам, участвующим в операции.

$\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}$

Кроме того, если два вектора ортогональны, выполняются следующие уравнения:

$\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}$

Перекрестное произведение двух параллельных векторов равно нулевому вектору (или нулю).

$\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0$

Если мы не знаем угол, образованный двумя векторами, модуль их векторного произведения также можно вычислить по следующему выражению:

$\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}$

Вычислить площадь параллелограмма или треугольника, используя векторное произведение

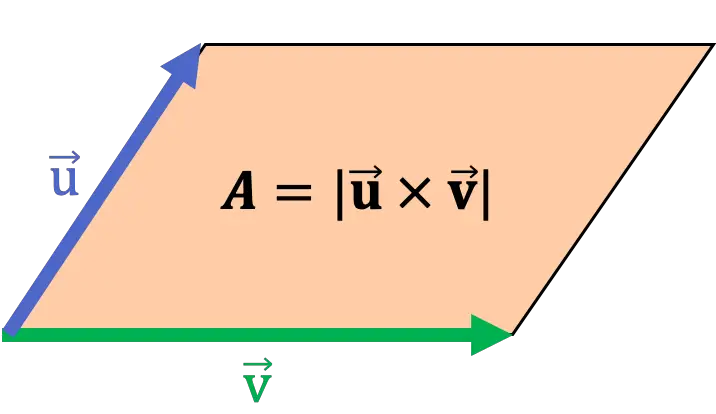
Геометрически модуль векторного произведения двух векторов совпадает с площадью параллелограмма, у которого эти два вектора являются сторонами. Следовательно, векторное произведение можно использовать для вычисления площади параллелограмма.

векторное произведение двух векторов в пространстве

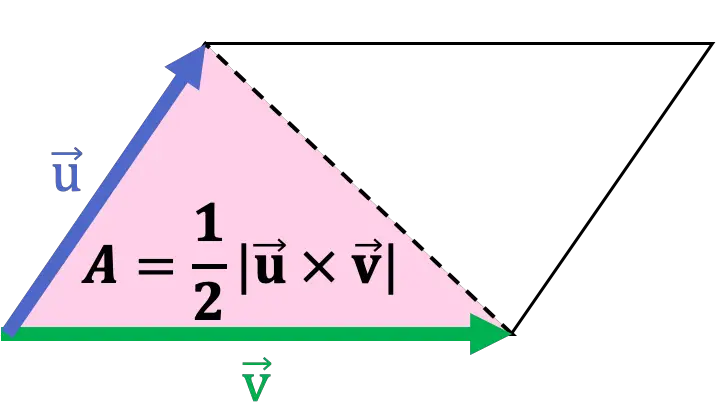
Кроме того, диагональ параллелограмма делит его на два треугольника, или, другими словами, треугольник — это половина параллелограмма. Таким образом, площадь треугольника равна половине модуля векторного произведения, принявшего две его стороны как векторы.

векторное произведение двух векторов в r2

Напомним, что модуль вектора в трехмерном пространстве является корнем суммы квадратов его координат:

$\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Это два применения векторного произведения двух векторов в области математики. Однако у него есть и другие применения, например, в физике он используется для расчета магнитного поля.

Решенные упражнения на векторные произведения векторов

Упражнение 1

Вычислите векторное произведение между следующими двумя векторами:

$\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)$

Посмотреть решение

Чтобы определить векторное произведение между векторами, мы должны решить следующий определитель размерности 3×3:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}$

В этом случае определитель будем решать с помощью адъювантов или кофакторов (но можно использовать и правило Сарруса):

$\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}$

Таким образом, результатом векторного произведения двух векторов будет:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}$

Упражнение 2

Найдите векторное произведение следующих двух векторов:

$\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)$

Посмотреть решение

Чтобы найти векторное произведение двух векторов, мы должны решить следующий определитель 3 × 3:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}$

В этом случае мы будем искать определитель с помощью сопряженных или кофакторов (хотя правило Сарруса можно использовать взаимозаменяемо):

$\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}$

Таким образом, результатом векторного произведения двух векторов будет:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}$

Упражнение 3

Зная модули двух векторов и угол, который они образуют:

$|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º$

Определите величину векторного произведения двух векторов.

Посмотреть решение

Мы можем легко вычислить модуль векторного произведения между двумя векторами, применив формулу:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}$

Упражнение 4

Из следующих векторов, содержащихся в плоскости экрана:

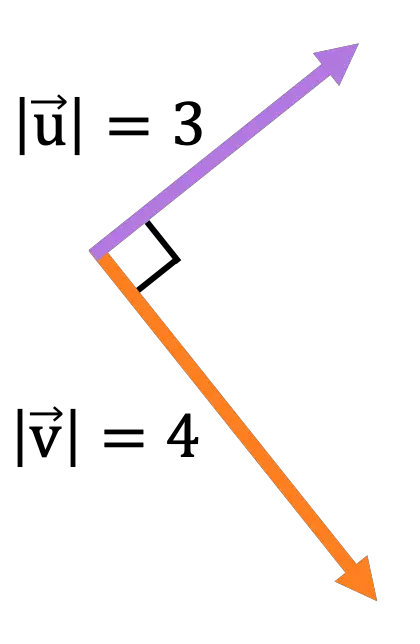
векторное произведение двух векторов в строке

Вычислите величину, направление и смысл вектора, полученного в результате следующей векторной операции:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert$

Посмотреть решение

Два вектора перпендикулярны, поэтому норма векторного произведения будет:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}$

С другой стороны, вектор, полученный в результате векторного произведения, перпендикулярен двум векторам, участвующим в операции, поэтому его направление будет перпендикулярно экрану.

И, наконец, используя правило прямой линии (или штопора), мы можем сделать вывод, что направление результирующего вектора будет внутрь экрана.

Упражнение 5

Вычислите площадь параллелограмма, две стороны которого имеют следующие векторы:

$\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)$

Посмотреть решение

Площадь параллелограмма совпадает с модулем векторного произведения векторов, его образующих. Поэтому мы вычисляем векторное произведение векторов:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}$

И затем ваш модуль:

$A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}$

Упражнение 6

Найдите площадь треугольника, вершинами которого являются следующие точки:

$A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)$

Посмотреть решение

Прежде всего, мы должны вычислить векторы, образующие стороны треугольника:

$\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)$

$\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)$

Площадь треугольника равна половине величины векторного произведения векторов, его образующих. Поэтому мы вычисляем векторное произведение векторов:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}$

После вашего модуля:

$\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19$

И наконец, площадь треугольника будет равна половине модуля:

$A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}$

Перекрестное произведение двух векторов (или перекрестное произведение)

Чему равно векторное произведение двух векторов?

Формула расчета векторного произведения двух векторов

Определяет направление и направление векторного произведения

Правило правой руки (3 пальца)

Правило правой руки (ладонь)

правило штопора

Свойства векторного произведения двух векторов

Вычислить площадь параллелограмма или треугольника, используя векторное произведение

Решенные упражнения на векторные произведения векторов

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Упражнение 6

Оставьте комментарий Отменить ответ