Бином Ньютона — это математическая формула, используемая для выражения суммы двух членов, возведенных в заданную степень . Эта формула, названная в честь британского математика Исаака Ньютона, используется во многих областях математики.
Например, он полезен в статистике, теории вероятностей, дифференциальном и интегральном исчислении. Теорема о биноме позволяет нам простым способом вычислить степень бинома.
Проще говоря, бином Ньютона основан на формуле, с помощью которой можно решить любое алгебраическое выражение вида (a+b) n . Несмотря на то, что эта формула названа в честь Исаака Ньютона, стоит отметить, что по поводу ее происхождения ведутся споры.
То есть некоторые исследования предлагают найти применение биномиальной теореме на Ближнем Востоке.
Когда был разработан бином Ньютона?
Биномиальная теорема Ньютона, также известная как бином Ньютона, была разработана в 1665 году и впервые сообщена в двух письмах от офицера Королевского общества в 1676 году .
Эти письма были ответом немецкому математику Готфриду Вильгельму фон Лейбницу, который стремился лучше понять математические исследования бесконечных рядов. Ньютон поделился результатами своей теоремы, а Лейбниц признал, что это полезный метод для получения результатов в квадратурах или рядах.
Это наблюдение позволило Ньютону прийти к выводу, что с бесконечными рядами можно действовать так же, как и с конечными полиномиальными выражениями . Хотя Ньютон никогда не публиковал свою теорему, британский математик Джон Уоллис опубликовал ее в своей «Алгебре» в 1685 году и приписал ее создание Ньютону.
Почему его называют биномом Ньютона?
Бином Ньютона назван в честь английского математика и физика Исаака Ньютона, разработавшего его в 17 веке . Ньютон не был первым, кто открыл эту теорему, но он был первым, кто доказал ее справедливость для любого натурального числа n.
Бином Ньютона — очень полезный математический инструмент в алгебре и исчислении, он широко используется в таких областях, как физика, статистика, инженерное дело и информатика.
Что такое биномиальная формула Ньютона?
Как мы упоминали ранее, бином Ньютона — это формула, по которой можно найти степени бинома . Чтобы найти указанную биномиальную степень, используются «биномиальные коэффициенты». Предыдущий термин относится к последовательностям комбинаций.
Имея это в виду, мы можем разбить биномиальные формулы Ньютона следующим образом:
- (а + b) 2 = а 2 + 2ab + b 2
- (а – б) 2 = а 2 – 2аб + б 2
- (а + б) 3 = а 3 + 3а 2 б + 3 аб 2 + б 3
Математические выражения, относящиеся к развитию (a+b) n , называются заметными объектами и позволяют получить общую формулу, которая представляет эту операцию для любого натурального числа «n».
Исследуя коэффициенты каждого результирующего многочлена, мы можем заметить последовательность, которая следует так называемому треугольнику Паскаля .
Последовательность треугольника Паскаля начинается с цифры 1, и в каждой последующей строке конечные цифры всегда равны 1. Промежуточные значения получаются сложением двух чисел из предыдущей строки, находящихся непосредственно над вычисляемым значением.
Как найти член в биноме Ньютона?
Для нахождения конкретного члена в биноме Ньютона используется общая формула:
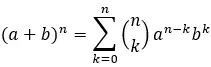
Золото:
a и b — коэффициенты бинома.
n — показатель степени бинома.
k — конкретный термин, который мы хотим найти.
Σ представляет собой сумму от k=0 до n.
[nk] — биномиальный коэффициент, рассчитываемый по следующей формуле:
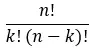
Следовательно, полностью развернутая формула такова:
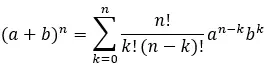
Пример решения бинома Ньютона
Как только эти значения найдены, они подставляются в формулу и выражение решается для получения конкретного члена. Например, если бы мы хотели найти пятый член бинома (2x + 3) 6 , мы бы имели:
один = 2x
б = 3
п=6
к = 5
Итак, используя формулу:
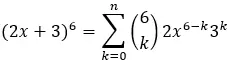
Пятый член соответствует k=5, поэтому мы имеем:
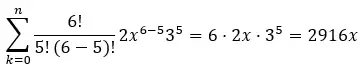
Следовательно, пятый член бинома (2x+3) 6 равен 2916x.
Что такое бином Ньютона пятой степени?
Бином Ньютона степени 5 — это алгебраическое выражение вида (a + b) 5 , где «a» и «b» — переменные, а показатель степени 5 указывает степень бинома . Разлагая это выражение, получаем квадратичный многочлен, состоящий из шести членов:
(a + b) 5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
Каждый член этого многочлена получается путем объединения коэффициентов бинома со степенями «a» и «b». Например, второй член (5a 4 b) получается путем умножения биномиального коэффициента (5 выберите 1 = 5) на «a», возведенную в четвертую степень, и на b, возведенную в первую степень.
Биномы Ньютона 5-й степени полезны в различных разделах математики и физики, таких как статистика, теория вероятностей и квантовая механика.
Каковы применения бинома Ньютона?
Бином Ньютона имеет множество применений в различных областях, в том числе:
- Вычисление вероятностей . Биномиальная теорема используется для расчета вероятностей биномиальных событий, таких как подбрасывание монеты или успех или неудача серии тестов.
- Теория чисел . Бином Ньютона используется для разложения многочленов и упрощения уравнений в теории чисел.
- Статистика : Бином Ньютона используется для расчета биномиальных распределений и при построении доверительных интервалов.
- Физика . В физике биномиальная теорема используется, среди других областей, в теории относительности и квантовой механике.
- Экономика и финансы : бином Ньютона используется для расчета текущей и будущей стоимости денежных потоков с течением времени, а также при оценке финансовых опционов.
- Программирование и информатика : бином Ньютона используется при разработке алгоритмов и компьютерном программировании.
Почему важен бином Ньютона?
Бином Ньютона актуален, поскольку является фундаментальным математическим инструментом для развития алгебры и теории чисел . Он позволяет вычислить результат возведения в квадрат или любую другую степень бинома, что очень полезно для решения уравнений и упрощения алгебраических выражений.
Кроме того, он находит применение в таких областях, как статистика, теория вероятности и физика . Подводя итог, можно сказать, что бином Ньютона является важным понятием в математике, и его понимание имеет решающее значение для прогресса во многих областях обучения.
Есть ли другие способы выразить бином Ньютона?
Да, есть и другие способы выразить бином Ньютона. Например, его можно выразить через биномиальные коэффициенты, используя комбинаторную запись.
Кроме того, его можно выразить через показательные функции и тригонометрические функции, используя формулу Эйлера. Аналогично с точки зрения гамма-функции по формуле Лежандра. Эти альтернативные выражения могут быть полезны в различных контекстах и математических задачах.
Биномиальные примеры Ньютона
Давайте тогда посмотрим несколько простых примеров применения бинома Ньютона.
Пример 1: Вычислите член порядка 3 в разложении (x + y) 5 .
Решение: В разложении (x + y) 5 коэффициент первого слагаемого равен 1, коэффициент второго слагаемого равен 5, коэффициент третьего слагаемого равен 10, коэффициент четвертого слагаемого равен 10, коэффициент пятого слагаемого равен 5, а коэффициент шестого слагаемого равен 1.
Таким образом, срок порядка 3 составляет:
10х 2 и 3
Пример 2: Найдите независимый член в разложении (2x – 1) 4 .
Решение: В разложении (2x – 1) 4 независимый член находится в комбинации (2x) p (-1) (4-p) , где p — значение, которое составляет показатель степени (2x) p и (-1) (4-п) в сумме получаем 4.
Таким образом, независимый термин:
(2x) 2 (-1) 2 = 4
Пример 3: Найдите член наивысшей степени в разложении (3x – 2y) 6 .
Решение: Член высшей степени в разложении (3x – 2y) 6 находится в комбинации (3x) p (-2y) (6-p) , где p — значение, которое составляет показатель степени (3x) p и (-2y) (6-p) равна степени бинома, равной 6.
Следовательно, термин высшей степени:
(3x) 3 (-2y) 3 = -216x 3 и 3