Биномы — мажность

На этой странице вы найдете объяснение того, что такое бином, а также сможете увидеть примеры каждого типа бинома. Кроме того, мы покажем вам формулы, которые используются для решения операций с биномами: умножение биномов, бином в квадрате, бином в кубе,…

Что такое пара?

В алгебре определение бинома следующее:

Бином – это многочлен, состоящий только из двух мономов . Другими словами, бином состоит из алгебраического выражения, состоящего всего из двух различных членов, соединенных знаком плюс (+) или знаком минус (-).

Слово бином происходит от греческого языка и состоит из двух лексических компонентов ( bi и nomos ), которые означают следующее:

bi : префикс, означающий 2.
номос : означает часть.

Таким образом, мы можем вывести значение бинома: многочлена из двух частей (или двух мономов).

С другой стороны, понятие пары имеет иное значение, чем математическое, а именно то, что пара может обозначать и совокупность двух личностей, которым принадлежит ведущая роль в политической жизни, в определенных спортивных дисциплинах или даже в сфере развлечений. . Но, очевидно, мы сосредоточимся здесь на математическом определении бинома.

Примеры биномов

Чтобы завершить понимание понятия бинома, мы увидим несколько примеров полинома этого типа:

Пример квадратичного бинома:

$x^2+4x$

Пример бинома третьей степени:

$x^3+5$

Пример бинома четвертой степени:

$3x^4+8x^2$

Теперь, когда мы знаем, что такое бином, мы увидим различные типы биномов, которые существуют, и способы решения операций с биномами.

бином в квадрате

Бином в квадрате — это замечательное тождество, также называемое замечательным произведением или замечательным равенством. Решение степени бинома, возведенного в 2, зависит от того, является ли он биномом суммы или биномом разности.

Биномиальная сумма относится к тому биному, два члена которого положительны, то есть бином квадратной суммы:

$(a+b)^2$

С другой стороны, бином разности (или вычитания) является сопряженным биномом сложения, то есть один из его мономов имеет отрицательный знак. Следовательно, алгебраическое выражение квадрата биномиальной разности имеет вид:

$(a-b)^2$

Чтобы вычислить квадрат бинома, необходимо применить формулу, которая, как мы видели, меняется в зависимости от того, является ли это сложением или вычитанием. Узнайте, как это делается, в формулах примечательных равенств , где вы можете увидеть все пошаговые объяснения, а также примеры и решенные упражнения, причем не только этих двух примечательных равенств, но и всех их.

биномиальный куб

Хотя кубические биномы используются реже, они также считаются примечательными продуктами. Или другими словами, существуют математические правила, позволяющие быстро найти куб бинома (их можно увидеть по ссылке выше формул заметных тождеств ).

Как и раньше, результат этого потенцирования зависит от того, является ли он кубом суммы:

$(a+b)^3$

Или, наоборот, степень представляет собой куб разности или вычитания:

$(a-b)^3$

Логично, что основная разница между биномом в квадрате и биномом в кубе — это показатель степени. Однако формула кубического бинома гораздо сложнее, чем формула квадратного бинома.

заметные соглашения

В частности, существуют определенные типы биномов, которые немного специфичны из-за своих характеристик, поскольку они соответствуют менее известным известным тождествам (или известным продуктам).

Сумма квадратов:
$a^2+b^2$
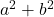
Разность (или вычитание) квадратов:
$a^2-b^2$
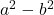
Сумма кубов:
$a^3+b^3$
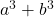
Разность (или вычитание) кубиков:
$a^3-b^3$

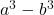
Золото

$a$

$b$

— любые два монома.

Хотя эти биномиальные выражения очень похожи на те, которые мы видели чуть выше (биномиальный квадрат и биномиальный куб), если присмотреться, они отличаются. В этом смысле вы также можете увидеть формулы примечательных биномов и их выводы, нажав на ссылку выше ⬆ формулы примечательных тождеств.⬆

биномиальное умножение

Одной из наиболее распространенных операций с биномами является умножение. Итак, далее мы увидим пример того, как вычислить умножение биномов.

$(x^2+2x)\cdot (x-5)$

Чтобы вычислить биномиальное умножение, мы должны сначала умножить каждый член первого бинома на каждый член второго бинома:

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

Далее группируем схожие термины, то есть имеющие одинаковую буквальную часть:

$\bm{x^3-3x^2 -10x}$

И таким образом нам удалось найти результат произведения между парами.

Произведение двух биномов с общим членом

Когда биномы, участвующие в умножении, имеют общим членом переменную

$x,$

Существует формула для быстрого расчета этой биномиальной операции:

$(x+a)(x+b) = x^2+(a+b)x+ab$

Здесь мы покажем вам решенное упражнение, чтобы вы увидели, как применять эту формулу:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

Бином Ньютона

Бином Ньютона , также называемый биномиальной теоремой, представляет собой формулу, используемую для вычисления степеней биномов.

Математическая формула бинома Ньютона выглядит следующим образом:

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

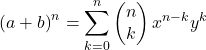
Или эквивалент:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

Как видите, эту формулу немного сложно понять. Вот почему мы привели ниже степени биномов низшей степени, чтобы вы могли лучше понять:

Эта формула может быть немного утомительной для вычисления квадратов или кубов биномов, поскольку, как мы видели выше, существуют более простые формулы. Однако бином Ньютона очень полезен для нахождения степеней более высокой степени, например, он широко используется для определения бинома четвертой степени.

Но чтобы применить эту формулу, вы должны уметь вычислять комбинаторное число, то есть алгебраическое выражение типа

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

, расчет не простой. 🔍 Именно поэтому мы рекомендуем вам поискать, как это делается, в нашей поисковой системе вверху справа 🔎, вы найдете нашу статью, где мы пошагово объясним вам эту операцию.