Абсолютная ошибка и относительная ошибка — это две меры, используемые для оценки точности расчета или оценки.
Абсолютная ошибка представляет собой разницу между фактическим значением и расчетным значением . Со своей стороны, относительная ошибка относится к отношению между абсолютной ошибкой и реальным значением.
Оба важны, поскольку предоставляют информацию о точности и актуальности результатов. Кроме того, они широко используются во многих областях, включая инженерию, физику и экономику. Мы опишем каждый ниже.
В чем абсолютная ошибка?
Абсолютная ошибка — это мера разницы между измеренным или расчетным значением и фактическим значением.
Оно представляется формулой: |измеренное значение – действительное значение| . Другими словами, абсолютная ошибка — это абсолютная величина разницы между измеренными или расчетными значениями и фактическими значениями.
Выражаясь математическим языком, оно остается следующим:
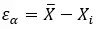
Стоит отметить, что это фундаментальное измерение во многих областях, таких как наука, технологии, инженерия и экономика, поскольку оно позволяет оценить точность результатов и качество моделей и оценок.
Как рассчитывается абсолютная ошибка?
Вычислить абсолютную ошибку просто:
Измеренное или расчетное значение вычитается из фактического значения и принимается абсолютное значение результата.
Например, если фактическое значение равно 10, а измеренное или расчетное значение равно 9, абсолютная ошибка будет равна:
|9 – 10| = |-1| = 1.
Другой пример: если фактическое значение равно 15, а измеренное или расчетное значение равно 17, абсолютная ошибка будет равна:
|17 – 15| = |2| = 2.
Вы также можете рассчитать среднюю абсолютную ошибку , которая представляет собой сумму абсолютных ошибок, деленную на количество измерений или оценок. Для его расчета необходимо следовать следующей формуле:
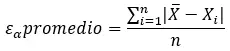
Это полезно, когда у вас много измерений или оценок и вы хотите получить общее представление о точности результатов.
Предположим, у нас есть следующие измерения или оценки:
Текущее значение: 20
Измеренное значение 1:18
Измеренное значение 2:22
Измеренное значение 3:19
Мы рассчитываем абсолютную погрешность для каждого измерения следующим образом:
Абсолютная ошибка 1: |18 – 20| = 2
Абсолютная ошибка 2: |22 – 20| = 2
Абсолютная ошибка 3: |19 – 20| = 1
Среднюю абсолютную ошибку вычисляем следующим образом: (2 + 2 + 1) ÷ 3 = 1,67. Это указывает на то, что в среднем измерения или оценки находятся в пределах 1,67 единиц от истинного значения.
Какова относительная ошибка?
Относительная ошибка — это мера точности измерения или оценки в терминах отношения абсолютной ошибки к истинному значению.
Она представлена формулой: (абсолютная ошибка) ÷ (действительное значение) . Выражаясь математическим языком, оно остается следующим:
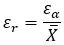
Относительная ошибка полезна для сравнения точности различных измерений или оценок, особенно когда фактические значения различны.
Как рассчитывается относительная погрешность?
При расчете относительной ошибки абсолютная ошибка нормируется , чтобы можно было сравнивать точность различных измерений или оценок независимо от их фактических значений.
Например, предположим, что у вас есть два измерения или оценки, A и B, с истинными значениями 10 и 100 соответственно и абсолютными ошибками 1 и 5 соответственно.
Относительная ошибка измерения А будет (1) ÷ (10) = (0,1), тогда как относительная ошибка измерения B будет (5) ÷ (100) = (0,05). Это указывает на то, что измерение B является более точным, чем измерение A в относительном выражении, даже несмотря на то, что оно имеет большую абсолютную ошибку.
Вот несколько примеров того, как можно рассчитать относительную ошибку:
1. Измерьте высоту здания и она составит 100 метров:
Проведя измерения, мы обнаруживаем, что на самом деле его длина составляет 98 метров.
Абсолютная ошибка составит 2 метра, а относительная ошибка будет (2) ÷ (98) = 0,0204 или 2,04%.
2. Предположим, вы хотите измерить вес объекта и подсчитали, что он весит 10 килограммов.
Сделав замеры, мы обнаружили, что на самом деле он весит 9,5 килограмма.
Абсолютная ошибка составит 0,5 килограмма, а относительная ошибка будет (0,5) ÷ (9,5) = 0,0526 или 5,26%.
3. Предположим, вы хотите измерить длину доски, и она оценивается в 200 сантиметров.
Проведя измерения, мы обнаруживаем, что на самом деле он составляет 201 сантиметр.
Абсолютная ошибка составит 1 сантиметр, а относительная ошибка будет (1) ÷ (201) = 0,00498 или 0,498%.
В каждом из этих примеров относительная ошибка представляет собой меру точности измерения с точки зрения отношения абсолютной ошибки к истинному значению. Это позволяет сравнивать точность различных измерений и оценок независимо от их фактических значений.
В чем разница между абсолютной ошибкой и относительной ошибкой?
Абсолютная ошибка и относительная ошибка — это две разные меры оценки точности результата или модели.
Абсолютная ошибка относится к разнице между фактическим или истинным значением величины и расчетным или измеренным значением. Ее можно рассчитать как разницу между фактической стоимостью и расчетной стоимостью:
Абсолютная погрешность = фактическое значение – расчетное значение
Абсолютная ошибка может быть положительной или отрицательной в зависимости от того, больше или меньше оценочное значение истинного значения.
С другой стороны, относительная ошибка относится к взаимосвязи между абсолютной ошибкой и реальным или истинным значением . Его можно рассчитать как долю абсолютной ошибки и истинного значения:
Относительная ошибка = абсолютная ошибка ÷ фактическое значение
Относительная ошибка обычно выражается в процентах . Этот тип ошибок позволяет сравнивать точность разных результатов или моделей независимо от их величины.
Например, абсолютная ошибка 1,0 может быть значительным отклонением на небольшую величину, но не на большую величину. Однако относительная погрешность в обоих случаях будет одинаковой.
Короче говоря, абсолютная ошибка измеряет разницу между фактической стоимостью и расчетной стоимостью, тогда как относительная ошибка измеряет точность оценки с точки зрения ее отношения к фактическому значению.
Каковы применения абсолютной ошибки и относительной ошибки?
Абсолютная и относительная погрешности имеют широкий спектр применения в различных областях, в том числе:
- Наука – в научных экспериментах для оценки точности измерений и качества результатов.
- Технология – Производство и контроль качества для оценки точности машин и оборудования.
- Инжиниринг – строительство и проектирование для оценки точности измерений и обеспечения качества готовой продукции.
- Экономика : оценка активов и оценка финансовых рисков для оценки точности прогнозов и принятия обоснованных решений.
- Математика и статистика : моделирование и оценка для оценки точности результатов и улучшения моделей.
Примеры расчета абсолютной и относительной ошибки
Вот два простых примера для расчета как абсолютной, так и относительной ошибки:
1. Предположим, что вес объекта оценивается в 3,0 кг, а его фактический вес составляет 2,8 кг.
Абсолютную погрешность рассчитываем следующим образом:
Абсолютная погрешность = фактическое значение – расчетное значение = 2,8 кг – 3,0 кг = -0,2 кг
Относительную погрешность рассчитываем следующим образом:
Относительная погрешность = Абсолютная погрешность ÷ Фактическое значение = -0,2 кг ÷ 2,8 кг = -0,0714 или -7,14%
2. Предположим, что объем контейнера оценивается в 50 литров, а его фактический объем составляет 45 литров.
Абсолютную погрешность рассчитываем следующим образом:
Абсолютная погрешность = фактическое значение – расчетное значение = 45 литров – 50 литров = -5 литров
Относительную погрешность рассчитываем следующим образом:
Относительная погрешность = Абсолютная погрешность ÷ Фактическое значение = -5 литров ÷ 45 литров = -0,1111 или -11,11%
3. Предположим, что население города оценивается в 1 миллион человек, а фактическая численность составляет 975 000 человек.
Абсолютную погрешность рассчитываем следующим образом:
Абсолютная ошибка = фактическое значение – расчетное значение = 975 000 – 1 000 000 = -25 000
Относительную погрешность рассчитываем следующим образом:
Относительная ошибка = Абсолютная ошибка ÷ Фактическое значение = -25 000 ÷ 975 000 = -0,0257 или -2,57 %.
4. Предположим, что площадь футбольного поля оценивается в 10 000 квадратных метров, а фактическая площадь — 9 900 квадратных метров.
Абсолютную погрешность рассчитываем следующим образом:
Абсолютная погрешность = фактическое значение – расчетное значение = 9 900 – 10 000 = -100 квадратных метров.
Относительную погрешность рассчитываем следующим образом:
Относительная ошибка = Абсолютная ошибка ÷ Фактическое значение = -100 ÷ 9900 = -0,0101 или -1,01%
В этих примерах абсолютная и относительная ошибки говорят нам о точности оценки. Абсолютная ошибка говорит нам, насколько оценка отклонилась от истинного значения, тогда как относительная ошибка говорит нам, насколько оценка отклонилась с точки зрения ее отношения к истинному значению.