Эрмитова (или эрмитова) матрица

На этой странице вы можете узнать, что такое эрмитова матрица, также известная как эрмитова матрица. Вы найдете примеры эрмитовых матриц, все их свойства и форму, которую имеют эти типы матриц, чтобы понять их в совершенстве. Наконец, мы также объясним, как разложить любую комплексную матрицу на сумму эрмитовой матрицы и антиэрмитовой матрицы.

Что такое эрмитова или эрмитова матрица?

Эрмитова матрица , или также называемая эрмитовой матрицей, представляет собой квадратную матрицу с комплексными числами, которая имеет характеристику, равную ее сопряженному транспонированию .

$A=A^*$

Золото

$A^*$

— сопряженная транспонированная матрица

$A$

Из любопытства этот тип матрицы назван в честь Шарля Эрмита, французского математика XIX века, который провел важные исследования в области математики, особенно в области линейной алгебры.

Причиной такого названия этой матрицы было то, что она показала, что собственные значения (или собственные значения) этих конкретных матриц всегда являются действительными числами, но мы объясним это более подробно в разделе «Свойства эрмитовых матриц».

Наконец, эту матрицу иногда также можно назвать самосопряженной, хотя это происходит очень редко.

Примеры эрмитовых матриц

После того, как мы увидели определение эрмитовой матрицы (или эрмитовой матрицы), давайте посмотрим несколько примеров эрмитовых матриц разных размерностей:

Пример эрмитовой матрицы порядка 2×2

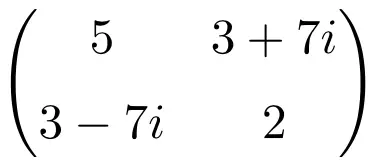
Эрмитова или эрмитова матрица размерности 2х2.

Пример эрмитовой матрицы размерности 3 × 3

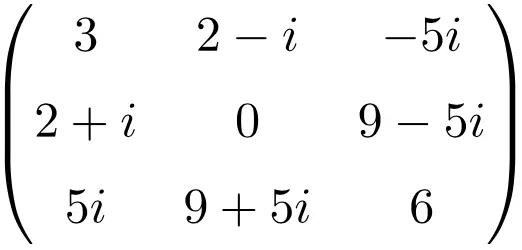
Эрмитова или эрмитова матрица размерности 3х3.

Пример эрмитовой матрицы размером 4×4

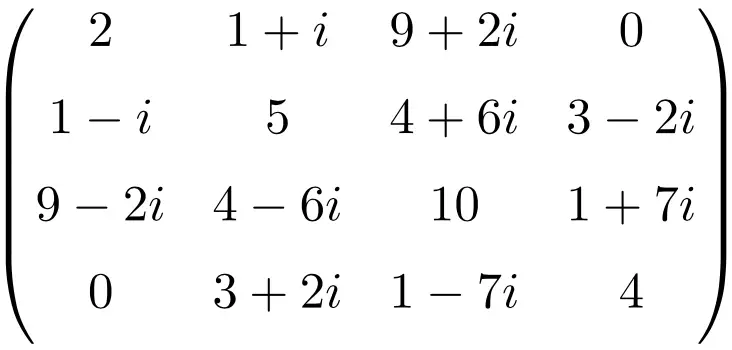
Эрмитова или эрмитова матрица размерности 4х4.

Все эти матрицы являются эрмитовыми, поскольку сопряженная транспонированная матрица каждой равна самой матрице.

Структура эрмитовой матрицы

Эрмитовы матрицы имеют очень легко запоминающуюся структуру: они составлены из вещественных чисел на главной диагонали, причем комплексный элемент, расположенный в i-й строке и j-м столбце, должен быть сопряженным элементу, найденному в j-й строке и i-й столбец.

Вот несколько примеров эрмитовых матричных структур.

Эрмитова структура 2×2

$\displaystyle \begin{pmatrix}a& b\\[1.1ex] \overline{b} & c \end{pmatrix}$

Эрмитова структура 3×3

$\displaystyle \begin{pmatrix}a& b & c \\[1.1ex] \overline{b} & d & e \\[1.1ex] \overline{c} & \overline{e} & f\end{pmatrix}$

Эрмитова структура 4×4

$\displaystyle \begin{pmatrix}a& b & c & d \\[1.1ex] \overline{b} & e & f & g \\[1.1ex] \overline{c} & \overline{f} & h & i \\[1.1ex] \overline{d} & \overline{g} & \overline{i} & j \end{pmatrix}$

Свойства эрмитовой матрицы

Теперь мы увидим, каковы свойства этого типа квадратной комплексной матрицы:

Любая эрмитова матрица является нормальной матрицей . Хотя не все нормальные матрицы являются эрмитовыми.

Любая эрмитова матрица диагонализуема. Более того, полученная диагональная матрица содержит только вещественные элементы.

Следовательно, собственные значения (или собственные значения) эрмитовой матрицы всегда являются действительными числами. Это свойство было открыто Чарльзом Эрмитом, и по этой причине он удостоился чести назвать эту особенную матрицу Эрмитовой.

Аналогично, собственные пространства эрмитовой матрицы ортогональны два на два: существует ортонормированный базис
$\mathbb{C}^n$

состоящая из собственных векторов (собственных векторов) матрицы.

Матрица действительных чисел, то есть ни один элемент не имеет мнимой части, является эрмитовой тогда и только тогда, когда она является симметричной матрицей. Как, например , единичная матрица 2×2 .

Эрмитова матрица может быть выражена как сумма действительной симметричной матрицы и мнимой антисимметричной матрицы .

$A =B+Ci$

Сумма (или вычитание) двух эрмитовых матриц равна другой эрмитовой матрице, потому что:

$(A\pm B)^* = A^*\pm B^* = A \pm B$

Результатом произведения эрмитовой матрицы на скаляр является другая эрмитова матрица, если скаляр является действительным числом.

$(k \cdot A)^* = \overline{k}\cdot A^* = k \cdot A$

Произведение двух эрмитовых матриц, как правило, уже не является эрмитовым. Однако произведение является эрмитовым, когда две матрицы коммутативны, то есть когда результат умножения двух матриц один и тот же независимо от направления их умножения, поскольку тогда выполняется следующее условие операций с сопряженным транспонированием матрицы:

$(A \cdot B)^* = B^*\cdot A^* = B \cdot A = A \cdot B$

Если эрмитова матрица обратима, то ее обратная также оказывается эрмитовой матрицей.

$(A^{-1})^* = (A^*)^{-1} = A^{-1}$

Определитель эрмитовой матрицы всегда эквивалентен действительному числу. Вот доказательство этого свойства:

$det(A) = det(A^t) \ \longrightarrow \ det(A^*) = \overline{det(A)}$

Испытывающий жажду

$A = A^*$

$det(A) = \overline{det(A)}$

Следовательно, чтобы это условие выполнялось, определитель эрмитовой матрицы обязательно должен быть действительным числом. Таким образом, сопряженное результат равно самому результату.

Разложение комплексной матрицы на эрмитову матрицу и антиэрмитову матрицу

Любую матрицу с комплексными элементами можно разложить на сумму эрмитовой матрицы и другой антиэрмитовой матрицы . Но для этого необходимо знать следующие особенности этих типов матриц:

Сумма квадратной комплексной матрицы плюс ее транспонированная сопряженная матрица дает эрмитову матрицу.

$C + C^* = \text{Matriz Hermitiana}$

Разница между квадратной комплексной матрицей и ее транспонированной сопряженной матрицей дает антиэрмитову (или антиэрмитову) матрицу.

$C - C^* = \text{Matriz Antihermitiana}$

Следовательно, все комплексные матрицы можно разложить в сумму эрмитовой и антиэрмитовой матриц. Эта теорема известна как разложение Теоплица :

$\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}$

Где C — комплексная матрица, которую мы хотим разложить, C* — ее транспонированная сопряженная матрица, и, наконец, A и B — соответственно эрмитова и антиэрмитова матрицы, на которые разлагается матрица C.

Что такое эрмитова или эрмитова матрица?

Примеры эрмитовых матриц

Структура эрмитовой матрицы

Свойства эрмитовой матрицы

Разложение комплексной матрицы на эрмитову матрицу и антиэрмитову матрицу

Оставьте комментарий Отменить ответ