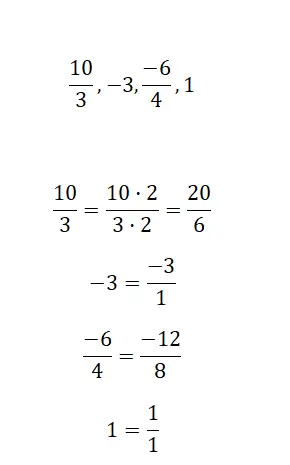В этой статье вы найдете очень полное и легкое для понимания объяснение эквивалентных дробей или равных дробей . Более конкретно мы поговорим об их определении, о том, как их вычислить и как узнать, эквивалентны ли две дроби. Таким образом, вы будете знать все, что вам нужно для решения упражнений на эквивалентные дроби, подобных тем, которые мы представим вам в конце. Тем не менее, давайте начнем с темы.
Калькулятор эквивалентных дробей
С помощью этого калькулятора эквивалентных дробей вы сможете проверить, равны ли две дроби, без необходимости выполнять какие-либо вычисления. Его работа очень проста: вам нужно ввести значения, соответствующие двум числителям и двум знаменателям, и нажать кнопку «Рассчитать».
Что такое эквивалентные дроби?
Эквивалентные дроби — это те, которые выражают одно и то же числовое значение , следовательно, это дроби, эквивалентные одному и тому же результату, даже если они имеют разные числитель и знаменатель. Это означает, что между ними существует пропорциональная связь, которая может быть двух типов: усиленная или упрощенная. Далее мы покажем вам наглядный пример эквивалентных дробей, чтобы лучше понять концепцию.
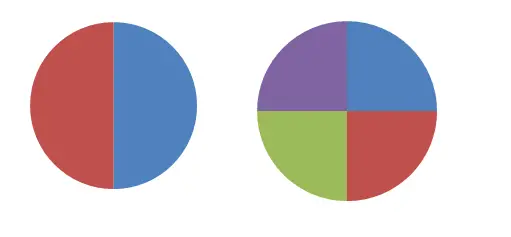
На предыдущем изображении вы можете увидеть два круга, разделенные на две и четыре части. Если мы попытаемся определить первую дробью, то скажем, что каждая часть равна 1/2 целого, тогда как на втором рисунке мы будем использовать дробь 1/4. Очевидно, что эти две дроби не эквивалентны , так как представляют собой разные величины. Но, если взять две части второго круга (2/4), то это выражение эквивалентно 1/2.
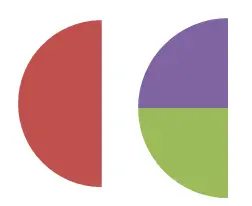
На этом втором изображении вы можете увидеть эквивалентность между 1/2 и 2/4 , которую также можно проверить численно. Так как 1/2 = 0,5 и 2/4 = 0,5. Согласно определению, которое мы прокомментировали ранее, если две дроби выражают одно и то же числовое значение, то они являются эквивалентными дробями.
Примеры эквивалентных дробей
Сейчас мы покажем вам 5 примеров эквивалентных дробей. И если вы хотите понять, как мы их рассчитали, рекомендуем продолжить чтение.
- Дроби, эквивалентные половине: 2/4, 3/6, 4/8 и т.д.
- Дроби, эквивалентные трети: 2/6, 3/9, 4/12 и т.д.
- Дроби, эквивалентные четверти: 2/8, 3/12, 4/16 и т.д.
- Дроби, равные единице: 4/4, 7/7, 15/15 и т.д.
- Дроби, эквивалентные пятой части: 2/10, 3/15, 4/20 и т.д.
Как вычислить эквивалентные дроби?
Чтобы получить эквивалентные дроби, нам нужно умножить или разделить числитель и знаменатель на одно и то же число. Так как, если мы изменяем обе части дроби одинаково, мы сохраняем пропорциональную связь. Поэтому мы можем использовать два метода: усиление и уменьшение.
Нахождение эквивалентной дроби путем амплификации
В этом первом случае нам нужно умножить исходную дробь на определенное числовое значение. Это означает, что нам нужно умножить числитель и знаменатель на это число. Чтобы вы могли убедиться в этом на примере, ниже мы покажем вам две равнозначные дроби, которые получаются после умножения:
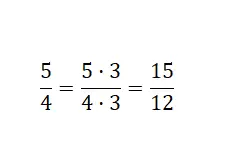
Мы умножили обе части дроби на три: 5 х 3 = 15 и 4 х 3 = 12 . Таким образом, мы получаем усиленную эквивалентную фракцию, поскольку она больше. В заключение мы нашли дробь, состоящую из разных числовых значений, которая выражает ту же величину, что и исходная дробь.
Нахождение эквивалентной дроби упрощением
Во-вторых, мы можем упростить дробь , разделив числитель и знаменатель данной дроби. Таким образом мы получим еще одну эквивалентную дробь , еще более простую, чем первая. Однако стоит отметить, что этот метод работает только в том случае, если исходное выражение не является неприводимой дробью , так как последнюю невозможно сократить дальше. Ниже приведен пример расчета эквивалентной дроби путем сокращения (упрощения).
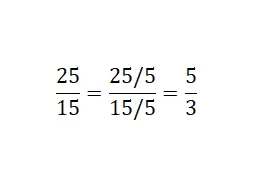
Как вы можете видеть на рисунке, мы разделили числитель и знаменатель дроби на общий делитель . В этом примере мы использовали пять: 25/5 = 5 и 15/5 = 3. Наконец, мы получили несократимую эквивалентную дробь 25/15.
Как узнать, эквивалентны ли две дроби?
Чтобы определить эквивалентные дроби, мы должны выполнить одну из трех процедур, которые мы объясним ниже. Следует отметить, что второе связано с упрощением дробей, о котором мы говорили в предыдущем разделе.
Умножение числителей на знаменатели
Если вы хотите проверить эквивалентность двух дробей, вы можете использовать первую процедуру. По сути, вам нужно умножить числитель первой дроби на знаменатель второй. Далее нужно числитель второй дроби умножить на знаменатель первой. Если оба результата дают одинаковое значение , то эти дроби будут эквивалентны. Посмотрите на следующий пример:
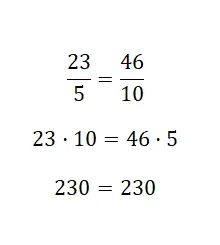
В этом последнем примере мы проверили, что две дроби эквивалентны. Этот пример было легко увидеть, поскольку вторая дробь вдвое больше первой, то есть они имеют усиленное отношение эквивалентности . Следует отметить, что данная процедура довольно удобна в использовании, достаточно просто перемножить крестики. Но мы также рекомендуем вам научиться использовать две другие системы, поскольку это предоставит вам больше математических ресурсов.
Упростить дроби
Когда дело доходит до несократимых дробей , мы можем использовать другой метод, который заключается в максимально возможном сокращении дроби, состоящей из наибольших чисел. Если при этом сокращении мы обнаружим, что меньшая дробь является несократимой другой, то можно предположить, что они эквивалентны.
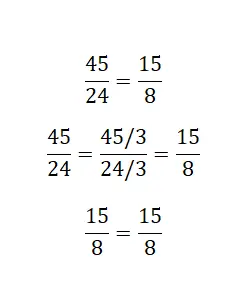
Разрешить и уравнять разделения
Наконец, вы можете прибегнуть к частному решению , полученному по дробям, поскольку смешанное число всегда является делением. По сути, вам нужно вычислить эквивалентное числовое значение двух дробей, и если это одно и то же число, то они будут эквивалентны. На следующем изображении вы можете увидеть очень наглядный пример:
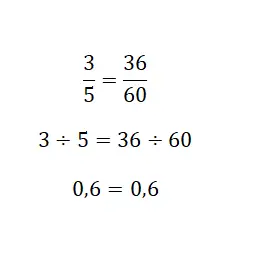
Упражнения на эквивалентные дроби
Теперь, когда вы прочитали всю теорию, вы можете попробовать решить следующие упражнения, которые позволят вам до конца понять объяснение. Мы рекомендуем вам попробовать решить их самостоятельно и, как только они у вас появятся, сравнить свой результат с тем, который мы вам предлагаем. Тем не менее, мы позволяем вам практиковаться:
Упражнение 1
Найдите эквивалентную дробь путем упрощения для каждой предлагаемой нами дроби:
Чтобы решить это упражнение, просто примените упрощение дробей, получив таким образом эквивалентную несократимую дробь. Четыре примера очень похожи, поэтому особых сложностей в их решении не возникает.
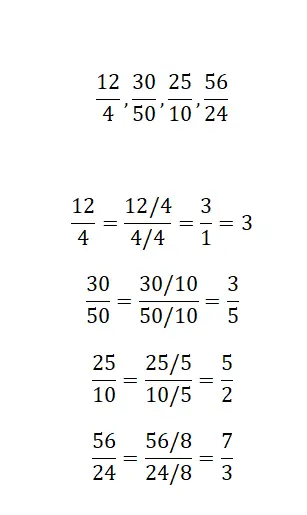
Упражнение 2
Найдите эквивалентную фракцию путем амплификации для каждой предложенной нами фракции:
Далее вам придется амплифицировать предложенные нами дроби, таким образом вы получите более крупные эквивалентные дроби. Неважно, какое число вы используете для умножения, например, мы сделаем это с 2 и 3.
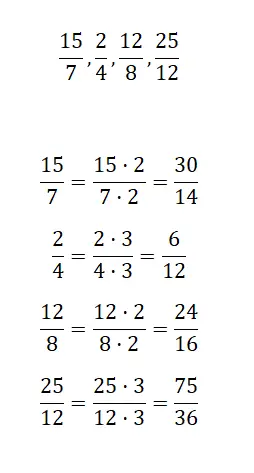
Упражнение 3
Определите, эквивалентны ли следующие дроби:
Чтобы узнать, эквивалентны ли две дроби, вам нужно использовать один из трех методов, которые мы объяснили выше. Вы найдете исправления, решенные с помощью первой процедуры, хотя вы можете использовать любую систему, которую захотите.
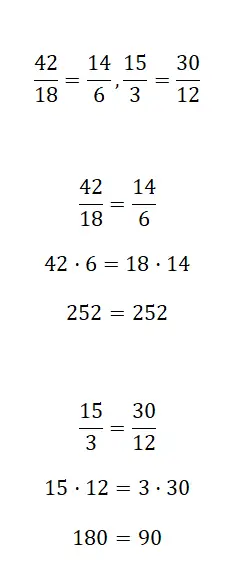
Упражнение 4
Вычислите эквивалентные дроби следующих выражений:
В этом последнем упражнении вам придется переписать предложенные нами выражения ( целые числа и смешанные числа) в виде дробей, стараясь сохранить отношения эквивалентности.