На этой странице вы найдете объяснение того, что представляют собой компоненты (или координаты) вектора. Также вы сможете увидеть, как они рассчитываются по двум точкам и даже как они разлагаются по модулю и углу. Кроме того, вы найдете примеры и упражнения, решаемые шаг за шагом.
Каковы компоненты вектора?
Компоненты вектора — это проекции вектора на декартовы оси. Следовательно, проекция вектора на ось x является компонентом X вектора и, аналогично, проекция вектора на ось y является компонентом Y вектора.
Компоненты вектора также можно назвать координатами вектора.
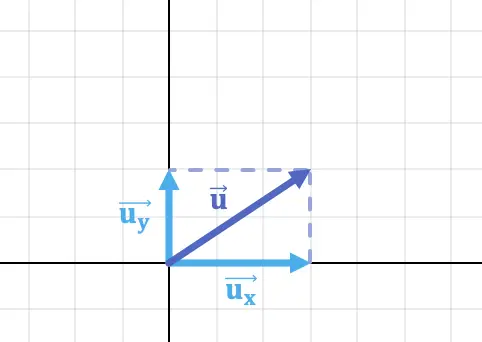
Например, горизонтальный компонент и вертикальный компонент вектора на изображении выше:
![]()
![]()
Итак, вектор:
![]()
Следовательно, компоненты вектора также можно определить как представление вектора в системе координат. Очевидно, что если это двумерная система (в г2), то вектор будет состоять из двух компонент, с другой стороны, если это трехмерная база (в г3), вектор будет состоять из трех компонент.
Декартовы компоненты вектора так важны, потому что с их помощью мы можем узнать характеристики вектора, которыми в основном являются направление, смысл и модуль (или величина) вектора. Кроме того, они используются для выполнения векторных операций.
Как вычислить компоненты вектора по двум точкам
Мы только что увидели, как найти координаты вектора графически, однако его компоненты можно определить и численно.
Чтобы численно рассчитать компоненты вектора, нам необходимо знать две точки: его начало и конец, или другими словами, где он начинается и где заканчивается. Поскольку компоненты вектора — это координаты, которые мы получаем, вычитая его конец минус начало координат.
![]()
Например, мы вычислим вектор, начало которого — точка A(3,1), а конец — точка B(5,4):
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{AB} & = (5,4)-(3,1) \\[1.5ex] &= (5-3,4-1) \\[1.5ex] & = \bm{(2,3)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c740536015a29149532a4a1eb46f4f7_l3.png)
Как видите, определить компоненты вектора не очень сложно, однако это достаточно важно. Например, одним из наиболее часто используемых типов векторов являются перпендикулярные (или ортогональные) векторы; Что ж, если вы понимаете, что такое координаты вектора, вычислить перпендикулярные векторы очень легко. Вы можете увидеть, как это делается, в объяснении ортогональных векторов .
Как вычислить компоненты вектора по его модулю и углу
Вы также можете найти компоненты вектора по его величине и углу, который он составляет с осью X. Этот процесс называется векторной декомпозицией .
Таким образом, компоненты вектора X и Y можно вычислить с помощью тригонометрических отношений косинуса и синуса:

Как вы можете видеть на изображении, модуль вектора и его компоненты образуют прямоугольный треугольник, поэтому можно применить элементарные формулы тригонометрии.
Если вы не помните, как рассчитывается модуль вектора, вы можете узнать , что такое модуль вектора . Здесь вы найдете формулу величины вектора, а также примеры, пошагово решаемые упражнения и все свойства величины вектора. Это очень полное объяснение, поэтому вы его прекрасно поймете. ✅
В отличие от величины вектора, которая всегда положительна, его компоненты могут быть отрицательными, поскольку синус и косинус могут принимать отрицательные значения.
В качестве примера сделаем векторное разложение вектора, модуль и угол которого с осью OX равны:
![]()
X-компонента вектора равна модулю, умноженному на косинус угла:
![]()
А составляющая Y вектора равна произведению модуля и синуса угла:
![]()
Итак, координаты вектора:
![]()