Здесь вы узнаете, что такое функция идентификации. Кроме того, вы сможете увидеть, как графически представить функцию тождества и каковы ее характеристики.
Что такое функция идентичности?
Функция идентичности — это функция, изображение которой имеет то же значение, что и аргумент. Функция идентичности может быть выражена с помощью термина id .
Следовательно, математическое выражение тождественной функции имеет вид:
![]()
Например, образ тождественной функции для x=1 стоит 1, образ x=2 стоит 2, образ x=3 стоит 3,…
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
Функция тождества является примером линейной функции. По следующей ссылке вы можете увидеть больше примеров функций этого типа:
➤ См.: примеры линейных функций
Графическое представление функции идентичности
График тождественной функции соответствует линии, которая является биссектрисой первого и третьего квадрантов.
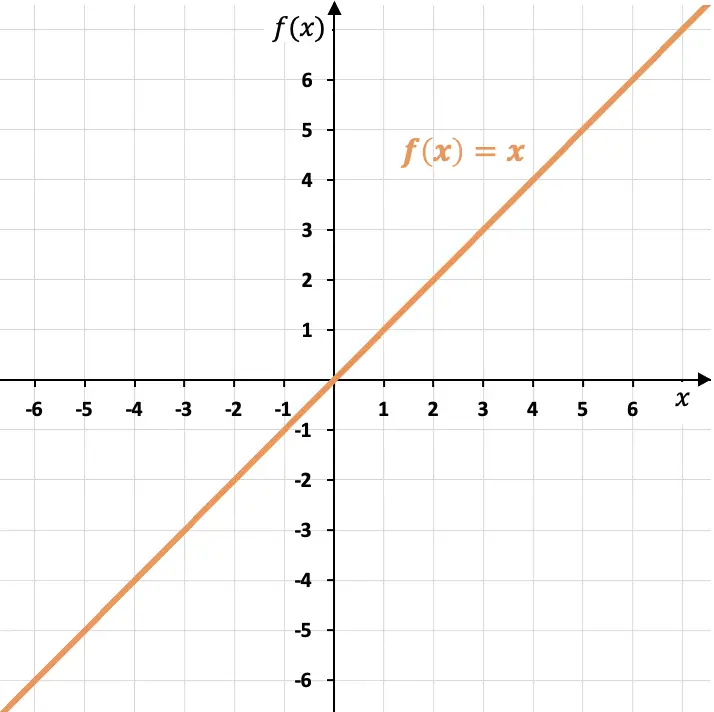
Как видим, тождественная функция проходит через начало координат (точку (0,0)) и имеет наклон, равный единице (m=1), так как увеличивается одна единица переменной и для каждого значения независимой переменная X. Кроме того, функция идентичности образует угол 45° с осью X.
Характеристики функции идентичности
Функция тождества имеет следующие свойства:
- Областью определения тождественной функции являются все действительные числа:
![]()
- Диапазон (или диапазон) тождественной функции также состоит из всех действительных чисел:
![]()
- Функция тождества является непрерывной и биективной функцией.
- Кроме того, тождественная функция состоит из нечетной функции, что означает, что она является симметричной функцией относительно начала координат.
![]()
➤ См.: нечетная симметричная функция.
- Тождественная функция возрастает во всей своей области определения, а ее наклон равен 1.
![]()
- Пересекает ось X (ось OX) и ось Y (ось Y) в одной и той же точке: начале координат.
![]()
- Ее можно классифицировать как полиномиальную функцию первой степени.
- Функция идентичности действует как нейтральный элемент композиции функций . Таким образом, любая функция, составленная с помощью тождественной функции, приводит к самой функции.
![]()
- Значение
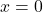
является единственным корнем функции этого типа.
- Предел тождественной функции, когда x стремится к плюс бесконечности или минус бесконечности, дает соответственно плюс бесконечность и минус бесконечность:
![]()
![]()
- Таким образом, тождественная функция не имеет асимптоты.
- Производная тождественной функции — это постоянная функция со значением 1:
![]()
- Интеграл от тождественной функции представляет собой квадратичную функцию:
![]()
➤ См.: формула квадратичной функции