Формула расстояния между двумя точками (геометрия)

На этой странице вы узнаете, как рассчитать расстояние между двумя точками в геометрии (формула). Вы также сможете посмотреть примеры и дополнительно потренироваться на решенных упражнениях на расстояние между двумя точками.

По какой формуле определяется расстояние между двумя точками?

Расстояние между двумя точками равно длине соединяющего их отрезка. Поэтому в математике, чтобы определить расстояние между двумя разными точками, мы должны вычислить квадраты разностей их координат, а затем найти корень из суммы указанных квадратов.

Другими словами, формула, используемая для расчета расстояния между двумя разными точками на декартовой плоскости, выглядит следующим образом:

Рассмотрим координаты двух различных точек:

$A(x_1,y_1) \qquad \qquad B(x_2,y_2)$

Формула расстояния между двумя точками :

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Эта формула исходит из величины вектора. Фактически, то, что мы делаем с этой формулой, на самом деле вычисляем величину вектора, который определяется двумя рассматриваемыми точками. Подробнее об этом можно прочитать в объяснении того, что такое модуль вектора .

С другой стороны, в аналитической геометрии демонстрацию формулы расстояния между двумя точками можно провести и с помощью теоремы Пифагора:

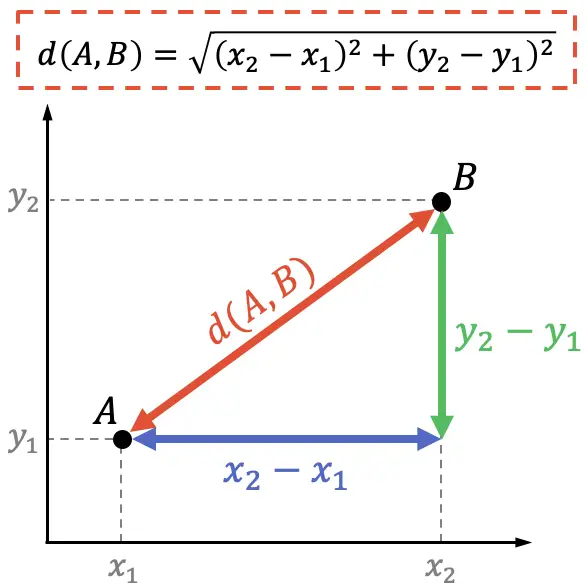
Теорема Пифагора утверждает, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов, следовательно:

$\bigl(d(A,B)\bigr)^2 = (x_2-x_1)^2 + (y_2-y_1)^2$

И чтобы получить формулу, вам просто нужно найти расстояние между двумя точками:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Наконец, стоит отметить, что если бы мы работали с 3-координатными точками, формула расстояния между двумя точками в пространстве (в R3) была бы такой же, но с добавлением координаты Z:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2 \vphantom{\frac{1}{2}}}$

Пример расчета расстояния между двумя точками

После того, как мы увидели определение формулы расстояния между двумя точками, давайте теперь посмотрим, как определить это расстояние на примере:

Найдите расстояние между следующими двумя точками:

$A(-1,7) \qquad \qquad B(3,4)$

Чтобы геометрически найти расстояние между двумя точками, просто примените формулу:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Теперь подставляем координаты точек в формулу:

$d(A,B) = \sqrt{(3-(-1))^2+(4-7)^2 \vphantom{\frac{1}{2}}}$

И делаем расчеты:

$\begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}$

Следовательно, расстояние между двумя точками равно 5 единицам.

Очевидно, что значение расстояния всегда должно давать нам положительный знак, потому что расстояния всегда положительны. В противном случае это означает, что мы допустили ошибку на шаге.

Устранение неполадок с расстоянием между двумя точками

Упражнение 1

Рассчитайте расстояние между следующими двумя точками:

$A(4,2) \qquad \qquad B(1,5)$

посмотреть решение

Чтобы найти геометрическое расстояние между двумя точками, просто используйте формулу:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Теперь подставляем координаты точек в формулу:

$d(A,B) = \sqrt{(1-4)^2+(5-2)^2 \vphantom{\frac{1}{2}}}$

И делаем расчеты:

$\begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}$

Упражнение 2

Найдите расстояние между следующими двумя точками:

$A(8,6) \qquad \qquad B(-4,1)$

посмотреть решение

Чтобы найти математическое расстояние между двумя точками, мы должны использовать соответствующую формулу:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Теперь подставляем координаты точек в формулу:

$d(A,B) = \sqrt{(-4-8)^2+(1-6)^2 \vphantom{\frac{1}{2}}}$

И делаем расчеты:

$\begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}$

Упражнение 3

Вычислите периметр треугольника, образованного точками A, B и C, показанными на графике ниже:

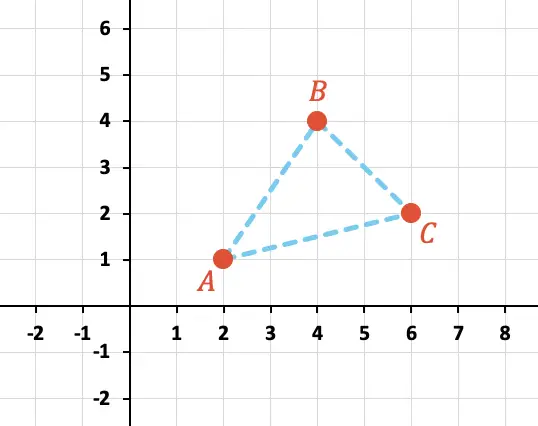
решено упражнение на расстояние между двумя точками

посмотреть решение

Во-первых, нам нужно определить координаты X и Y каждой точки на графике:

$A(2,1)$

$B(4,4)$

$C(6,2)$

И теперь нам нужно вычислить расстояние между всеми точками по формуле:

$d(A,B) = \sqrt{(4-2)^2+(4-1)^2 } = \sqrt{4+9} =\sqrt{13} = 3,61$

$d(A,C) = \sqrt{(6-2)^2+(2-1)^2 } = \sqrt{16+1} =\sqrt{17} = 4,12$

$d(B,C) = \sqrt{(6-4)^2+(2-4)^2 } = \sqrt{4+4} =\sqrt{8} = 2,83$

Значит периметр треугольника будет равен сумме длин трёх сторон:

$P=3,61+4,12+2,83= \bm{10,56}$

Упражнение 4

Проверьте, является ли треугольник, вершинами которого являются точки A, B и C, равнобедренным. Но три пункта:

$A(-4,5) \qquad B(7,-5) \qquad C(10,0)$

посмотреть решение

Чтобы треугольник был равнобедренным, необходимо, чтобы две его стороны были равны. Поэтому мы должны найти длину каждой из его сторон, которая соответствует расстоянию между его вершинами.

Поэтому мы вычисляем расстояние между вершинами треугольника:

$d(A,B) = \sqrt{(7-(-4))^2+(-5-5)^2 } = \sqrt{11^2+(-10)^2} = \sqrt{221}$

$d(A,C) = \sqrt{(10-(-4))^2+(0-5)^2 } = \sqrt{14^2+(-5)^2} = \sqrt{221}$

$d(B,C) = \sqrt{(10-7)^2+(0-(-5))^2} = \sqrt{3^2+5^2} = \sqrt{34}$

Таким образом, у треугольника две одинаковые стороны, а размеры третьей стороны отличаются от двух других, то это фактически равнобедренный треугольник.

Упражнение 5

Найдите точку на оси Y, которая находится на равном расстоянии от следующих двух точек:

$A(5,-3) \qquad \qquad B(-2,4)$

посмотреть решение

Прежде всего, если точка расположена на оси компьютера (ось OY), это означает, что абсцисса точки равна нулю:

$P(0,y)$

Во-вторых, если точка равноудалена от точек A и B, это означает, что выполняется следующее уравнение:

$d(P,A)= d(P,B)$

Итак, используя формулу расстояния между двумя точками, мы можем найти значение переменной y из предыдущего уравнения:

$\sqrt{(5-0)^2+(-3-y)^2 \vphantom{\frac{1}{2}}}=\sqrt{(-2-0)^2+(4-y)^2 \vphantom{\frac{1}{2}}}$

Поскольку обе части уравнения имеют корень, мы можем их упростить:

$5^2+(-3-y)^2=(-2)^2+(4-y)^2$

Решаем известные степени и равенства (или известные произведения):

$25+9+y^2+6y=4+16+y^2-8y$

И действуем до тех пор, пока не найдём значение неизвестного y :

$y^2+6y-y^2+8y=4+16-25-9$

$14y=-14$

$y=\cfrac{-14}{14}$

$y=-1$

Короче говоря, суть постановки задачи заключается в следующем:

$\bm{P(0,-1)}$

Если эта статья оказалась для вас полезной, возможно, вас также заинтересуют упражнения на расстояние между точкой и прямой . На связанной странице вы найдете не только пошагово решенные упражнения, но и подробное объяснение расчета расстояния между точками и линиями, примеры и применение формулы расстояния между точкой и линией для определения другого вида расстояния. .

По какой формуле определяется расстояние между двумя точками?

Пример расчета расстояния между двумя точками

Устранение неполадок с расстоянием между двумя точками

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Оставьте комментарий Отменить ответ