Унитарная матрица

На этой странице мы объясняем, что такое унитарная матрица, и, кроме того, иллюстрируем ее несколькими упражнениями, чтобы она была хорошо понята. Вы также узнаете, каковы свойства этого типа матрицы, столь важные для линейной алгебры.

Что такое унитарная матрица?

Определение унитарной матрицы следующее:

Унитарная матрица — это комплексная матрица, умноженная на сопряженную ей транспонированную матрицу, равную единичной матрице. То есть выполняется следующее условие:

U\cdot U^* = U^* \cdot U =I

Золото

U

является унитарной матрицей и

U^*

его сопряженное транспонирование.

Следовательно, из этого условия следует, что обратная единичной матрице является ее сопряженной транспонированием , поскольку по определению обратной матрицы матрица является обратной матрицей другой, если ее произведение эквивалентно матрице d’identify .

\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}

Следовательно, унитарная матрица всегда будет регулярной или невырожденной матрицей , поскольку она всегда будет иметь обратную.

С другой стороны, аналогом унитарной матрицы в среде действительных чисел является ортогональная матрица , и в этом случае верно, что унитарная матрица, умноженная на ее транспонирование, равна единичной матрице.

U\cdot U^t = U^t \cdot U =I

Таким образом, в этом случае обратная матрица U будет непосредственно ее транспонированной (или транспонированной) матрицей.

Примеры единичных матриц

Пример единичной матрицы размерности 2×2

Как только мы познакомимся с концепцией единичной матрицы, мы увидим пример единичной матрицы 2×2, чтобы лучше ее понять:

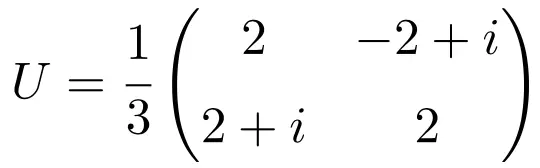
пример единичной матрицы размером 2x2

Эта матрица является унитарной, поскольку умножение самой себя на сопряженную матрицу дает матрицу идентичности (или единицы измерения):

\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

И, как мы видели ранее, любая унитарная матрица коммутабельна с сопряженным ей транспонированием:

\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

Пример единичной диагональной матрицы

Диагональная матрица , состоящая только из комплексного числа i , также является примером унитарной матрицы, независимо от ее размерности. Ниже вы найдете решенное упражнение, иллюстрирующее это с помощью единичной матрицы размером 3 × 3:

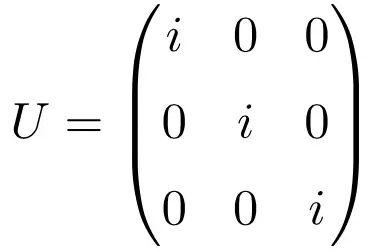
пример единичной матрицы размером 3x3

Обратите внимание: если мы решим произведение матрицы путем ее сопряженного транспонирования, это даст матрицу идентичности в качестве решения:

\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

И то же самое произойдет, если мы перемножим матрицы в обратном порядке:

\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

Характеристика этой матрицы состоит в том, что она служит примером унитарной матрицы любой размерности, поскольку каждый раз матрица формируется мнимым числом i на главной диагонали, а остальные элементы равны нулю (0 ) это будет унитарная матрица.

Свойства унитарной матрицы

Свойства единичных матриц следующие:

  • Очевидно, что любая унитарная матрица является нормальной матрицей . Хотя не все нормальные матрицы являются унитарными.
  • Унитарные матрицы всегда являются квадратными матрицами .
  • Все единичные матрицы диагонализуемы, то есть могут быть преобразованы в диагональные матрицы.
  • Абсолютное значение определителя единичной матрицы всегда равно 1.

\begin{vmatrix} det(U) \end{vmatrix} = 1

  • Тождественная матрица является унитарной матрицей.
  • для всех

    n

    , набор всех единичных матриц

    n\times n

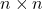
    при операции матричного произведения они образуют группу, называемую единичной группой.

  • Так что умножение двух единичных матриц одного порядка дает еще одну единичную матрицу.
  • Модуль всех собственных значений (или собственных значений) единичной матрицы всегда равен 1.

\begin{vmatrix} \lambda \end{vmatrix} = 1

  • Собственные пространства матрицы этого типа ортогональны.

Оставьте комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Прокрутить вверх